AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Ex 10(a)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(a) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 10 అవకలజాల అనువర్తనాలు Exercise 10(a)

అభ్యాసం – 10 (ఎ)

1.  కింది ప్రమేయాలకు ఎదురుగా సూచించిన x, Δx విలువలకు Δy, yలను కనుక్కోండి.

i) y = x² + 3x + 6, x = 10, Δx = 0.01 (T.S Mar. ’15, ’14, ’11, ’05)
సాధన:
Δy = f(x + Δx) – f(x)
= f(10.01) – f(10)
= [(10.01)² + 3(10.01) + 6] – [10² + 3(10) + 6]
= 100.2001 + 30.03 + 6 – 100 – 30 – 6
= 0.2001 + 0.03
= 0.2301
y = x² + 3x + 6
dy = (2x + 3) dx
= (2.10 + 3) (0.01) = 0.23

ii) y = e^x + x, x = 5, Δx = 0.02
సాధన:
Δy = f(x + Δx) – f(x)
= f(5 + 0.02) – f(5)
= f(5.02) – f(5)
= e^5.02 – e⁵ – 5
= e^5.02 – e⁵ + 0.02
= e⁵ (e^0.02 – 1) + 0.02
dy = f'(x) Δx = (e^x + 1) Δx
= (e⁵ + 1)(0.02)

iii) y = 5x² + 6x + 6, x = 2, Δx = 0.001
సాధన:
Δy = f(x + Δx) – f(x)
= f(2 + 0.001) – f(2)
= f(2.001) – f(2)
= 5(2.001)² + 6(2.001) + 6(5(2)² + 6(2) + 6)
= 20.0200 + 12.0060 + 6 – 20 – 12 – 6
= 0.026005
dy = f'(x) Δx = (10x + 6) Δx
= (26) (0.001) = 0.0260.

iv) y = \(\frac{1}{x+2}\), x = 8, Δx = 0.02
సాధన:
f(x) = \(\frac{1}{x+2}\) = \(\frac{1}{10}\) = 0.1000
f(x + Δx) = \(\frac{1}{x+\Delta x+2}\) = \(\frac{1}{10+0.02}\) = \(\frac{1}{10.02}\) = 0.0998
Δy = f(x + Δx) – f(x)
Δy = f(x + Δx – f(x))
= \(\frac{1}{x+\Delta x+2}\) – \(\frac{1}{x+2}\) = \(\frac{1}{10.02}\) – \(\frac{1}{10}\)
= 0.0998 003992 – 0.1000
= -0.0001996
dy = f'(x)Δx = \(\frac{-1}{(x+2)^2}\)Δx
= \(\frac{-1}{100}\)(0.002) = -0.0002

v) y = cos x, x = 60°, Δx = 1°
సాధన:
Δy = f(x + Δx) – f(x)
= cos (x + Δx) – cos x
= cos (60° + 1°) – cos 60°
= cos 61° – cos 60°
= 0.4848 – \(\frac{1}{2}\)
= 0.4848 – 0.5
= -0.0152
dy = f'(x) Δx
= -sin x Δx
= -sin 60°(1°) = \(\frac{-\sqrt{3}}{2}\)(0.0174)
= -(0.8660) (0.0174) = – 0.0151.

II.

1. కింది వాటికి ఉజ్జాయింపు విలువలు కనుక్కోండి.

i) \(\sqrt{82}\)
సాధన:
82 = 81 + 1 = 81(1 + \(\frac{1}{81}\))
∴ x = 8, Δx = -0.2, f(x) = \(\sqrt{x}\)
dy = f'(x). Δx = \(\frac{1}{2 \sqrt{x}}\) . Δx = \(\frac{1}{2 \sqrt{81}}\) . 1
= \(\frac{1}{18}\) = 0.0555
Δy = f(x + δx) – f(x) ≈ dy
f(x + δx) f(x) ≈ f(x) + dy
= \(\sqrt{81}\) + 0.0555
= 9 + 0.0555
i.e., \(\sqrt{82}\) = 9.0555 = 9.056

ii)
\(\sqrt[3]{65}\)
సాధన:
x = 64, Δx = 1, f(x) = \(\sqrt[3]{x}\)

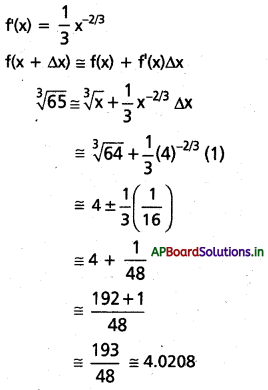
iii)
\(\sqrt{25.001}\)
సాధన:
x = 25
Δx = 0.001
f(x) = \(\sqrt{x}\)
dy = f'(x) Δx
= \(\frac{1}{2 \sqrt{x}}\)Δx = \(\frac{1}{2 \sqrt{25}}\)(0.001) = \(\frac{0.001}{10}\)
= 0.0001

f(x + Δx) \(\cong\) f(x) + dy
\(\cong\) \(\sqrt{25}\) + 0.0001
\(\sqrt{25}\) 5.0001

iv) \(\sqrt[3]{7.8}\)
సాధన:
x = 8, Δx = -0.2, f(x) = \(\sqrt[3]{x}\)
dy = f'(x). Δx
= \(\frac{1}{3} x^{-2 / 3}\) . Δx = \(\frac{1}{3 x^{2 / 3}}\) . Δx
dy = \(\frac{1}{3(8)^{2 / 3}}\) (-0.2)
= –\(\frac{0.2}{3 \times 4}\) = –\(\frac{0.2}{12}\) = -0.0166
f(x + δx) – (x) \(\simeq\) dy
f(x + δx) \(\simeq\) f(x) + dy
= \(\sqrt[3]{8}\) – 0.0166
= 2 – 0.01 66
∴ \(\sqrt[3]{7.8}\) = 1.9834

v) sin (62°)
సాధన:
x = 60°, Δx = 2°, f(x) = sin x
dy = f(x) Δx
= cosx Δx
= cos 60° Δx
= \(\frac{1}{2}\left(2^{\circ}\right)\)
= \(\frac{1}{2}\)(0.0174) = 0.0174
f(x + Δx) \(\cong\) f(x) + dy
\(\cong\) sin 60° + 0.01 74
\(\cong\) \(\frac{\sqrt{3}}{2}\) + 0.0174
\(\cong\) 0.8660 + 0.01 74
\(\cong\) 0.8834

vi) cos (60° 5′)
సాధన:
x = 60°, Δx = 5′
= \(\frac{5}{60}\) × \(\frac{\pi}{180}\) = \(\frac{\pi}{2160}\)
= 0.00143
f(x) = cos x
dy = f'(x)Δx = -sin x Δx
= -sin 60° (0.001453)
= \(\frac{-\sqrt{3}}{2}\)(0.001453)
= – 0.8660 (0.001453)
= -0.001258
f(x + Δx) \(\cong\) f(x) + dy
\(\cong\) cos x + dy
\(\cong\) cos 60° + 0.001258
\(\cong\) 0.5 – 0.001258
\(\cong\) 0.4987.

vii) \(\sqrt[4]{17}\)
సాధన:
x = 16, Δx = 1
f(x) = \(\sqrt[4]{x}\) = \(x^{\frac{1}{4}}\)

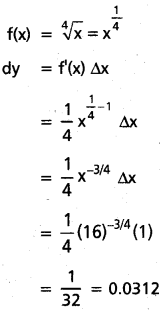
f(x + Δx) f(x) \(\cong\) f(x) + dy
\(\cong\) \(\sqrt[4]{x}\) + 0.0312
\(\cong\) 2 + 0.0312
\(\cong\) 2.0312

ప్రశ్న 2.
ఒక చతురస్ర భుజంలో పెరుగుదల 4% అయితే ఆ చతురస్రపు వైశాల్యంలో ఉజ్జాయింపు పెరుగుదల శాతాన్ని కనుక్కోండి.
సాధన:
చతురస్రం భుజం పొడవు x, వైశాల్యం A = x² అనుకుంటే
ఇచ్చినది \(\frac{\Delta x}{x}\) × 100 = 4
A = x²
ΔA = 2x Δx
\(\frac{\Delta A}{A}\) × 100 = \(\frac{2 x \Delta x}{x^2}\) × 100
= \(\frac{2 \Delta x}{x}\) × 100
= 2(4)
= 8.

ప్రశ్న 3.
ఒక గోళ వ్యాసార్థం 14 సెం.మీ.గా కొలిచారు. తరవాత ఈ వ్యాసార్థం కొలవడంలో 0.02 సెం.మీ. దోషం ఉన్నట్లుగా గమనించారు. గోళ ఉపరితల వైశాల్యంలో ఉజ్జాయింపు దోషాన్ని కనుక్కోండి.
సాధన:
గోళ ఉపరితల వైశాల్యం 5 అనుకుంటే
r = 14, Δr = 0.02
s = 4πr²
Δs = 4π 2r Δr
Δs = 8π (14) (0.02)
= 2.24π
= 2.24 (3.14)
= 7.0336.

ప్రశ్న 4.
ఒక గోళ వ్యాసం 40 సెం.మీ.గా కొలిచారు. దీనిని కొలవడంలో 0.02 సెం.మీ. దోషం ఉంటే గోళపు ఘనపరిమాణం, ఉపరితల వైశాల్యాలలో ఉజ్జాయింపు దోషాలను కనుక్కోండి. సాధన. గోళపు ఘనపరిమాణం అనుకొనుము.
సాధన:
గోళపు ఉపరితల వైశాల్యం v అనుకుంటే
v = \(\frac{4}{3} \pi r^3\) = \(\frac{4 \pi}{3}\left[\frac{\mathrm{d}}{2}\right]^3\)
= \(\frac{4 \pi}{3} \frac{d^3}{8}\)
= \(\frac{\pi \mathrm{d}^3}{6}\)
Δv = \(\frac{\pi}{6}\)3d² Δd
= \(\frac{\pi}{2}\)(40)²(0.02)
= π(1600)(0.01)
= 16π.
గోళపు ఉపరితల వైశాల్యం 5 అనుకుంటే
s = \(4 \pi\left[\frac{\mathrm{d}}{2}\right]^2\)
s = \(4 \pi \frac{d^2}{4}\)
s = πd²
Δs = π2d Δd
= π2(40) (0.02)
= 1.6π

ప్రశ్న 5.
గురుత్వ స్థిరాంకం g, లోలకం పొడవు l, డోలనావర్తన కాలం t ల మధ్య సంబంధం t = \(2 \pi \sqrt{\frac{l}{g}}\). lను గణించడంలో దోష శాతం 1 అయితే tలో ఉజ్జాయింపు దోష శాతాన్ని కనుక్కోండి.
సాధన:
T = \(2 \pi \sqrt{\frac{l}{g}}\)
log t = log (2π) + \(\frac{1}{2}\){(log (l) – log g)

∴ g లో దోషము = -0.02% (లేదా)
g లో దోష శాతము = -0.02