AP Inter 1st Year Maths 1B Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Ex 8(e)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Exercise 8(e) will help students to clear their doubts quickly.

AP Inter 1st Year Maths 1B Solutions Chapter 8 అవధులు, అవిచ్ఛిన్నత Exercise 8(e)

అభ్యాసం – 8 (ఇ)

I.

f(x) = 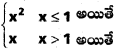ద్వారా నిర్వచితమైన ప్రమేయం f, R పై అవిచ్ఛిన్నమా ? [May ‘ 11]
సాధన:

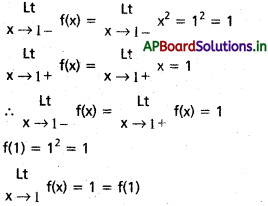
f ప్రమేయము x = 1 వద్ద అవిచ్ఛిన్నము.
f ప్రమేయము R మీద అవిచ్ఛిన్నము.

ప్రశ్న 2.
f(x) = 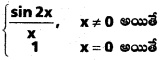ద్వారా నిర్వచితమైన ప్రమేయం f, 0 పై అవిచ్ఛిన్నామా ? [May ’12]
సాధన:
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\frac{\sin 2 x}{x} \) = 2
f(0) = 1
\(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) f(x) ≠ f(0)
f వద్ద అవిచ్ఛిన్నము కాదు.

ప్రశ్న 3.
f(x) = [cos (x¹⁰ + 1)]^1/3, x ∈ R ప్రమేయమని చూపండి.
సాధన:
ప్రతి X ∈ R కు cos x అవిచ్ఛిన్నము.
∴ ప్రతి X ∈ R దత్త ప్రమేయము అవిచ్ఛిన్నము.

II.

ప్రశ్న 1.
క్రింది ప్రమేయానికి 2 వద్ద అవిచ్ఛిన్నతను పరిశీలించండి.

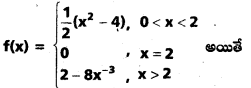
సాధన:

f(x) ప్రమేయము 2 వద్ద విచ్ఛిన్నం.

ప్రశ్న 2.

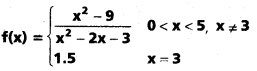
ద్వారా నిర్వచితమైన ప్రమేయం బిందువు 3 వద్ద అవిచ్ఛిన్నమేమో చూడండి. [A.P Mar. ’15, 14, ’13]
సాధన:

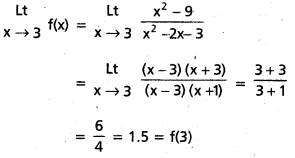
∴ f(x) ప్రమేయము x = 3 వద్ద అవిచ్ఛిన్నం.

ప్రశ్న 3.
f(x) = \(\frac{\mathrm{x}-|\mathrm{x}|}{\mathrm{x}}\) (x ≠ 0) ద్వారా నిర్వచితమైన ప్రమేయం f, R – {0} పై అవిచ్ఛిన్నం అని చూపండి.
సాధన:
సందర్భం (i) : a > 0 |a| = a

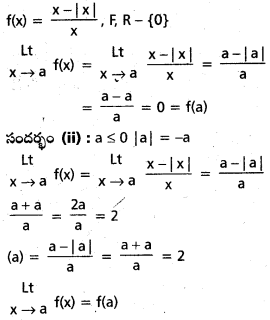
x = 0, ప్రమేయము f(a) నిర్వచించలేము
f(x) ప్రమేయము ‘0’ వద్ద విచ్ఛిన్నం
∴ f(x) ప్రమేయము R – {0} వద్ద అవిచ్ఛిన్నం.

ప్రశ్న 4.
ప్రమేయం f, f(x) = 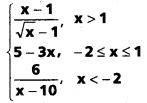తో నిర్వచితమైతే f అవిచ్ఛిన్నతను చర్చించండి.
సాధన:
సందర్భం (i) : x = 1


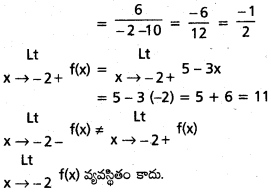
f(x) ప్రమేయము x = -2 వద్ద విచ్ఛిన్నము.

ప్రశ్న 5.
ప్రమేయము f, R పై
తో నిర్వచితమైన అవిచ్ఛిన్న ప్రమేయమైతే k విలువలు కనుక్కోండి. [T.S Mar. ’15]
సాధన:
\(\underset{\mathbf{x} \rightarrow 1-}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 1-}{\text { Lt }}\) 2 = 2
\(\underset{\mathbf{x} \rightarrow 1+}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 1+}{\text { Lt }}\) (k²x – k) = k² – k
f(x). ప్రమేయము X = 0 వద్ద అవిచ్ఛిన్నం.
\(\underset{\mathbf{x} \rightarrow 1-}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 1+}{\text { Lt }}\) f(x)
2 = k² – k
k² – k – 2 = 0
(k – 2) (k + 1) = 0
k = 2 లేదా -1

ప్రశ్న 6.
‘sin x’, ‘cos X’ ప్రమేయాలు R పై అవిచ్ఛిన్నమని చూపండి.
సాధన:
i) a ∈ R అనుకొందాం.
\(\underset{\mathbf{x} \rightarrow a}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow a}{\text { Lt }}\) sin x = sin a = f(a)
∴ f ప్రమేయము a వద్ద అవిచ్ఛిన్నం.

ii) a ∈ R అనుకొందాం.
\(\underset{\mathbf{x} \rightarrow a}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow a}{\text { Lt }}\) cos x = cos a = f(a)
cos x = cos a = f(a)
∴ f ప్రమేయము a వద్ద అవిచ్ఛిన్నం.

III.

ప్రశ్న 1.

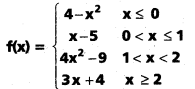
ద్వారా నిర్వచితమైన ప్రమేయం 0, 1, 2 బిందువుల వద్ద అవిచ్ఛిన్నమో చూడండి.
సాధన:
i) \(\underset{\mathbf{x} \rightarrow x}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) 4 – x² = 4 – 0 = 4 = f(0)
∴ f(x) ప్రమేయము X = 0 వద్ద అవిచ్ఛిన్నము.

ii) \(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 1}{\text { Lt }}\) (x – 5) – 1 – 5 = -4 = f(0)
∴ f(x) ప్రమేయము x = 1 వద్ద అవిచ్ఛిన్నము.

iii) \(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 2}{\text { Lt }}\) 3x + 4 = 3.2 + 4
= 6 + 4 = 10 = f(2)
∴ f(x) ప్రమేయము x = 2 వద్ద అవిచ్ఛిన్నము.

ప్రశ్న 2.

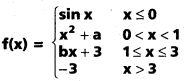
అయ్యేటట్లు నిర్వచితమైన ప్రమేయం R అవిచ్ఛిన్నం అయ్యే వాస్తవ స్థిరసంఖ్య a, b ను కనుక్కోండి. [May ’13]
సాధన:
\(\underset{\mathbf{x} \rightarrow 0+}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) (x² + a) = 0 + a = a
\(\underset{\mathbf{x} \rightarrow 0-}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 0}{\text { Lt }}\) sin x = 0
f(x) ప్రమేయము R మీద అవిచ్ఛిన్నం.
కనుక LHS = RHS ⇒ a = 0
\(\underset{\mathbf{x} \rightarrow 3+}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\) -3 = -3
\(\underset{\mathbf{x} \rightarrow 3-}{\text { Lt }}\) f(x) = \(\underset{\mathbf{x} \rightarrow 3}{\text { Lt }}\) (bx + 3) = 3b + 3
f(x) ప్రమేయము మీద అవిచ్ఛిన్నం.
LHS = RHS
3b + 3 = -3
3b = 6 b = -2

ప్రశ్న 3.
a, b లు వాస్తవ స్థిరాంకాలు అయితే ప్రమేయం

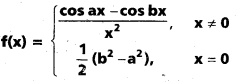
0 వద్ద అవిచ్ఛిన్నం అని చూపండి.
సాధన:

= \(\frac{2(b+a)}{2} \frac{(b-a)}{2}\) = \(\frac{\mathrm{b}^2-\mathrm{a}^2}{2}\)
f(0) = \(\frac{b^2-a^2}{2}\) కనుక \(\) f(x) = f(0)
∴ f(x) ప్రమేయము x = 0 వద్ద అవిచ్ఛిన్నం.