Andhra Pradesh BIEAP AP Inter 1st Year Physics Study Material 10th Lesson Mechanical Properties of Solids Textbook Questions and Answers.
AP Inter 1st Year Physics Study Material 10th Lesson Mechanical Properties of Solids
Very Short Answer Questions
Question 1.
State Hooke’s law of elasticity.
Answer:
“Within the elastic limit stress directly proportional to the strain”.
Stress ∝ strain
Stress = k × strain
k = \(\frac{\text { Stress }}{\text { Strain }}\)
Where k is the modulus of elasticity.
Question 2.
State the units and dimensions of stress.
Answer:
- Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{A}\)
S.l units → N/m2 (or) Pascal - Dimensional formula
Stress = \(\frac{\mathrm{MLT}^{-2}}{\mathrm{~L}^2}\) = [ML-1T-2].
![]()
Question 3.
State the units and dimensions of modulus of elasticity.
Answer:
Modulus of elasticity (k) = \(\frac{\text { Stress }}{\text { Strain }}\)
Units → N/m2 (or) Pascal
Dimensional formula → [ML-1T-2]
Question 4.
State the units and dimensions of Young’s modulus.
Answer:
Young’s modules (y) = \(\frac{\text { LongitudinalStress }}{\text { Longitudinal Strain }}=\frac{\frac{F}{A}}{\frac{e}{L}}\)
Units → N/m2 (or) Pascal
Dimensional formula → [ML-1T-2]
Question 5.
State the units and dimensions of modulus of rigidity.
Answer:
Modulus of rigidity (G) = \(\frac{F}{A \theta}=\frac{\text { Shearing Stress }}{\text { Shearing Strain }}\)
Units → N/m2 (or) Pascal
Dimensional formula → [ML-1T-2].
Question 6.
State the units and dimensions of Bulk modulus.
Answer:
Bulk modulus (B) = \(\frac{\text { Bulk Stress }}{\text { Bulk Strain }}=\frac{-P V}{\Delta V}\)
Units → N/m2 (or) Pascal
Dimensional formula → [ML-1T-2].
![]()
Question 7.
State the examples of nearly perfect elastic and plastic bodies.
Answer:
- Nearly perfect elastic bodies are quartz fibre.
- Nearly perfect plastic bodies are dough and day.
Short Answer Questions
Question 1.
Define Hooke’s Law of elasticity, proportionality, permanent set and breaking stress.
Answer:
Hooke’s law : “With in the elastic limit stress is directly proportional to the strain”.
Stress ∝ strain
Stress = k × strain
Where k is modulus of elasticity.
Proportionality limit: The maximum stress developed in a body till it obeys Hookes law is called proportionality limit.
Permanent Set : Permanent deformation produced when a body is stretched beyond its elastic limit.
Breaking stress : The maximum stress a body can bear before it breaks.
Question 2.
Define modulus of elasticity, stress, strain and Poisson’s ratio.
Answer:
Modulus of elasticity : It is the ratio stress applied on a body to the strain produced in the body.
k = \(\frac{\text { Stress }}{\text { Strain }}\)
S.I unit → N/m2 (or) Pascal
Stress : When a body is subjected to an external force, the force per unit area is called stress.
Stress = \(\frac{\text { Force }}{\text { Area }}=\frac{F}{A}\)
S.I unit → N/m2 (or) Pascal
Strain : When deforming forces act on a body, the fractional deformation produced in the body. It has no units
Poisson’s ratio (σ) : The ratio between lateral strain to longitudinal strain of a body is called poisson’s ratio.
σ = \(\frac{\text { Lateral Strain }}{\text { Longitudinal Strain }}=\frac{\frac{-\Delta \mathrm{r}}{\mathrm{r}}}{\frac{\Delta \mathrm{L}}{\mathrm{L}}}\)
![]()
Question 3.
Define Young’s modulus. Bulk modulus and Shear modulus.
Answer:
Young’s modulus (y) : With in the elastic limit, the ratio of longitudinal stress to longitudinal strain is called young’s modulus.
y = \(\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}=\frac{\frac{F}{A}}{\frac{e}{L}}\)
y = \(\frac{\mathrm{FL}}{\mathrm{A} \cdot \mathrm{e}}\)
S.I unit → N/m2 (or) Pascal
Bulk modulus (B) : With in the elastic limit, it is defined as the ratio of Bulk stress to Bulk strain
B = \(\frac{\text { Bulk Stress }}{\text { Bulk Strain }}\)
B = \(\frac{\frac{\mathrm{F}}{\mathrm{A}}}{\frac{-\Delta \mathrm{V}}{\mathrm{V}}}=\frac{-\mathrm{PV}}{\Delta \mathrm{V}}\) (∵ -ve sign indicates volume decreases)
S.I unit → N/m2 (or) Pascal
Rigidity modulus (G) : With in the elastic limit, it is defined as the ratio of shearing stress to shearing strain.
G = \(\frac{\text { Shearing Stress }}{\text { Shearing Strain }}\)
G = \(\frac{\frac{F}{A}}{\theta}=\frac{F}{A \theta}\)
S.I unit → N/m2 (or) Pascal
Question 4.
Define stress and explain the types of stress. [T.S. Mar. 16]
Answer:
Stress : The restoring force per unit area is called stress
∴ Stress = \(\frac{\text { Restoring Force }}{\text { Area }}=\frac{F}{A}\)
Stress is classified into three types.
- Longitudinal stress
- Volume (or) Bulk stress
- Tangential (or) shearing stress
1. Longitudinal stress (or) Linear stress : When a normal stress changes the length of a body, then it is called longitudinal stress.
Longitudinal stress = \(\frac{F}{A}\)
2. Volume (or) Bulk stress : When a normal stresschanges the volume of a body, then it is called volume stress.
Volume stress = \(\frac{\text { Force }}{\text { Area }}\) = pressure.
3. Tangential (or) shearing stress : When the stress is tangential to the surface due to the application of forces parallel to the surface, then the stress is called tangential stress.
Tangential stress = \(\frac{F}{A}\).
![]()
Question 5.
Define strain and explain the types of strain.
Answer:
Strain : It is the ratio of change in dimension to its original dimension.
Strain = \(\frac{\text { Changes in dimension }}{\text { Original dimension }}\)
Strain is of three types.
1. Longitudinal strain : It is the ratio of change in length to its original length.
Longitudinal strain = \(\frac{\text { Changes in length }}{\text { Original length }}=\frac{e}{L}\)
2. Shearing strain (or) Tangential strain : When simultaneous compression and extension in mutually perpendicular direction takes place in a body, the change of shape it under goes, is called shearing strain.
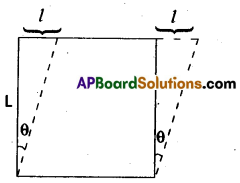
Shearing strain (θ) = \(\frac{1}{L}\)
3. Bulk (or) volume strain : It is the ratio of change in volume to its original volume is called bulk strain. It is called Bulk (or) volume strain.
Bulk strain = \(\frac{\text { Change in Volume }}{\text { Original Volume }}=\frac{\Delta V}{V}\)
Question 6.
Define strain energy and derive the equation for the same. [Mar. 14]
Answer:
The potential energy stored in a body when stretched is called strain energy.
Let us consider a wire of length L and cross – sectional area A. Let x be the change in length of the wire by the application of stretching force F.

Strain energy per unit volume = \(\frac{1}{2} \times \frac{F}{A} \cdot \frac{x}{L}\)
= \(\frac{1}{2}\) × stress × strain.
![]()
Question 7.
Explain why steel is preferred to copper, brass, aluminium in heavy-duty machines and in structural designs.
Answer:
The elastic behavior of materials plays an important role in everyday life. Designing of buildings, the structural design of the columns, beams and supports require knowledge of strength of material used. The elasticity of the material is due to stress developed with in the body, when extenal force acts on it. A material is of more elastic nature if it develops more stress (or) restoring force. Steel develops more stress than copper, brass, aluminium for same strain. So steel is more elastic.
y = \(\frac{\text { Stress }}{\text { Strain }}\)
Question 8.
Describe the behaviour of a wire under gradually increasing load. [A.P. – Mar. ’18, ’16, ’15; TS – Mar. ’18, ’15, ’13]
Answer:
When the load is increased in steps, a graph is drawn between stress on y-axis and corresponding strain on x-axis.
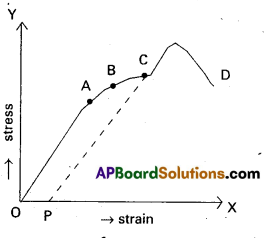
1. Proportionality limit : In the linear position OA, stress is proportional to strain, i.e. Hookes law is obeyed by the wire upto point A. The graph is a straight lint. When ever the stretching force at A is removed, the wire regains its original length.
A is called proportionality limit.
2. Elastic limit : In the graph B is the elastic limit.
Through the wire doesnot obey Hooke’s law at B. The wire regains its original length after removing the stretching force at B. upto point B the wire is under elastic behaviour.
3. Permanent set (or) yield point: In the graph c is the yield point. If the stretching force at c is removed, the wire doesnot regain its original length and the length of the wire changes permanently. In this position the wire flows like a viscous liquid. After the point c, the wire is under plastic behavior, c is called permanent set (or) yield point.
4. Breaking point: When the stress increased, the wire becomes thinner and thinner. When the stress increases to a certain limit the wire breaks. The stress at which the wire breaks is called breaking stress and the point D is called breaking point.
5. Elastic fatigue : The state of temperary loss of elastic nature of a body due to continuous strain is called elastic fatigue. When a body is subjected to continuous strain with in the elastic limit, it appears to have lost Hastic property temporarily to some extent and becomes weak.
![]()
Question 9.
Two identical solid balls, one of ivory and the other of wet-day are dropped from the same height onto the floor. Which one will rise to greater height after striking the floor and why ?
Answer:
Ivory ball rise to greater height after striking the floor. The ivory ball regain its original shape after striking the floor. The elastic property of ivory ball is more. Where as wet-day ball does not regain its original shape after striking the floor.
So wet-day ball acts like plastic body.
Question 10.
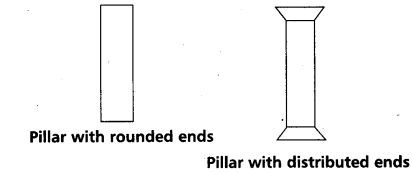
While constructing buildings and bridges a pillar with distributed ends is preferred to a pillar with rounded ends. Why ?
Answer:
Use of pillars (or) columns is also very common in buildings and bridges. A pillar with rounded ends supports less load than that with a distributed shape at the ends. The precise design of a bridge (or) a building has to take into account the conditions under which it will function, the cost and long period, reliability of usable materials.
Question 11.
Explain why the maximum height of a mountain on earth is approximately 10 km ?
Answer:
The maximum height of a mountain on earth is 10 km, can also be provided by considering the elastic properties of rocks. A mountain base is not under uniform compression and this provides some shearing stress to rocks under which they can flow. The stress due to all the material on the top should be less than the critical shearing stress at which the rocks flow.
At the bottom of a mountain of height h, the force per unit area due to the weight of the mountain is hρg. Where ρ is the density of the mountain. The material at the bottom experiences this force in the vertical direction and the sides of the mountain are free.
There is a shear component, approximately hρg itself.
Elastic limit for 3 typical rock is 30 × 107 N/m2
hρg = 30 × 107 (ρ = 3 × 103 kg/m3)
h = \(\frac{30 \times 10^7}{3 \times 10^3 \times 10}\)
h = 10 km.
![]()
Question 12.
Explain the concept of Elastic Potential Energy in a stretched wire and hence obtain the expression for it.
Answer:
“When a wire is put under a tensile stress, work is done against the inter-atomic forces. The work is stored in the wire in the form of elastic potential energy”.
Expression for elastic potential energy : Consider a wire of length L and area of cross section A is subjected to a deforming force F along the length of the wire. Let the length of the wire is elongated by l.
Young’s modulus (y) = \(\frac{\mathrm{FL}}{\mathrm{Al}}\)
F = \(\frac{\mathrm{yAl}}{\mathrm{L}}\) ……………. (1)
Work done due to further elongation of small length dl
Work done (dw) = F × dl = (\(\frac{\mathrm{yAl}}{\mathrm{L}}\))dl ……………… (2)
Total work done in increasing the length of the wire from L to (L + l)
w = \(\int_0^1 \frac{\mathrm{yAl} }{\mathrm{L}} \mathrm{dl}=\frac{\mathrm{yA}}{2} \times \frac{l^2}{\mathrm{~L}}\)
w = \(\frac{1}{2} \times \mathrm{y} \times\left(\frac{l}{\mathrm{~L}}\right)^2 \times \mathrm{Al}\)
= \(\frac{1}{2}\) y × stress2 × volume of the wire
w = \(\frac{1}{2}\) × stress × strain × volume of the wire.
This work is stored in the wire in elastic potential energy (u).
Long Answer Question
Question 1.
Define Hooke’s law of elasticity and describe an experiment to determine the Young’s modulus of the material of a wire.
Answer:
Hooke’s law : With in the elastic limit, stress is directly proportional to the strain.
Stress ∝ strain
Stress = k × strain
Where k is modulus of elasticity.
Determination of young’s modulus of the material of a wire:

Young’s Modulus of the Material of a wire
- It consists of two long straight wires of same length and same area of cross-section suspended side by side from a rigid .support.
- The wire A (reference wire) carries a metre scale M and a pan to place a weight.
- The wire B (experimental wire) carries a pan in which known weights can be placed.
- A vernier scale v is attached to a pointer at the bottom of the experimental wire B and the main scale M is fixed to the wire A.
- The weights placed in the pan, the elongation of the wire is measured by the vernier arrangement.
- The reference wire is used to compensate for any change in length that may occur due to change in room temperature.
- Both the reference and experimental wires are given an initial small load to keep the wires straight and the vernier reading is noted.
- Now the experimental wire is gradually loaded with more weights, the vernier reading is noted again.
- The difference between two vernier readings gives the elongation produced in the wire.
- Let r and L be the radius and initial length of the experimental wire. Let M be the mass that produced an elongation ∆L in the wire.
Young’s modulus of the material of the experimental wire is given by
y = \(\frac{\text { Longitudinal Stress }}{\text { Longitudinal Strain }}=\frac{\frac{\mathrm{F}}{\mathrm{A}}}{\frac{\Delta \mathrm{L}}{\mathrm{L}}}\)
y = \(\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}\)
y = \(\frac{\mathrm{MgL}}{\pi r^2 \times \Delta \mathrm{L}}\)
From above equation young’s modulus of the material of the wire is determined.
Problems
Question 1.
A copper wire of 1mm diameter is stretched by applying a force of 10 N. Find the stress in the wire.
Solution:
D = 1 m.m = 10-3m, r = \(\frac{D}{2}\) = 0.5 × 10-3 m.
F = 10 N
Stress = \(\frac{F}{A}=\frac{F}{\pi r^2}\)
= \(\frac{10}{3.14 \times\left(0.5 \times 10^{-3}\right)^2}\)
= 1.273 × 107 N/m2.
![]()
Question 2.
A tungsten wire of length 20 cm is stretched by 0.1 cm. Find the strain on the wire.
Solution:
L = 20 × 10-2 m, ∆L = 0.1 × 10-2 m
Strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}=\frac{0.1 \times 10^{-2}}{20 \times 10^{-2}}\) = 0.005.
Question 3.
If an iron wire is stretched by 1 %, what is the strain on the Wire ?
Solution:
Strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}\) = 1 %
Strain = \(\frac{1}{100}\) = 0.01
Question 4.
A brass wire of diameter 1mm and length 2 m is streched by applying a force of 20N. If the increase in length is 0.51 mm. find
(i) the stress,
(ii) the strain and
(iii) the Young’s modulus of the wire.
Solution:
D = 1 m.m, r = \(\frac{D}{2}\) = 0.5 × 10-3 m
L = 2 m, F = 20 N, ∆L = 0.51 m.m = 0.51 × 10-3 m

= 9.984 × 1010 N/m2
Question 5.
A copper wire and an aluminium wire have lengths in the ratio 3 : 2, diameters in the ratio 2 : 3 and forces applied in the ratio 4: 5. Find the ratio of increase in length of the two wires. (Ycu = 1.1 × 1011 Nm-2, YAl = 0.7 × 1011 Nm-2).
Solution:
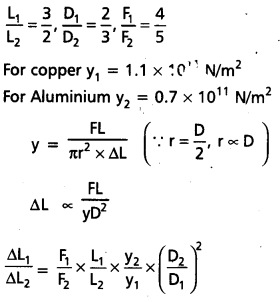
= \(\frac{4}{5} \times \frac{3}{2} \times\left(\frac{0.7 \times 10^{11}}{1.1 \times 10^{11}}\right) \times\left(\frac{3}{2}\right)^2\)
\(\frac{\Delta \mathrm{L}_1}{\Delta \mathrm{L}_2}=\frac{189}{110}\)
![]()
Question 6.
A brass wire of cross-sectional area 2 mm2 is suspended from a rigid support and a body of volume 100 cm3 is attached to its other end. If the decrease in the length of the wire is 0.11 mm, when the body is completely immersed in water, find the natural length of the wire.
(Ybrass = 0.91 × 1011 Nm-2, ρwater = 103 kg m-3).
Solution:
A = πr2 = 2 × 10-6 m2, V = 100 × 10-6 = 10-4 m3
∆L = 0.11 × 10-3 m, yBrass = 0.91 × 1011 N/m2, ρ = 103 kg/m3
y = \(\frac{M g L}{A \times \Delta L}=\frac{v \rho g L}{A \times \Delta L}\)
L = \(\frac{\mathrm{yA} \Delta \mathrm{L}}{\mathrm{v \rho g}}=\frac{0.91 \times 10^{11} \times 2 \times 10^{-6} \times 0.11 \times 10^{-3}}{10^{-4} \times 10^3 \times 9.8}\)
L = 2.04 m.
Question 7.
There are two wires of same material. Their radii and lengths are both in the ratio 1:2. If the extensions produced are equal, what is the ratio of loads ?
Solution:
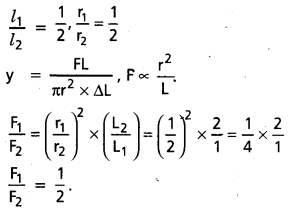
Question 8.
Two wires of different material have same lengths and areas of cross¬section. What is the ratio of their increase in length when forces applied are the same ?
(Y1 = 0.9 × 1011 Nm-2, Y2 = 3.6 × 1011 Nm-2)
Solution:
y1 = 0.9 × 1011 Nm-2
y2 = 3.6 × 1011 Nm-2
y = \(\frac{F L}{A \times \Delta L}\)
∆L ∝ \(\frac{1}{y}\)
\(\frac{(\Delta L)_1}{(\Delta L)_2}=\frac{y_2}{y_1}=\frac{3.6 \times 10^{11}}{0.9 \times 10^{11}}=\frac{4}{1}\)
![]()
Question 9.
A metal wire of length 2.5 m and area of cross-section 1.5 × 10-6 m2 is stretched through 2 mm. if its Young’s modulus is 1.25 × 1011 N.m2, find the tension in the wire.
Solution:
L = 2.5 m, A = 1.5 × 10-6 m2
∆L = 2 × 10-9 m
y = 1.25 × 1011 N.m2
y = \(\frac{\mathrm{FL}}{\mathrm{A} \Delta \mathrm{L}}\)
F = \(\frac{\mathrm{yA} \Delta \mathrm{L}}{\mathrm{L}}\)
= \(\frac{1.25 \times 10^{11} \times 1.5 \times 10^{-6} \times 2 \times 10^{-3}}{2.5}\)
F = 150 N
Question 10.
An aluminium wire and a steel wire of the same length and cross-section are joined end-to-end. The composite wire is hung from a rigid support and a load is suspended from the free end. If the increase in length of the composite wire is 1.35 mm, find the ratio of the
(i) stress in the two wires and
(ii) strain in the two wires.
(YAl = 0.7 × 1011 N.m2, YSteel = 2 × 1011 Nm2).
Solution:
YAl = 0.7 × 1011 N.m2, YSteel = 2 × 1011 Nm2
∆L1 + ∆L2 = 1.35 mm ……………… (1)

Question 11.
A 2 cm cube of some substance has its upper face displaced by 0.15 cm due to a tangential force of 0.3 N while keeping the lower face fixed, Calculate the rigidity modulus of the substance.
Solution:
L = 2 × 10-2 m, A = L2 = 4 × 10-4 m2
∆x = 0.15 × 10-2 m
F = 0.3 N
G = \(\frac{\frac{F}{A}}{\frac{\Delta x}{L}}=\frac{F L}{A \Delta x}\) (∵ θ = \(\frac{\Delta x}{L}\))
G = \(\frac{0.3 \times 2 \times 10^{-2}}{4 \times 10^{-4} \times 0.15^6 \times 10^{-2}}\)
G = 104 N/m2
![]()
Question 12.
A spherical ball of volume 1000 cm3 is subjected to a pressure of 10 Atmosphere. The change in volume is 10-2 cm3. If the ball is made of iron, find its bulk modulus.
(1 atmosphere = 1 × 105 Nm-2).
Solution:
v = 1000 cm3 = 1000 × 10-6 = 10-3 m3
p = 1 atm = 1 × 105 = 105 N/m2
-∆v = 10-2 cm3 = 10-2 × 10-6 = 10-8 m3
Bulk modulus (B) = \(\frac{-p v}{\Delta v}\)
= \(\frac{10^5 \times 10^{-3}}{10^{-8}}\)
B = 1010 N/m2.
Question 13.
A copper cube of side of length 1 cm is subjected to a pressure of 100 atmosphere. Find the change in its volume if the bulk modulus of copper is 1.4 × 1011 Nm-2. (1 atm = 1 × 105 Nm-2).
Solution:
l = 1 cm = 10-2 m
V = Volume of the cube = l3 = 1cm3
= 10-6 m3
P = 100 atm = 100 × 105 = 107 N/m2
B = 1.4 × 1011 N/m2
B = \(\frac{-P V}{\Delta V}\)
-∆V = \(\frac{P V}{B}=\frac{10^7 \times 10^{-6}}{1.4 \times 10^{11}}\)
-∆V = 0.7143 × 10-10 m3.
Question 14.
Determine the pressure required to reduce the given volume of water by 2%. Bulk modulus of water is 2.2 × 109 Nm-2.
Solution:
\(\frac{-\Delta V}{V}\) = 2 % = \(\frac{2}{100}\)
B = 2.2 × 109 Nm2
B = \(\frac{-P V}{\Delta V}\)
P = -B × \(\frac{\Delta V}{V}\)
= 2.2 × 109 × \(\frac{2}{100}\)
P = 4.4 × 107 N/m2.
![]()
Question 15.
A steel wire of length 20 cm is stretched to increase its length by 0.2 cm. Find the lateral strain in the wire if the Poisson’s ratio for steel is 0.19.
Solution:
L = 20 cm = 20 × 10-2 m
∆L = 0.2 × 10-2 m
σ = 0.19
σ = \(\frac{\text { Lateral strain }}{\text { Longitudinal strain }\left(\frac{\Delta \mathrm{L}}{\mathrm{L}}\right)}\)
Lateral strain = σ × \(\frac{\Delta L}{L}\)
= \(\frac{0.19 \times 0.2 \times 10^{-2}}{20 \times 10^{-2}}\)
= 0.0019
Additional Problems
Question 1.
A steel wire of length 4.7 m and cross-sectional area 3.0 × 10-5 m2 stretches by the same amount as a copper wire of length 3.5 m and cross-sectional area of 4.0 × 10-5 m2,
Solution:
Given, for steel wire, a1 = 3.0 × 10-5 m2, l1 = 4.7 m, ∆l1 = ∆l, F1 = F
For copper wire, a2 = 4.0 × 10-5 m2, l2 = 3.5 m, ∆l2 = ∆l, F2 = F .
Let y1, y2 be the young modulus of steel wire and copper wire respectively.
∴ y1 = \(\frac{F_1}{a_1} \times \frac{l_1}{\Delta l_2}=\frac{F}{3.0 \times 10^{-5}} \times \frac{4.7}{\Delta l}\) ………….. (i)
and y2 = \(\frac{F_2 \times l_2}{a_2 \times \Delta l_2}=\frac{F \times 3.2}{4 \times 10^{-5} \times \Delta l}\)
\(\frac{\mathrm{y}_1}{\mathrm{y}_2}=\frac{4.7 \times 4 \times 10^{-5}}{3.5 \times 3.0 \times 10^{-5}}\) = 1.8
Here y1 : y1 = 1.8 : 1.
Question 2.
Figure shows the strain-stress curve for a given material. What are (a) Young’s modulus and (b) approximate yield strength for this material ?
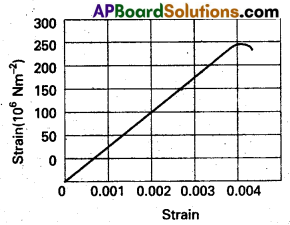
Solution:
a) From graph, for stress = 150 × 106 Nm-2 the corresponding strain = 0.002
young’s modulus y = \(\frac{\text { Stress }}{\text { Strain }}=\frac{150 \times 10^6}{0.002}\)
= 7.5 × 1010 Nm-2
b) Approximate yeild strength will be equal to the maximum stress it can substain with out crossing the elastic limit. Therefore, the approximate yeild strength
= 300 × 106 Nm-2
= 3 × 108 Nm-2
![]()
Question 3.
The stress-strain graphs for materials A and B are shown in Fig.
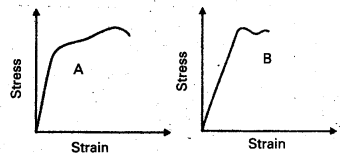
The graphs are drawn to the same scale.
a) Which of the materials has the greater Young’s modulus ?
b) Which of the two is the stronger material ?
Solution:
a) From the two graphs we note that for a given strain, stress for A is more than that of B. Hence young’s modulus (= stress/ strain) is greater for A than that of B.
b) A is stronger than B. Strength of a material is measured by the amount of stress required to cause fracture, corresponding to the point of fracture.
Question 4.
Read the following two statements below carefully and state, with reasons, if it is true or false.
a) The Young’s modulus of rubber is greater than that of steel;
b) The stretching of a coil is determined by its shear modulus.
Solution:
a) False, because for a given stress there is more strain in rubber than steel and modulus of elasticity is inversly proportional to strain.
b) True because the strecting of coil simply changes its shape without any change in the length of the wire used in the coil due to which shear modulus of elasticity is involved.
![]()
Question 5.
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in Fig. The unloaded length of steel wire is 1.5 m and that of brass Wire is 1.0 m. Compute the elongations of the steel and the brass wires.
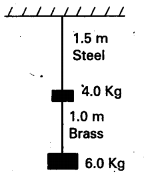
Solution:
For steel wire, total force on steel wire,
F1 = 4 + 6 = 10 kg, f = 10 × 9.8 N
l1 = 1.5 m, ∆l1 = ?, 2r1 = 0.25cm or r1 =(0.25/2)cm = 0.125 × 10-2 m
y1 = 2.0 × 1011 pa
For brass wire, F2 = 6.0 kg, f = 6 × 9.8 N
2r2 = 0.25 cm or r2 = (0.25/2) cm = 0.125 × 10-2 m,
y2 = 0.91 × 1011 pa, l2 = 1.0 m, ∆l2 = ?

Question 6.
The edge of an aluminium cube is 10 cm long. One face of the cube is firmly fixed to a verticle wall. A mass of 100 kdis then attached to the opposite face of the cube. The shear modulus of aluminium is 25 GPa. What is the vertical deflection of this face?
Solution:
A = 0.10 × 0.10 = 10-2 m2, F = mg = 100 × 10 N
Shearing strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}}=\frac{\left(\frac{\mathrm{F}}{\mathrm{A}}\right)}{\eta}\)
or ∆L = \(\frac{F L}{A \eta}\)
= \(\frac{(100 \times 10) \times(0.10)}{10^{-2} \times\left(25 \times 10^9\right)}\) = 4 × 10-7 m.
Question 7.
Four identical hollow cylindrical columns of mild steel support a big structure of mass 50,000 kg. The inner and outer radii of each column are 30 and 60 cm respectively. Assuming the load distribution to be uniform, calculate the corn pressional strain of each column.
Solution:
Load on each column, F = \(\frac{50,000}{4}\) kgwt
= \(\frac{50,000 \times 9.8}{4}\) N
A = π(r22 – r12) = \(\frac{22}{7}\)(0.60)2 – (0.30)2]
= \(\frac{22}{7}\) 0.27 m2
Compression strain = \(\frac{\frac{F}{A}}{y}=\frac{F}{A y}\)
= \(\frac{50,000 \times 9.8}{4 \times\left(\frac{22}{7} \times 0.27\right) \times 2.0 \times 10^{11}}\)
= 7.21 × 10-7.
![]()
Question 8.
A piece of copper having a rectangular cross-section of 15.2 mm × 19.1 mm is pulled in tension with 44,500 N force, producing only elastic deformation. Calculate the resulting strain?
Solution:
Here, A = 15.2 × 19.2 × 10-6 m2, F = 44,
500 N, η = 42 × 109 Nm-2
Strain = \(\frac{\text { Stress }}{\text { Modulus of elasticity }}\)
= \(\frac{\frac{F}{A}}{\eta}=\frac{F}{A \eta}=\frac{44500}{\left(15.2 \times 19.2 \times 10^{-6}\right) \times 42 \times 10^9}\)
= 3.65 × 10-3.
Question 9.
A steel cable with a radius of 1.5 cm supports a chairlift at a ski area. If the maximum stress Is not to exceed 108 N m-2, what is the maximum load the cable can support ?
Solution:
Maximum load macimum stress × area of cross-section
= 108πr2
= 108 × \(\frac{22}{7}\) × (1.5 × 10-2)2
= 7.07 × 104 N.
Question 10.
A rigid bar of mass 15 kg is supported symmetrically by three wires each 2.0 m long. Those at each end are of copper and the middle one is of iron. Determine the ratios of their diameters if each is to have the same tension.
Solution:
As each wire has same tension F, so each wire has same extansion due to mass of rigid bar. As each wire is of same length, hence each wire has same strain, if D is the diameter of wire, then
y = \(\frac{4 \mathrm{~F} / \pi \mathrm{D}^2}{\text { Strain }}\) or D2 ∝ 1/y
\(\frac{D_{\mathrm{cu}}}{\mathrm{D}_{\mathrm{iron}}}=\sqrt{\frac{\mathrm{y}_{\mathrm{iron}}}{\mathrm{y}_{\mathrm{cu}}}}\)
= \(\sqrt{\frac{190 \times 10^9}{110 \times 10^9}}=\sqrt{\frac{19}{11}}\) = 1.31.
![]()
Question 11.
A 14.5 kg mass, fastened to the end of a steel wire of unstretched length 1.0 m, is whirled in a vertical circle with an angular velocity of 2 rev/s at the bottom of the circle. The cross-sectional area of the wire is 0.065 cm2. Calculate the elongation of the wire when the mass is at the lowest point of its path.
Solution:
Here, m = 14.5 kg, l = r = 1m, v = 2 rps, A = 0.065 × 10-4 m2
Total pulling force on mass, when it is at the lowest position of the vertical circle is
F = mg + mrω2
= mg + mr4πv2
= 14.5 × 9.8 + 14.5 × 1 × 4 × (\(\frac{22}{7}\))2 × 22
= 142.1 +2291.6
= 2433.7 N
y = \(\frac{F}{A} \times \frac{l}{\Delta l}\) or ∆l = \(\frac{F l}{A y}\)
= \(\frac{2433.7 \times 1}{\left(0.065 \times 10^{-4}\right) \times\left(2 \times 10^{11}\right)}\)
= 1.87 × 10-3 m
= 1.87 mm.
Question 12.
Compute the bulk modulus of water from the following data : Initial volume = 100.0 litre, Pressure increase = 100.0 atm (1 atm = 1.013 × 105 Pa), Final volume = 100.5 litre. Compare the bulk modulus of water with that of air (at constant temperature). Explain in simple terms why the ratio is so large.
Solution:
Here, V = 100 lit = 100 × 10-3 m3, P = 100 atm = 100 × 1.013 × 105 Pa
V + ∆V = 100.5 litre or ∆V= (V + ∆V) – V
= 100.5 – 100
= 0.5 litre = 0.5 × 10-3 m3
We known that bulk modulus, B = \(\frac{\mathrm{PV}}{\Delta \mathrm{V}}\)
= \(\frac{100 \times 1.013 \times 10^5 \times 100 \times 10^{-3}}{0.5 \times 10^{-3}}\)
= 2.026 × 109 Pa
Bulk modulus of air = 1.0 × 105 Pa
\(\frac{\text { Bulk modulus of water }}{\text { Bulk modulus of air }}=\frac{2.026 \times 10^9}{1.0 \times 10^5}\)
= 2.026 × 1014.
It is so because gases are much more compressible than those of liquids. The molecules in gases are very poorly coupled to their neighbours as compared to those of gases.
![]()
Question 13.
What is the density of water at a depth where pressure is 80.0 atm, given that its density at the surface is 1.03 × 103 kg m-3 ?
Solution:
Here, P = 80.0 atm = 80.0 × 1.013 × 105 pa,
compressibility = \(\left(\frac{1}{B}\right)\) = 45.8 × 10-11 pa-1
Density of water at surface,
ρ = 1.03 × 103 kg m-3
Let p be the density of water at the given depth, if v and v’ are volumes of certain mass M of ocean water at surface and at a given

Putting this value in (i) we get
1 – \(\frac{1.03 \times 10^3}{\rho^{\prime}}\) = 3.712 × 10-3 or
ρ’ = \(\frac{1.03 \times 10^3}{1-3.712 \times 10^{-3}}\) = 1.034 × 103 kg m-3.
Question 14.
Compute the fractional change in volume of a glass slab, when subjected to a hydraulic pressure of 10 atm.
Solution:
Here, P = 10 atm = 10 × 1.013 × 105 pa,
B = 37 × 109 Nm-2
Volumetric strain = \(\frac{\Delta V}{V}=\frac{P}{B}\)
= \(\frac{10 \times 1.013 \times 10^5}{37 \times 10^9}\) = 2.74 × 10-5
∴ Fractional change in volume = \(\frac{\Delta V}{V}\)
= 2.74 × 10-5
![]()
Question 15.
Determine the volume contraction of a solid copper cube, 10 cm on an edge, when subjected to a hydraulic pressure of 7.0 × 106 Pa.
Solution:
Here, L = 10 cm = 0.10m; P = 7 × 106 pa B = 140 Gpa = 140 × 109 pa
As B = \(\frac{\mathrm{PV}}{\Delta \mathrm{V}}=\frac{\mathrm{Pl}^3}{\Delta \mathrm{V}}\) or ∆V = \(\frac{\mathrm{Pl}^3}{\mathrm{~B}}\)
= \(\frac{\left(7 \times 10^6\right) \times(0.10)^3}{140 \times 10^9}\) = 5 × 10-8 m3
= 5 × 10-2 mm3
Question 16.
How much should be pressure on a litre of water be changed to compress it by 0.10% ?
Solution:
Here, V = 1 litre = 10-3m3;
∆V/V = 0,10/100 = 10-3
B = \(\frac{P V}{\Delta V}\) or P = B \(\frac{\Delta V}{V}\)
= (2.2 × 109) × 10-3 = 2.2 × 106pa
Question 17.
Anvils made of single crystals of diamond, with the shape as shown in Fig. are used to investigate behaviour of materials under very high pressures. Flat faces at the narrow end of the anvil have a diameter of 0.50 mm, and the wide ends are subjected to a compressional force of 50,000 N. What is the pressure at the tip of the anvil ?
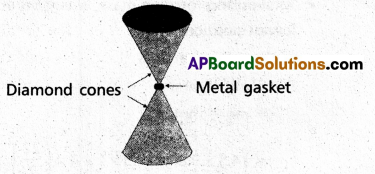
Solution:
Here, D = 0.5 mm = 0.5 × 10-3m = 5 × 10-4m
F = 50,000 N = 5 × 104N
Pressure at the tip of anvil.
P = \(\frac{F}{\pi D^2 / 4}=\frac{4 F}{\pi D^2}\)
P = \(\frac{4 \times\left(5 \times 10^4\right)}{(22 / 7) \times\left(5 \times 10^{-4}\right)^2}\) = 2.5 × 1011pa.
![]()
Question 18.
A rod of length 1.05 m having negligible mass is supported at its end by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Fig. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
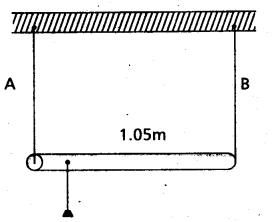
Solution:
For Steel wire A, l1 = l, A1 = 1 mm2
Y1 = 2 × 1011Nm-2
For aluminium wire B, l2 = l;
A2 = 2mm2; y2 = 7 × 1010 Nm-2
a) Let mass m be suspended from the rod at the distance × from the end where wires A is connected. Let F1 and F2 be the tension in two wires and there is equal stress in two wires, then
\(\frac{F_1}{A_1}=\frac{F_2}{A_2} \text { or } \frac{F_1}{F_2}=\frac{A_1}{A_2}=\frac{1}{2}\) …………………. (i)
Taking moment of forces about the point of suspension of mass from the rod, we have
F1x = F2 (1.05 – x) or \(\frac{1.05-x}{x}=\frac{F_1}{F_2}=\frac{1}{2}\)
or 2.10 – 2x = x or x = 0.70m = 70 cm
b) Let mass m be supended from the rod at distance × from the end where wire A is connected. Let F1 and F2 be the tension in the wires and there is equal strain in the two wires i.e.
\(\frac{F_1}{A_1 Y_1}=\frac{F_2}{A_2 Y_2}\) or \(\frac{F_1}{F_2}=\frac{A_1}{A_2} \frac{Y_1}{Y_2}\)
= \(\frac{1}{2} \times \frac{2 \times 10^{11}}{7 \times 10^{10}}=\frac{10}{7}\)
As the rod is stationary, so F1x = F2(1.05 – x)
or \(\frac{1.05-x}{x}=\frac{F_1}{F_2}=\frac{10}{7}\)
or 10 x = 7.35 – 7x
or x = 0.4324 m
x = 43.2cm.
![]()
Question 19.
A mild steel wire of length 1.0 m and cross-sectional area 0.50 × 10-2 cm2 is stretched, well within its elastic limit, horizontally between two pillars. A mass of 100 g is suspended from the mid-point of the wire. Calculate the depression at the- mid-point.
Solution:
Refer the figure, let x be the depression at the mid point i.e CD = x
In fig. AC = CB = Z = 0.5m
m = 100g = 0.100 kg
AD = BD = (l2 + x2)1/2
Increase in length, ∆l = AD + DB – AB
= 2 AD – AB
= 2 (l2 + x2)1/2 – 2l
= 2l(1 + \(\frac{x^2}{l^2}\))1/2 – 2l
= 2l (1 + \(\frac{x^2}{2 l^2}\)) – 2l = \(\frac{x^2}{l}\)
Strain = \(\frac{\Delta l}{2 l}=\frac{x^2}{2 l^2}\)
If T is the tension in the wire, then 2T cos θ
= mg or T = \(\frac{\mathrm{mg}}{2 \cos \theta}\)
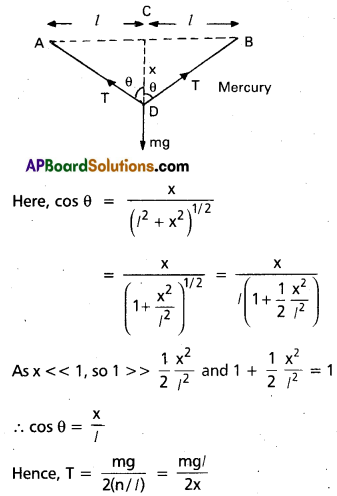

Question 20.
Two strips of metal are riveted together at their ends by four rivets, each of diameter 6.0 mm. What is the maximum tension that can be exerted by the riveted strip if the shearing stress on the rivet is not to exceed 6.9 × 107 Pa ? Assume that each rivet is to carry one quarter of the load.
Solution:
Here, r = 6/2 = 3mm = 3 × 10-3 m, max.
stress = 6.9 × 107 Pa
Max . load on a rivet = Max stress × area of cross section
= 6.9 × 107 × (22/7) × (3 × 10-3)2
∴ Maximum tension
= 4 (6.9 × 107 × \(\frac{22}{7}\) × 9 × 10-6)
= 7.8 × 103N.
![]()
Question 21.
The Marina trench is located in the Pacific Ocean, and at one place it is nearly eleven km beneath the surface of water. The water pressure at the bottom of the trench is about 1.1 × 108 Pa. A steel ball of initial volume 0.32 m3 is dropped into the ocean and falls to the bottom of the trench. What is the change in the volume of the ball when it reaches to the bottom ?
Solution:
Here, P = 1.1 × 108 Pa, V = 0.32 m3,
B = 16 × 1011Pa
∆V = \(\frac{\mathrm{PV}}{\mathrm{B}}\)
= \(\frac{\left(1.1 \times 10^8\right) \times 0.32}{1.6 \times 10^{11}}\)
= 2.2 × 10-4m3
Textual Examples
Question 1.
A structural steel rod has a radius of 10 mm and a length of 10 m. A 100 KN force stretches it along its length. Calculate (a) stress, (b) elongation, and (c) strain on the rod. Young’s modulus, of structural steel ¡s 2.0 × 1011 Nm2.
Answer:
a) Given Stress = \(\frac{F}{A}=\frac{F}{\pi r^2}\)
= \(\frac{100 \times 10^3 \mathrm{~N}}{3.14 \times\left(10^{-2} \mathrm{~m}\right)^2}\) = 3.18 × 108 Nm-2
b) The elongation
∆L = \(\frac{(\mathrm{F} / \mathrm{A}) \mathrm{L}}{\mathrm{Y}}\)
= \(\frac{\left(3.18 \times 10^8 \mathrm{Nm}^2\right)(1 \mathrm{~m})}{2 \times 10^{11} \mathrm{Nm}^{-2}}\)
= 1.59 × 10-3 m
= 1.59 mm
c) The strain is given by
Strain = ∆L/L = (1.59 × 10-3) km
= 1.59 × 10-3 = 0.16%
Question 2.
A copper wire of length 2.2 m and a steel wire of length 1.6 m, both of diameter 3.0 mm, are connected end to end. When stretched by a load, the net elongation is found to be 0.70 mm. Obtain the load applied.
Answer:
From y = \(\frac{\sigma}{\varepsilon}\)
we have stress = strain × Young’s modulus.
W/A = Yc × (∆Lc/Lc) = Ys × (∆Ls/Ls)
where the subscripts c and s refer to copper and stainless steel respectively,
∆Lc/∆Ls = (Ys/Ys) () (Lc/Ls)
Given Lc = 2.2 m, Ls = 1.6 m,
Yc = 1.1 × 1011 N.m-2 and Ys = 2.0 × 1011 N.m-2.
∆Lc/∆Ls = \(\frac{2.0 \times 10^{11}}{1.1 \times 10^{11}}=\frac{2.2}{1.6}\) = 2.5
∆Lc + ∆Ls = 7.0 × 10-4 m
Solving the above equations,
∆Lc = 5.0 × 10-4 m and ∆Ls = 2.0 × 10-4 m.
∴ W = (A × Yc × ∆Lc)Lc
= π(1.5 × 10-3)2 × \(\left[\frac{\left(5.0 \times 10^{-4} \times 1.1 \times 10^{11}\right)}{2.2}\right]\) = 1.8 × 102 N.
![]()
Question 3.
In a human pyramid in a circus, the entire weight of the balanced group is supported by the legs of a performer who is lying on his back (as shown in Fig.) The combined mass of all the persons performing the act and the tables, planks etc. involved is 280 kg. The mass of the performer lying on his back at the bottom of the pyramid is 60 kg. Each thighbone (femur) of this performer has a length of 50 cm and an effective radius of 2.0 cm. Determine the amount by which each thighbone gets compressed under the extra load.

Answer:
Total mass of all the performers, tables, plaques = 280 kg
Mass of the performer = 60 kg
Mass supported by the legs of the performer at the bottom of the pyramid = 280 – 60
= 220 kg
Weight of this supported mass = 220 kg wt.
= 220 × 9.8 N = 2156 N
Weight supported by each thighbone of the performer = \(\frac{1}{2}\) (2156) N = 1078 N.
The Young’s modulus for bone is Y = 9.4 × 109 Nm-2 (compressive)
Length of each thighbone L = 0.5 m the radius of thigbone = 2.0 cm
Thus the cross-sectional area of the thighbone
A = π × (2 × 10-2)2 m2
= 1.26 × 10-3 m2
Using \(\frac{(F \times L)}{(A \times \Delta L)}\) the compression in each thigbone (∆L) can be computed as
∆L = \(\frac{F \times L}{Y \times A}\)
= [(1078 × 0.5)/(9.4 9 × 109 × 1.26 × 10-3)]
= 4.55 × 10-5 m or 4.55 × 10-3 cm.
This is a very small change ! The fractional decrease in the thighbone is ∆L/L = 0.000091 or 0.0091%.
Question 4.
A square slab of side 50 cm and thickness 10 cm is subject to a shearing force (on its narrow face) of 9.0 × 104 N. The lower edge is riveted to the floor. How much will the upper edge be displaced ?
Answer:
The area (A) = 50 cm × 10 cm
= 0.5 m × 0.1 m
= 0.05 m2
Therefore, the stress appIid is
= (9.4 × 104N/0.05 m2)
= 1.80 × 106 N.m2
We know that shearing strain = (∆x/L)
= Stress/G.
Therefore the displacement
∆x = (Stress × L)/G = \(\frac{\left(1.8 \times 10^6 \mathrm{Nm}^{-2} \times 0.5 \mathrm{~m}\right)}{5.6 \times 10^9 \mathrm{Nm}^{-2}}\)
= 1.6 × 10-4 m = 0.16 mm.
![]()
Question 5.
The average depth of Indian Ocean is about 3000 m. Calculate the fractional compression. ∆V/V, of water at the bottom of the ocean, given that the bulk modulus of water is 2.2 × 109 Nm-2. (Take g = 10 ms-2)
Answer:
The pressure exerted by a 3000 m column of water on the bottom layer
ρ = hρg
= 3000 m × 1000 kg m-3× 10 ms-2
= 3 × 107 Nm-2
Fractional compression ∆V/V, is
∆V/V = stress \(\frac{\left(3 \times 10^7 \mathrm{Nm}^{-2}\right)}{2.2 \times 109 \mathrm{Nm}^{-2}}\)
= 1.36 × 10-2 or 1.36%