Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Chapter 4 సమీకరణ వాదం Exercise 4(d) will help students to clear their doubts quickly.
AP Inter 2nd Year Maths 2A Solutions Chapter 4 సమీకరణ వాదం Exercise 4(d)
అభ్యాసం – 4(డి)
I.
ప్రశ్న 1.
x3 + 2x2 – 4x + 1 = 0 సమీకరణపు మూలాలకు 3 రెట్లున్న మూలాలు గల బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x3 + 2x2 – 4x + 1 = 0 అనుకొనుము.
∴ కావలసిన సమీకరణం f(\(\frac{x}{3}\)) = 0
\(\left(\frac{x}{3}\right)^3+2\left(\frac{x}{3}\right)^2-\frac{4 x}{3}+1=0\)
\(\frac{x^3}{27}+\frac{2}{9} x^2-\frac{4}{3} x+1=0\)
27 గుణించగా
కావలసిన సమీకరణం x3 + 6x2 – 36x + 27 = 0
ప్రశ్న 2.
x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0 సమీకరణపు మూలాలకు 2 రెట్లున్న మూలాలు గల బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x5 – 2x4 + 3x3 – 2x2 + 4x + 3 = 0
f(\(\frac{x}{2}\)) = 0 సమీకరణం కావలసిన లక్షణాలలో ఉంటుంది.
కావలసిన సమీకరణం f(\(\frac{x}{3}\)) = 0
⇒ \(\left(\frac{x}{2}\right)^5-2\left(\frac{x}{2}\right)^4+3\left(\frac{x}{2}\right)^3-2\left(\frac{x}{2}\right)^2+4\left(\frac{x}{2}\right)\) + 3 = 0
⇒ \(\frac{x^5}{32}-2 \cdot \frac{x^4}{16}+3 \cdot \frac{x^3}{8}-2 \cdot \frac{x^2}{4}+4 \cdot \frac{x}{2}+3=0\)
32 చే గుణించగా
కావలసిన సమీకరణం x5 – 4x4 + 12x3 – 16x2 + 64x + 96 = 0
![]()
ప్రశ్న 3.
x4 + 5x3 + 11x + 3 = 0 సమీకరణ మూలాలకు వ్యతిరేక గుర్తులు కలిగిన సంఖ్యలు మూలాలుగా గల రూపాంతర సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x4 + 5x3 + 11x + 3 = 0
-α1, -α2, -α3, -α4 లు మూలాలుగా గల సమీకరణం f(-x) = 0
⇒ (-x)4 + 5(-x)3 + 11(-x) + 3 = 0
⇒ x4 – 5x3 – 11x + 3 = 0
ప్రశ్న 4.
x7 + 3x5 + x3 – x2 + 7x + 2 = 0 సమీకరణం మూలాలకు వ్యతిరేక గుర్తులు కలిగిన సంఖ్యలు మూలాలుగా గల రూపాంతర సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x7 + 3x5 + x3 – x2 + 7x + 2 = 0
-α1, -α2, …….., -α7 లు మూలాలుగల
సమీకరణం f(-x) = 0
⇒ (-x)7 + 3(-x)5 + (-x)3 – (-x)2 + 7(-x) + 2 = 0
⇒ -x7 – 3x5 – x3 – x2 – 7x + 2 = 0
⇒ x7 + 3x5 + x3 + x2 + 7x – 2 = 0
ప్రశ్న 5.
x4 – 3x3 + 7x2 + 5x – 2 = 0 సమీకరణ మూలాల వ్యుత్కమాలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి. [Mar. ’11]
సాధన:
దత్త సమీకరణం f(x) = x4 – 3x3 + 7x2 + 5x – 2 = 0
కావలసిన సమీకరణం f(\(\frac{1}{x}\)) = 0
⇒ \(\frac{1}{x^4}-\frac{3}{x^3}+\frac{7}{x^2}+\frac{5}{x}-2=0\)
x4 చే గుణించగా
⇒ 1 – 3x + 7x2 + 5x3 – 2x4 = 0
⇒ 2x4 – 5x3 – 7x2 + 3x – 1 = 0
![]()
ప్రశ్న 6.
x5 + 11x4 + x3 + 4x2 – 13x + 6 = 0 సమీకరణం మూలాల వ్యుత్కమాలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x5 + 11x4 + x3 + 4x2 – 13x + 6 = 0
కావలసిన సమీకరణం f(\(\frac{1}{x}\)) = 0
\(\frac{1}{x^5}+\frac{11}{x^4}+\frac{1}{x^3}+\frac{4}{x^2}-\frac{13}{x}+6=0\)
x5 చే గుణించగా
⇒ 1 + 11x + x2 + 4x3 – 13x4 + 6x5 = 0
⇒ 6x5 – 13x4 + 4x3 + x2 + 11x + 1 = 0
II.
ప్రశ్న 1.
x4 + x3 + 2x2 + x + 1 = 0 సమీకరణ మూలాల వర్గాలు మూలాలుగా గల బహుపది సమీకరణాన్ని రూపొందించండి.
సాధన:
దత్త సమీకరణం f(x) = x4 + x3 + 2x2 + x + 1 = 0
కావలసిన సమీకరణం f(√x) = 0
⇒ x2 + x√x + 2x + √x + 1 = 0
⇒ √x(x + 1) = -(x2 + 2x + 1)
వర్గం చేయగా
⇒ x(x + 1)2 = (x2 + 2x + 1)2
⇒ x(x2 + 2x + 1) = x4 + 4x2 + 1 + 4x3 + 4x + 2x2
⇒ x3 + 2x2 + x = x4 + 4x3 + 6x2 + 4x + 1
⇒ x4 + 3x3 + 4x2 + 3x + 1 = 0
ప్రశ్న 2.
x3 + 3x2 – 7x + 6 = 0 సమీకరణ మూలాల వర్గాలు మూలాలుగా గల బహుపది సమీకరణాన్ని రూపొందించండి.
సాధన:
దత్త సమీకరణం f(x) = x3 + 3x2 – 7x + 6 = 0
కావలసిన సమీకరణం f(√x) = 0
⇒ x√x + 3x – 7√x + 6 = 0
⇒ √x(x – 7) = -(3x + 6)
వర్గం చేయగా
⇒ x(x – 7)2 = (3x + 6)2
⇒ x(x2 – 14x + 49) = 9x2 + 36 + 36x
⇒ x3 – 14x2 + 49x – 9x2 – 36x – 36 = 0
⇒ x3 – 23x2 + 13x – 36 = 0
![]()
ప్రశ్న 3.
x3 + 3x2 + 2 = 0 సమీకరణ మూలాల ఘనాలు మూలాలుగా గల బహుపది సమీకరణాన్ని రూపొందించండి.
సాధన:
దత్త సమీకరణం x3 + 3x2 + 2 = 0
y = x3 అయిన x = \(y^{1 / 3}\) అవుతుంది
∴ y + 3\(y^{2 / 3}\) + 2 = 0
3y\(y^{2 / 3}\) = -(y + 2)
ఘనం చేయగా
27y2 = -(y + 2)3 = -(y3 + 6y2 + 12y + 8)
∴ y3 + 6y2 + 27y2 + 12y + 8 = 0
⇒ y3 + 33y2 + 12y + 8 = 0
కావలసిన సమీకరణం x3 + 33x2 + 12x + 8 = 0
III.
ప్రశ్న 1.
-2 తో మార్పు చెందిన x4 – 5x3 + 7x2 – 17x + 11 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బీజీయ సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x4 – 5x3 + 7x2 – 17x + 11 = 0
కావలసిన సమీకరణం f(x + 2) = 0
⇒ (x + 2)4 – 5(x + 2)3 + 7(x + 2)2 – 17(x + 2) + 11 = 0
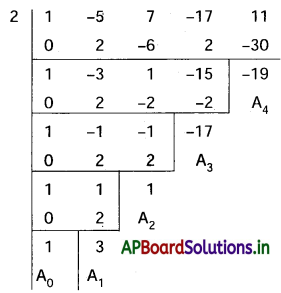
కావలసిన సమీకరణం x4 + 3x3 + x2 – 17x – 19 = 0
ప్రశ్న 2.
-3 తో మార్పు చెందిన x5 – 4x4 + 3x2 – 4x + 6 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి. [T.S. Mar. ’16]
సాధన:
దత్త సమీకరణం f(x) = x5 – 4x4 + 3x2 – 4x + 6 = 0
కావలసిన సమీకరణం f(x + 3) = 0
(x + 3)5 – 4(x + 3)3 + 3(x + 3)2 – 4(x + 3) + 6 = 0
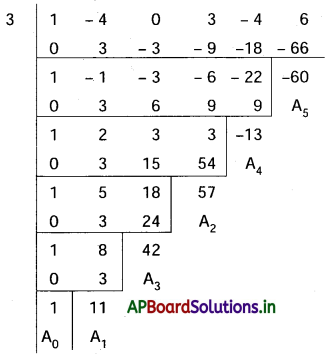
∴ కావలసిన సమీకరణం x5 + 11x4 + 42x3 + 57x2 – 13x – 60 = 0
![]()
ప్రశ్న 3.
2 తో మార్పు చెందిన x4 – x3 – 10x2 + 4x + 24 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బహుపది సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = x4 – x3 – 10x2 + 4x + 24 = 0
కావలసిన సమీకరణం f(x – 2) = 0
(x – 2)4 – (x – 2)3 – 10(x – 2)2 + 4(x – 2) + 24 = 0
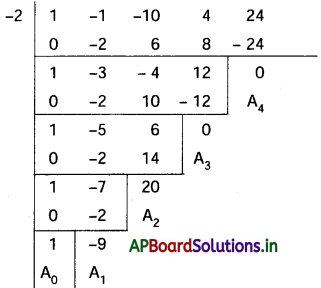
∴ కావలసిన సమీకరణం x4 – 9x3 + 20x2 = 0
ప్రశ్న 4.
4తో మార్పు చెందిన 3x5 – 5x3 + 7 = 0 సమీకరణ మూలాల విలువలు మూలాలుగా గల బహువది సమీకరణాన్ని కనుక్కోండి.
సాధన:
దత్త సమీకరణం f(x) = 3x5 – 5x3 + 7 = 0
కావలసిన సమీకరణం f(x – 4) = 0
3(x – 4)5 – 5(x – 4)3 + 7 = 0
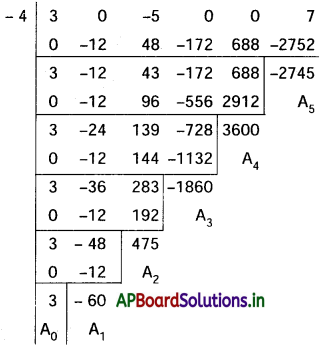
∴ కావలసిన సమీకరణం 3x5 – 60x4 + 475x3 – 1860x2 + 3600x – 2745 = 0
ప్రశ్న 5.
x యొక్క రెండో అత్యధిక ఘాత గుణకం సున్నా అయ్యే విధంగా కింది సమీకరణాలను పరివర్తన చేసి రూపాంతర సమీకరణాలను కనుక్కోండి.
(i) x3 – 6x2 + 10x – 3 = 0
సాధన:
x యొక్క రెండో అత్యధిక ఘాత గుణకం లుప్తం అయ్యే విధంగా సమీకరణ మూలాలను \(\frac{-a_1}{n \cdot a_0}=\frac{-(-6)}{(3)(1)}\) = 2 తో మూలాల విలువలను పరివర్తనము చేయాలి.
అంటే f(x + 2) = 0 ను కనుక్కోవాలి.
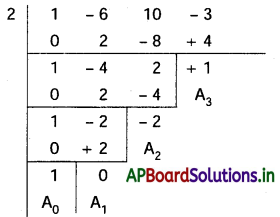
∴ కావలసిన సమీకరణము x3 – 2x + 1 = 0
(ii) x4 + 4x3 + 2x2 – 4x – 2 = 0
సాధన:
దత్త సమీకరణం x4 + 4x3 + 2x2 – 4x – 2 = 0
మూలాలను h = \(-\frac{a_1}{n a_0}=\frac{-4}{4}\) = -1 తో మార్పు చెందించాలి.
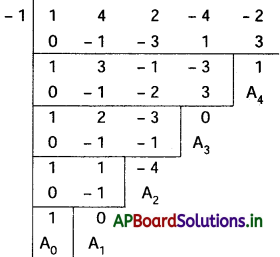
∴ కావలసిన సమీకరణం x4 – 4x2 + 1 = 0
(iii) x3 – 6x2 + 4x – 7 = 0
సాధన:
దత్త సమీకరణం x3 – 6x2 + 4x – 7 = 0
మూలాలను h = \(-\frac{a_1}{n a_0}=\frac{6}{3}\) = 2 తో మార్పు చెందించాలి.
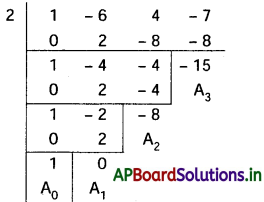
∴ కావలసిన సమీకరణం x3 – 8x – 15 = 0
(iv) x3 + 6x2 + 4x + 4 = 0
సాధన:
దత్త సమీకరణం x3 + 6x2 + 4x + 4 = 0
రెండవ పదాన్ని లోపింపచేయటానికి మూలాలను h = \(-\frac{a_1}{n a_0}=-\frac{6}{3}\) = -2 కు మార్పు చెందించాలి.
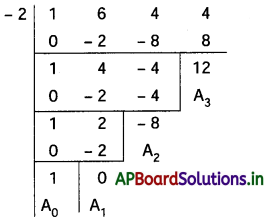
∴ కావలసిన సమీకరణం x3 – 8x + 12 = 0
![]()
ప్రశ్న 6.
x యొక్క మూడో అత్యధిక ఘాత గుణకం సున్నా అయ్యే విధంగా కింది సమీకరణాలను పరివర్తన చేయండి.
(i) x4 + 2x3 – 12x2 + 2x – 1 = 0
సాధన:
దత్త సమీకరణం
f(x) = x4 + 2x3 – 12x2 + 2x – 1 = 0
x యొక్క మూడో అత్యధిక ఘాత గుణకం సున్నా కావాలి.
అంటే, దత్త సమీకరణ, మూలాలను h కు మార్పు చెందించాలి.
ఇచ్చట h అనేది \(f^{(4-3+1)}(h)\) = 0 ⇒ \(f^{(2)} \text { (h) }\) = 0 నుండి వస్తుంది.
f'(x) = 4x3 + 6x2 – 24x + 2
f”(x) = 12x2 + 12x – 24
f”(h) = 0
⇒ 12h2 + 12h – 24 = 0
⇒ h2 + h – 2 = 0
⇒(h + 2) (h – 1) = 0
⇒ h = -2 (లేదా) 1
సందర్భము (i):
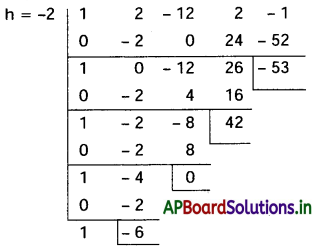
∴ కావలసిన సమీకరణం x4 – 6x3 + 42x – 53 = 0
సందర్భము (ii):
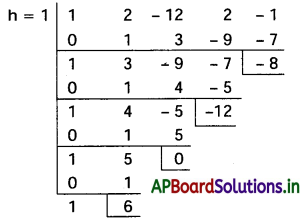
కావలసిన సమీకరణము x4 + 6x3 – 12x – 8 = 0
∴ కావలసిన సమీకరణాలు x4 – 6x3 + 42x – 53 = 0 (లేదా) x4 + 6x3 – 12x – 8 = 0
(ii) x3 + 2x2 + x + 1 = 0
సాధన:
f(x) = x3 + 2x2 + x + 1 అనుకోండి.
x యొక్క మూడో అత్యధిక గుణకం సున్నా కావాలి అంటే, దత్త సమీకరణ మూలాలను ‘h’ తో మార్పు చెందించాలి.
ఇచ్చట h అనేది f'(h) = 0 నుండి వస్తుంది.
f'(x) = 3x2 + 4x + 1
f'(h) = 0
⇒ 3h2 + 4h + 1 = 0
⇒ (3h + 1) (h + 1) = 0
⇒ h = -1, \(-\frac{1}{3}\)
సందర్భము (i):
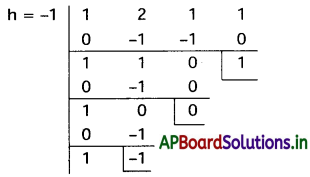
∴ కావలసిన సమీకరణం x3 – x2 + 1 = 0
సందర్భము (ii):
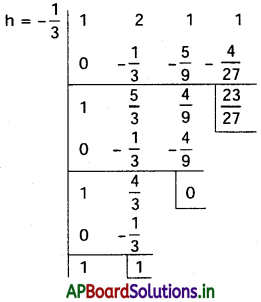
∴ కావలసిన సమీకరణం x3 + x2 + \(\frac{23}{27}\) = 0
⇒ 27x3 + 27x2 + 23 = 0
∴ కావలసిన సమీకరణాలు x3 – x2 + 1 = 0 (లేదా) 27x3 + 27x2 + 23 = 0
![]()
ప్రశ్న 7.
కింది సమీకరణాలను సాధించండి.
(i) x4 – 10x3 + 26x2 – 10x + 1 = 0
సాధన:
దత్త సమీకరణం ఒకటో కోవకు చెందిన సరిఘాత వ్యుత్కమ సమీకరణం
x2 చే భాగించగా x2 – 10x + 26 – \(\frac{10}{x}+\frac{1}{x^2}\) = 0
\([latex]\frac{10}{x}+\frac{1}{x^2}\)[/latex] …….(1)
a = x + \(\frac{1}{x}\) అనుకుంటే
\(x^2+\frac{1}{x^2}=\left(x-\frac{1}{x}\right)^2-2\) = a2 – 2
(1) లో వ్రాయగా a2 – 2 – 10a + 26 = 0
⇒ a2 – 10a + 24 = 0
⇒ (a – 4) (a – 6) = 0
⇒ a = 4 (లేదా) 6
సందర్భము (i): a = 4
x + \(\frac{1}{x}\) = 4
⇒ x2 + 1 = 4x
⇒ x2 – 4x + 1 = 0
⇒ x = \(\frac{4 \pm \sqrt{16-4}}{2}=\frac{4 \pm 2 \sqrt{3}}{2}\)
⇒ x = 2 ± √3
సందర్భము (ii): a = 6 అయిన
x + \(\frac{1}{x}\) = 6
⇒ x2 + 1 = 6x
⇒ x2 – 6x + 1 = 0
⇒ x = \(\frac{6 \pm \sqrt{36-4}}{2}=\frac{6 \pm 4 \sqrt{2}}{2}\)
⇒ x = 3 ± 2√2
∴ దత్త సమీకరణానికి మూలాలు 3 ± 2√2, 2 ± √3
(ii) 2x5 + x4 – 12x3 – 12x2 + x + 2 = 0 [A.P. Mar ’16, Mar. ’08, ’07]
సాధన:
f(x) = 2x5 + x4 – 12x3 – 12x2 + x + 2 = 0
ఒకటవ కోవకు చెందిన బేసి తరగతి వ్యుత్కమ సమీకరణం
∴ -1 మూలం
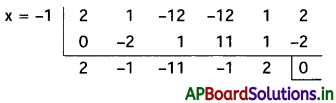
f(x) ను (x + 1) చే భాగించగా
2x4 – x3 – 11x2 – x + 2 = 0
x2 చే భాగించగా
2x2 – x – 11 – \(\frac{1}{x}+\frac{2}{x^2}\) = 0
\(2\left(x^2+\frac{1}{x^2}\right)-\left(x+\frac{1}{x}\right)-11=0\) ………(1)
a = x + \(\frac{1}{x}\) అయిన x2 + \(\frac{1}{x^2}\) = a2 – 2
(1) లో వ్రాయగా
2(a2 – 2) – a – 11 = 0
⇒ 2a2 – 4 – a – 11 = 0
⇒ 2a2 – a – 15 = 0
⇒ (a – 3) (2a + 5) = 0
⇒ a = 3 లేదా \(\frac{-5}{2}\)
సందర్భము (i): a = 3 అయిన
x + \(\frac{1}{x}\) = 3
⇒ x2 + 1 = 3x
⇒ x2 – 3x + 1 = 0
⇒ x = \(\frac{3 \pm \sqrt{9-4}}{2}=\frac{3 \pm \sqrt{5}}{2}\)
సందర్భము (ii): a = \(\frac{-5}{2}\) అయిన
\(x+\frac{1}{x}=-\frac{5}{2}\)
⇒ \(\frac{x^2+1}{x}=-\frac{5}{2}\)
⇒ 2x2 + 2 = -5x
⇒ 2x2 + 5x + 2 = 0
⇒ (2x + 1) (x + 2) = 0
⇒ x = \(\frac{-1}{2}\), -2
∴ దత్త సమీకరణానికి మూలాలు -1, \(\frac{-1}{2}\), -2, \(\frac{3 \pm \sqrt{5}}{2}\)