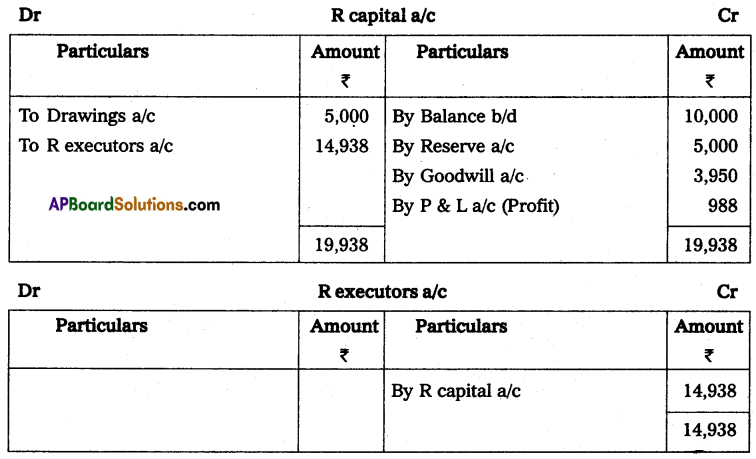
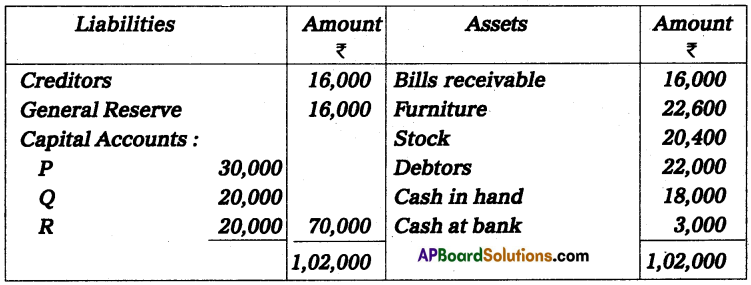
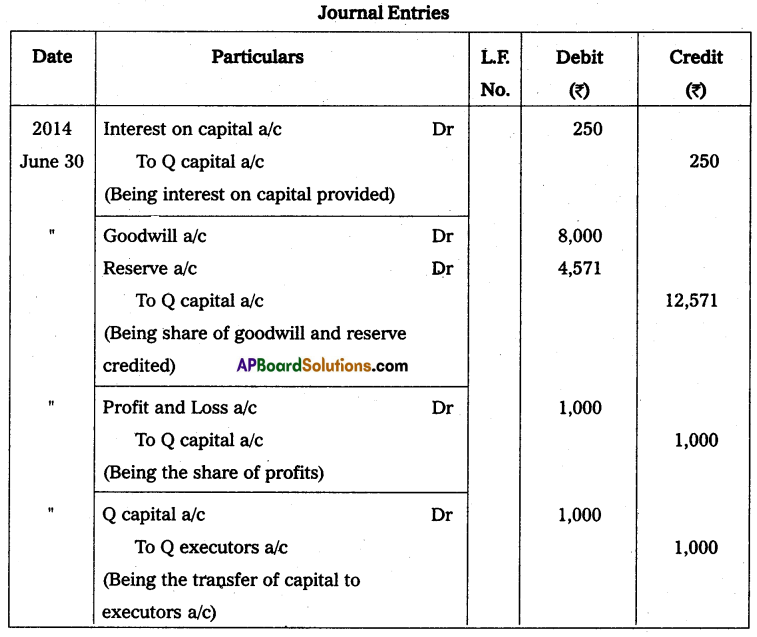
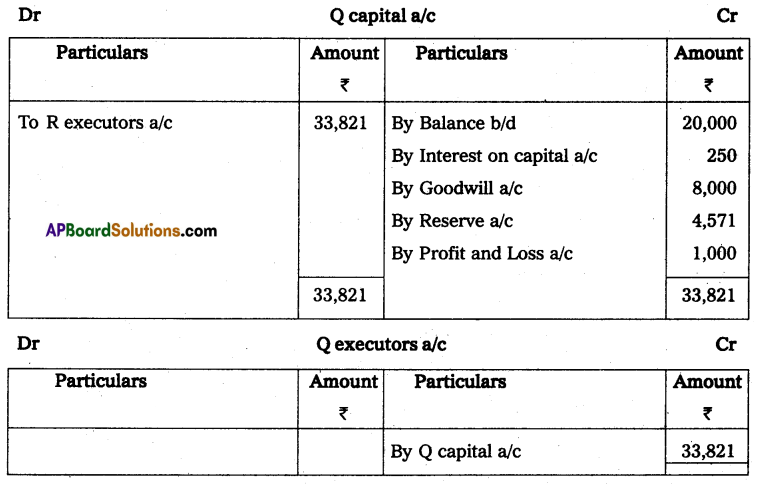
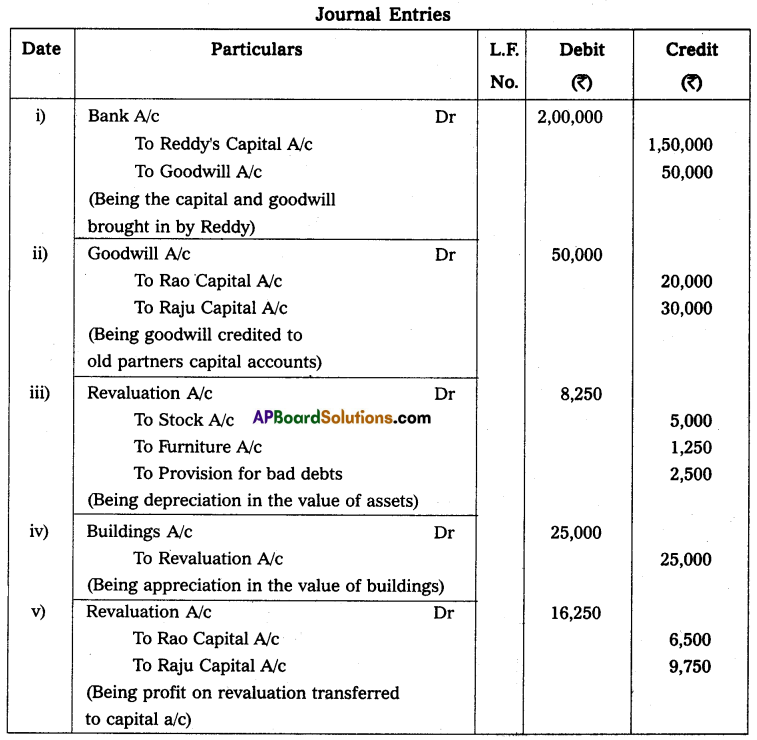
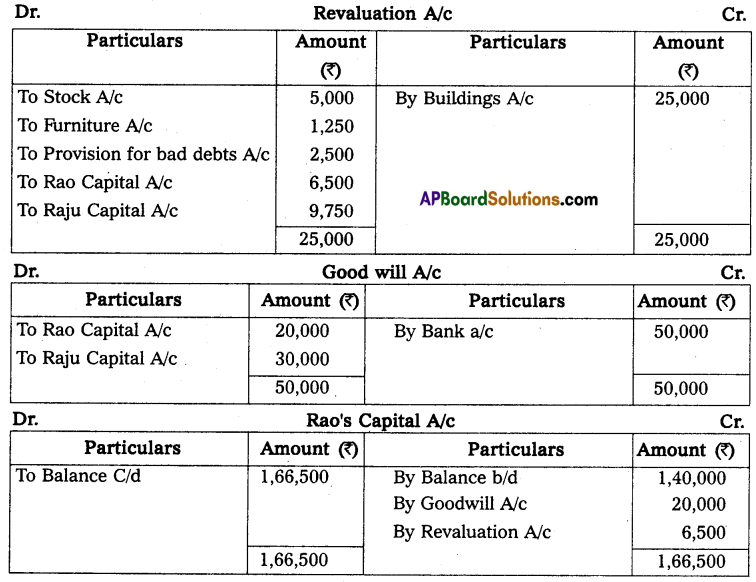
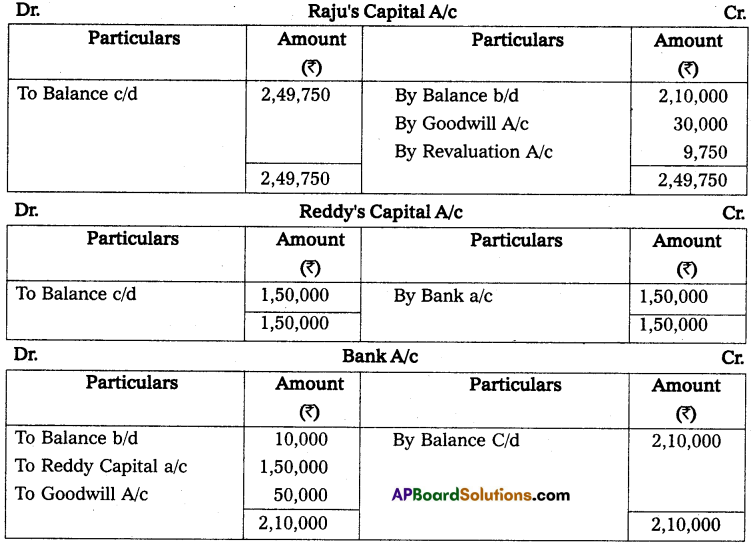
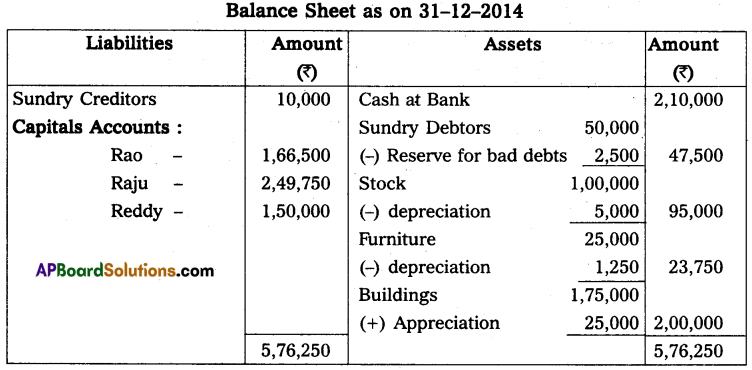
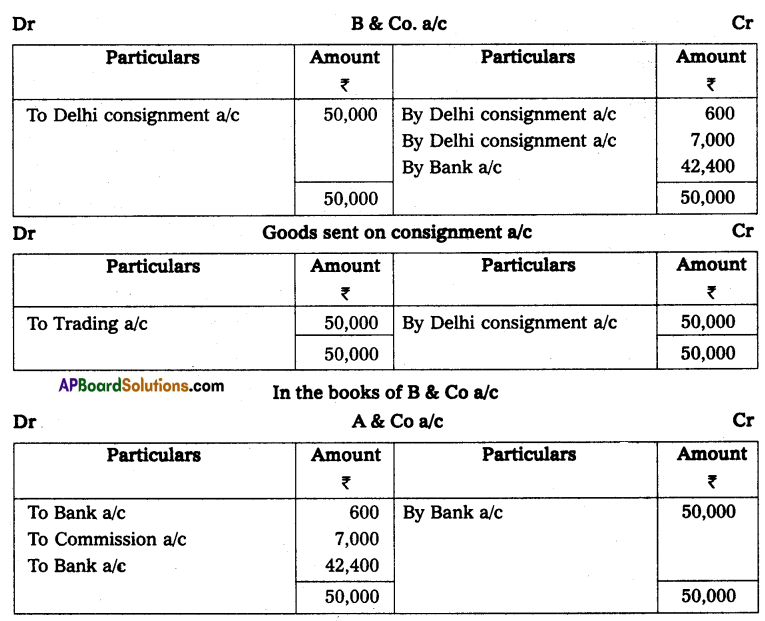
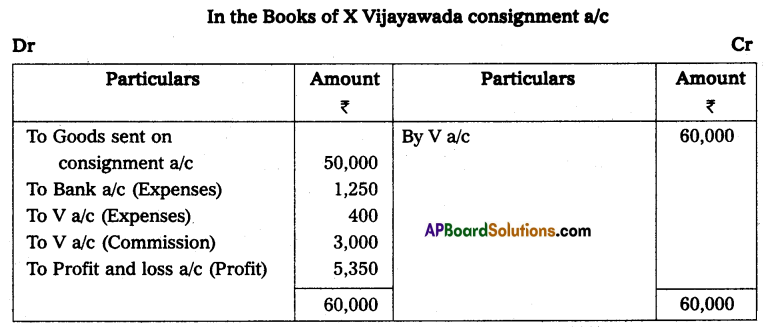
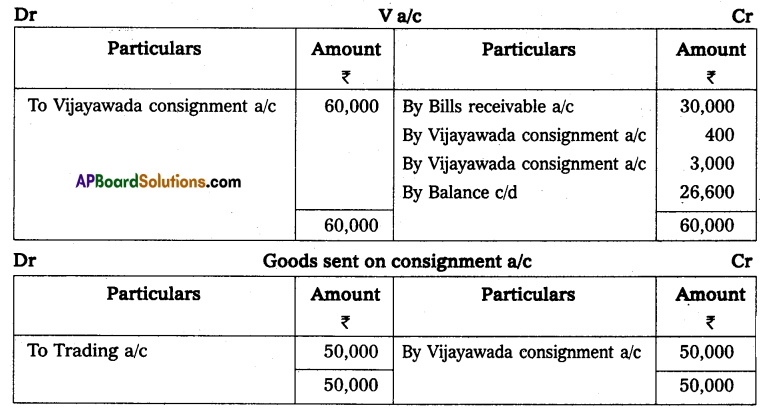
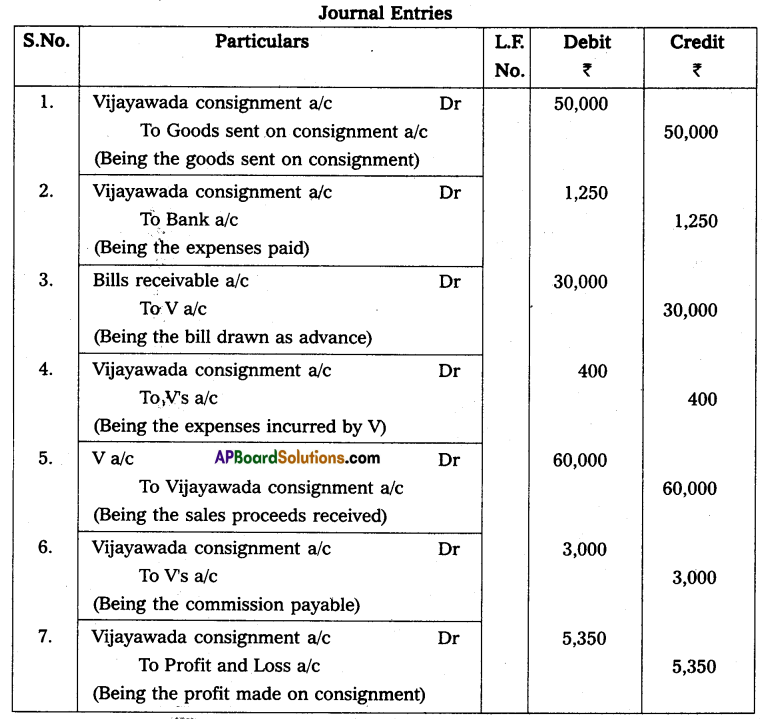
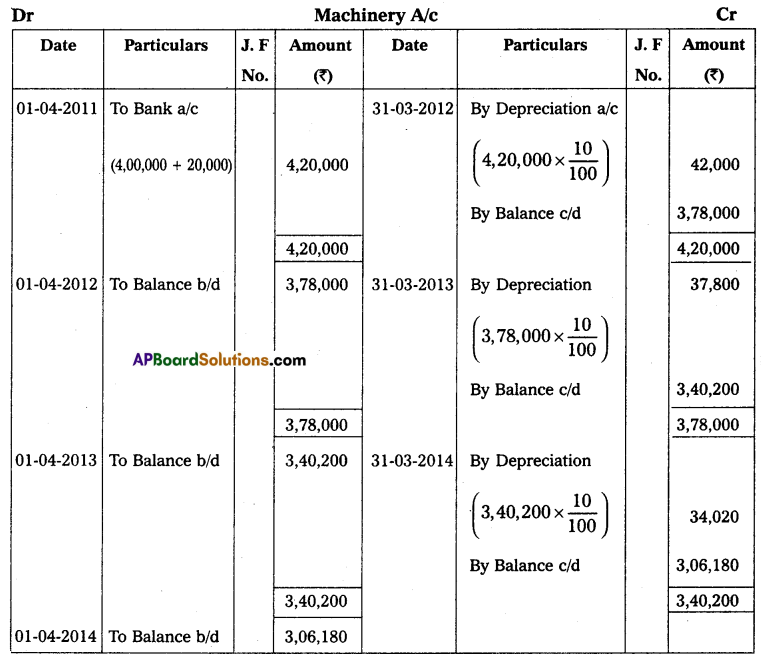
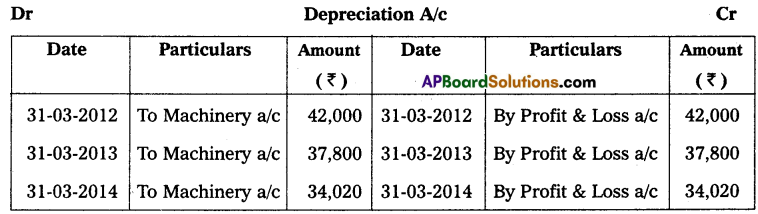
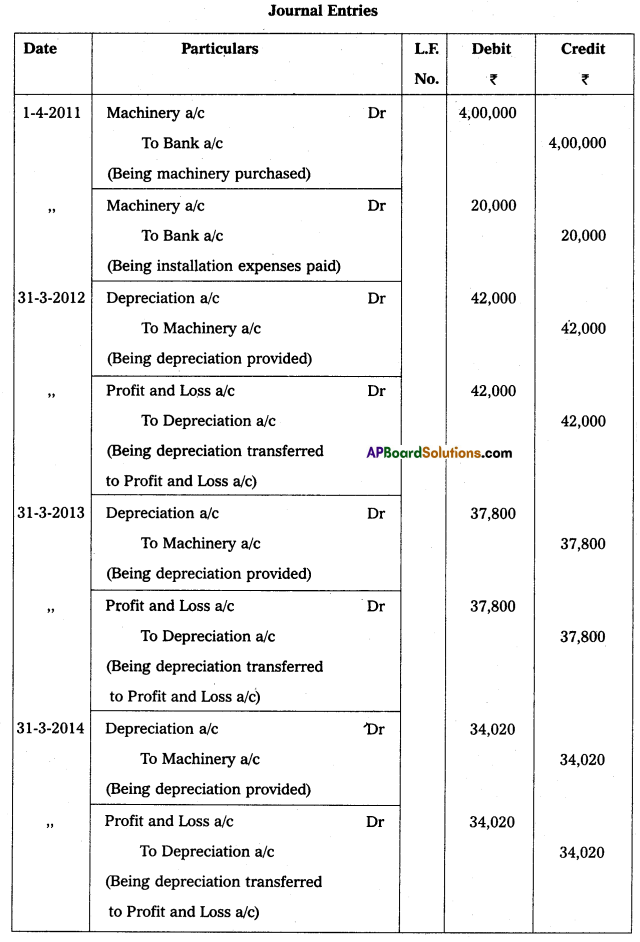
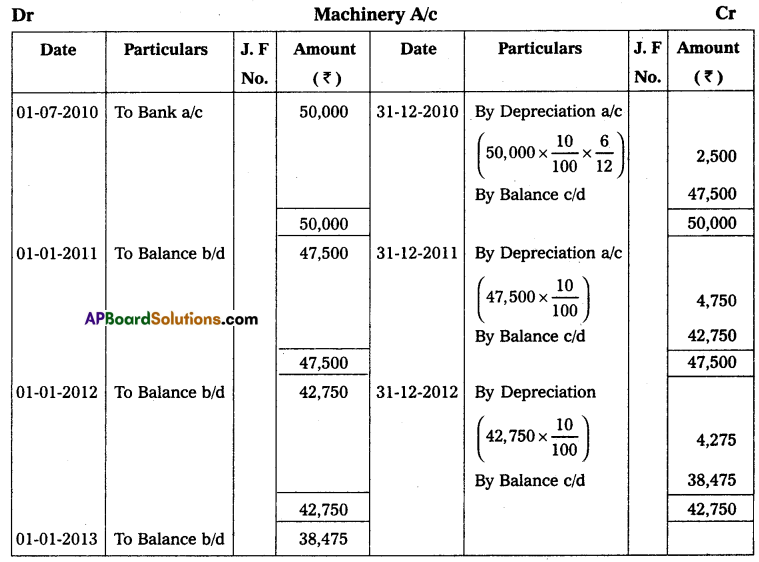
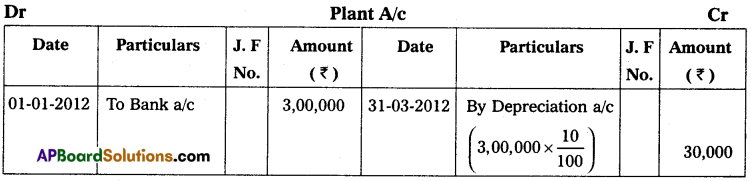
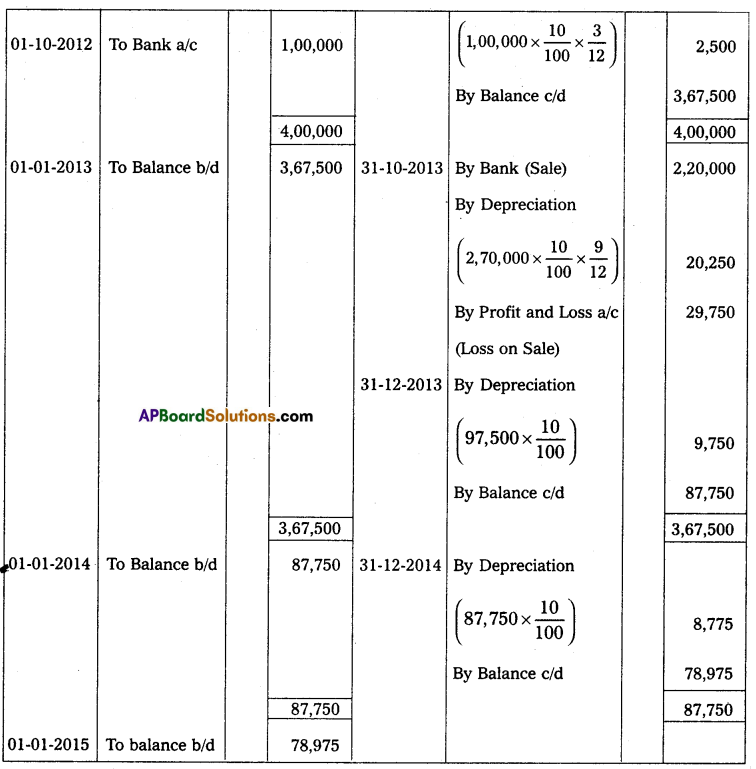
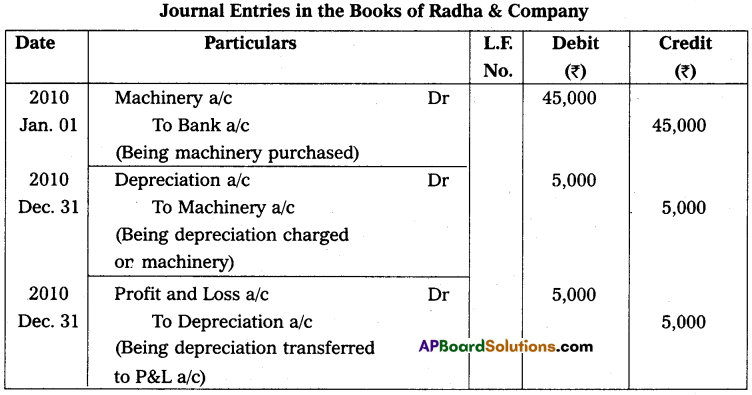
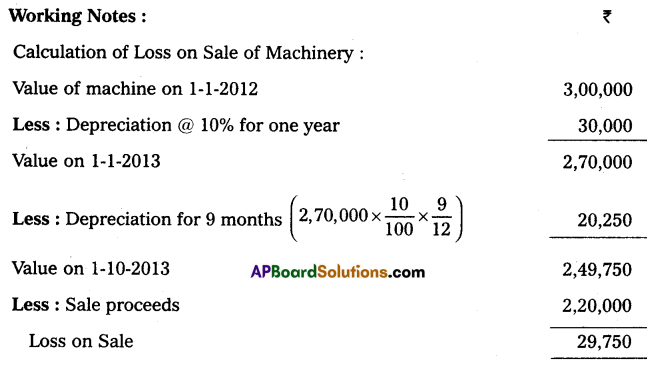Andhra Pradesh BIEAP AP Inter 2nd Year Accountancy Study Material 10th Lesson Accounts from Incomplete Records Textbook Questions and Answers.
AP Inter 2nd Year Accountancy Study Material 10th Lesson Accounts from Incomplete Records
Short Answer Questions
Question 1.
What is meant by accounts from Incomplete records?
Answer:
Accounting records that are not strictly kept according to the double entry system are known as accounts from incomplete records. It simply means the principles of the double entry system are not being followed for all transactions.
Question 2.
Define accounts from Incomplete records.
Answer:
Definition: According to R.N. Carter, a single entry cannot be termed as a system, as it is hot based on any scientific system like a double entry system, for this purpose, a single entry is nowadays known as the preparation of accounts from incomplete records.
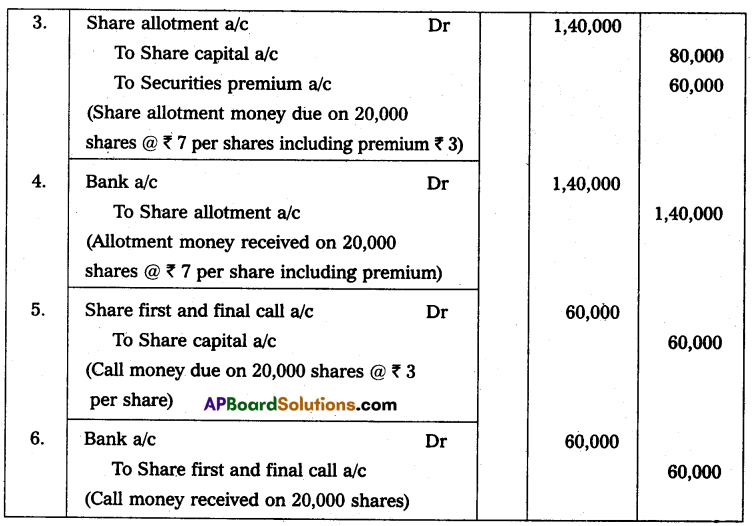
![]()
Question 3.
What are the uses of Incomplete records?
Answer:
Uses of accounts from incomplete records:
- Single entry is a simple method of recording transactions.
- It is less expensive when compared to the double-entry system of bookkeeping.
- It is mainly suitable for small business concerns with a limited number of transactions.
- It is very easy to follow, a person without any adequate knowledge of the principles of accounting can understand it.
- Ascertainment of profit or loss is very easy.
Question 4.
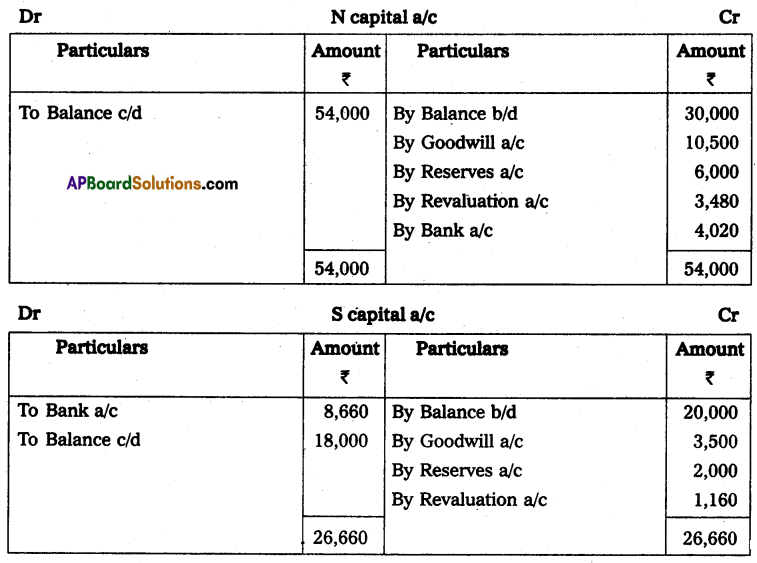
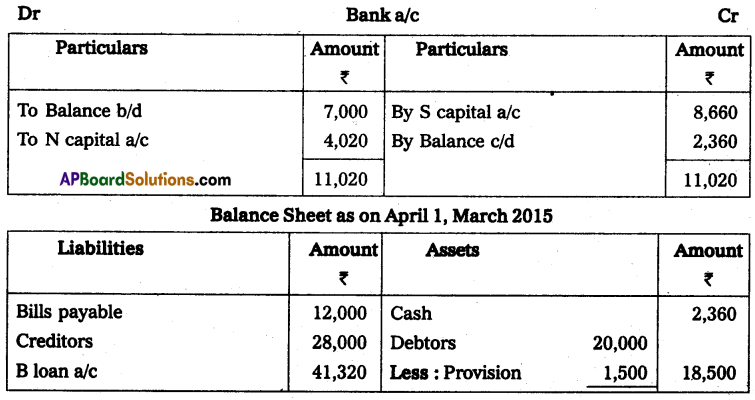
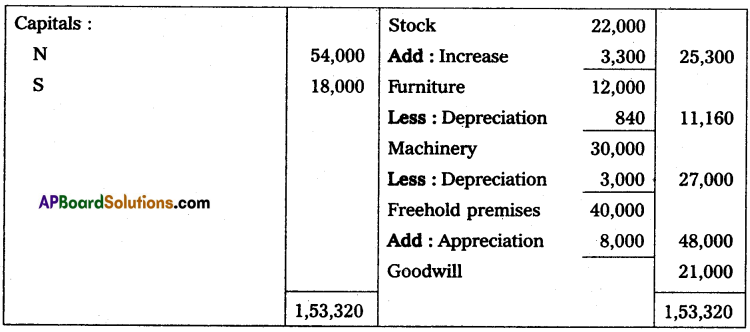
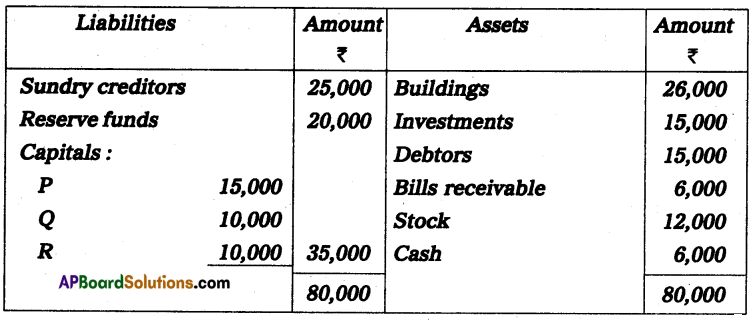
Write briefly the salient features of Incomplete records.
Answer:
Features of accounts from incomplete records:
- It is not a systematic method of recording transactions.
- It is very common to keep only personal accounts.
- It avoids real and nominal accounts.
- It is very common to keep a cashbook to record cash receipts and cash payments.
- This system lacks uniformity as it differs from firm to firm.
- It is most suitable and used by sole traders and partnership concerns.
Question 5.
Give two main differences between a statement of affairs and a balance sheet.
Answer:
The following are the differences between a Statement of Affairs and a Balance Sheet.
| Basis | Statement of Affairs | Balance Sheet |
| 1. Purpose | It shows the financial position as well as finding out capital in ascertaining profit/loss. | It shows the financial position on a particular date. |
| 2. Source | It is prepared from ledger balances and partly from other particulars and estimates etc. | It is prepared from balances only. |
| 3. Accounting Method | It is prepared when accounts are prepared under a single entry. | It is prepared when accounts are maintained double-entry system. |
| 4. Reliability | It is not regarded as reliable as it is based partly on accounts and partly on other information. | It is reliable as it is based on actual figures. |
| 5. Capital Account | Capital is the excess of assets over liabilities. | Capital is taken from the ledger. |
| 6. Trail Balance | Trail balance is not prepared. | Trail balance is prepared. |
| 7. Omission | In this statement, omission assets and liabilities cannot be tracked. | Any omission of an asset or liability can be easily traced as the total will not agree. |
Question 6.
How to ascertain profit under Incomplete records?
Answer:
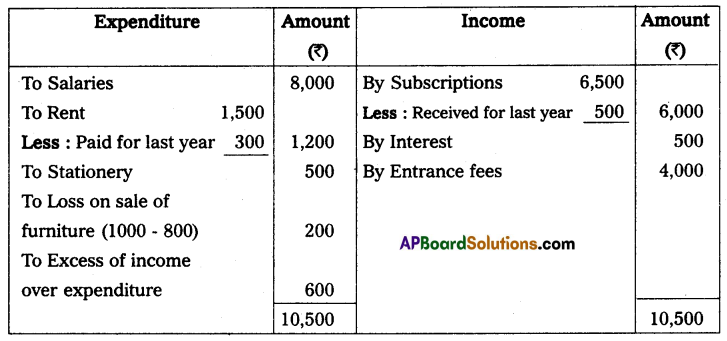
Under a single-entry system, net profit is ascertained by calculating capital at the end and capital at the beginning by preparing two statements of affairs. Then the capital at the end will be added by drawings during the year and subtracting additional capital brought in. The difference between the adjusted capital and capital at the beginning is either a net profit or a net loss.
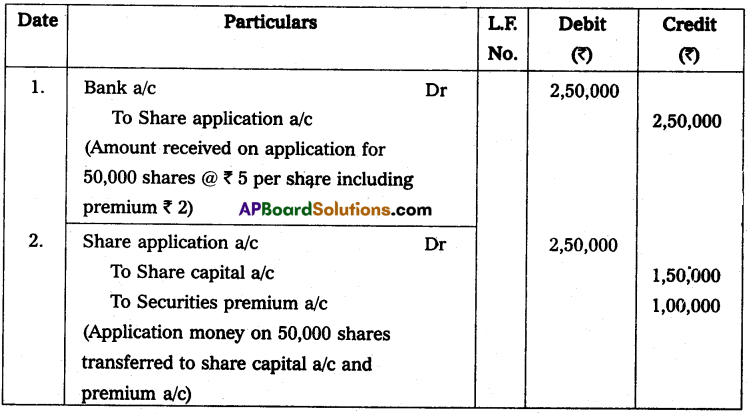
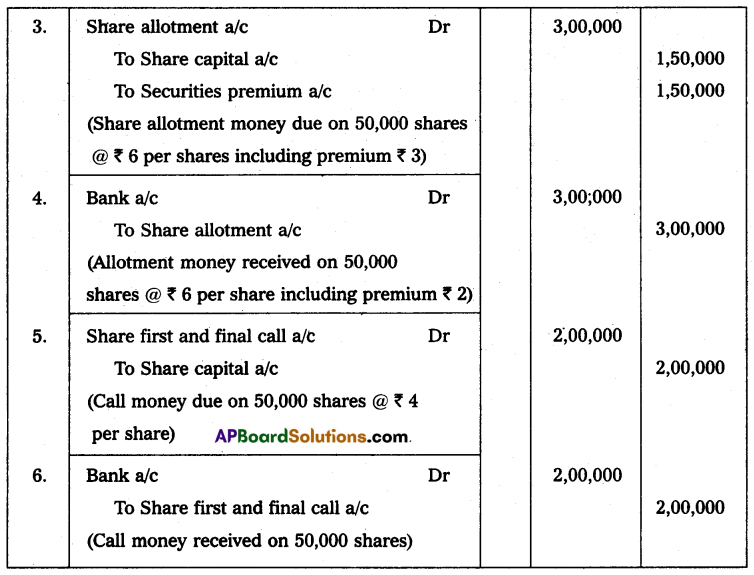
![]()
Question 7.
Write in brief the limitations of Incomplete records of bookkeeping.
Answer:
The following are the limitations of accounts from incomplete records.
- It is not a scientific method of accounting because it does not record the two-fold aspect of each transaction.
- No trail balance can be prepared as it does not record the duel aspect of each transaction, so, the arithmetical accuracy of the books cannot be checked.
- In the absence of nominal accounts, trading and profit and loss account cannot be prepared.
- In the absence of real accounts, it is not possible to know the exact financial position of the business.
- An internal check is not possible, so the possibility of fraud or misappropriation is greater in the case of a single entry.
- Accounts prepared under a single entry do not inspire confidence in outsiders.
- It is difficult to ascertain the value of a business, specifically goodwill if the owner wishes to sell his business.
Question 8.
Write any differences between the double-entry system and the single-entry system.
Answer:
The following are the differences between a double-entry system and a single-entry system.
| Basis | Double Entry System | Single Entry System |
| 1. Type | It is a perfect and complete system of bookkeeping. | It is an incomplete system and a crude method. |
| 2. Nature | This system is scientific and follows certain accounting principles. | This system is unscientific and does not follow accounting principles. |
| 3. Two Aspects | Both the debit and credit aspects of each transaction are recorded. | Both aspects are not recorded. |
| 4. Records | It provides complete and detailed records of the business. | It does not provide complete and detailed records of the business. |
| 5. Accounts | In this, all types of accounts, namely personal, real and nominal accounts are maintained. | In this, personal accounts are maintained except the cashbook. Real and nominal accounts are ignored. |
| 6. Trail Balance | The arithmetical accuracy of accounts can be checked by preparing a trial balance. | Trail balance cannot be prepared to check the arithmetical accuracy. |
| 7. Ascertainment of Profit | Profit can be ascertained by preparing trading and profit and loss a/c. | The difference between capital at the beginning and end is treated as profit. |
| 8. Cost | Relatively it is more expensive. | Relatively it is less expensive. |
| 9. Suitability | It is suitable for all types of business organisations. | It is suitable for only small business concerns. |
| 10. Errors | Errors can be easily detected and rectified. | Errors cannot be detected and rectified. |
| 11. True Financial Position | The balance sheet can be prepared to know the true and fair financial position. | The balance sheet cannot be prepared and only a statement of affairs can be prepared to know the financial position in a rough manner. |
Textual Exercises
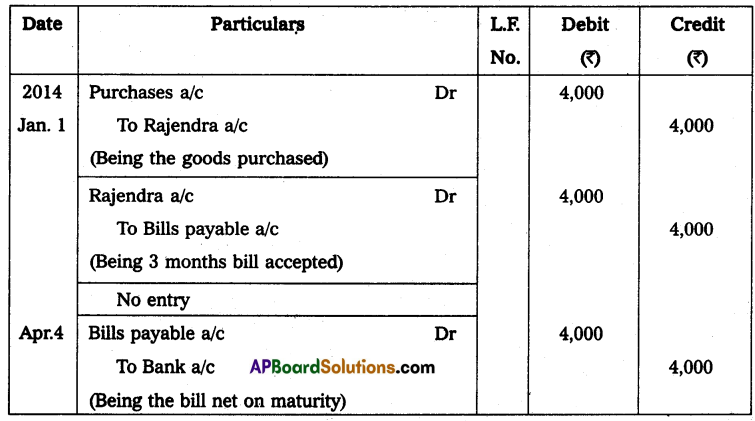
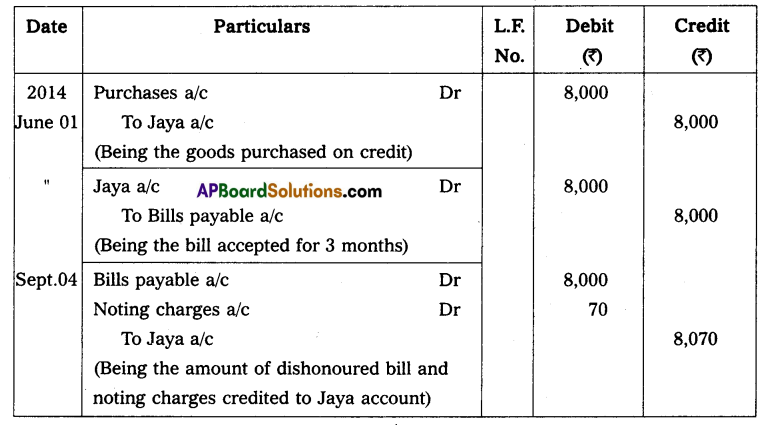
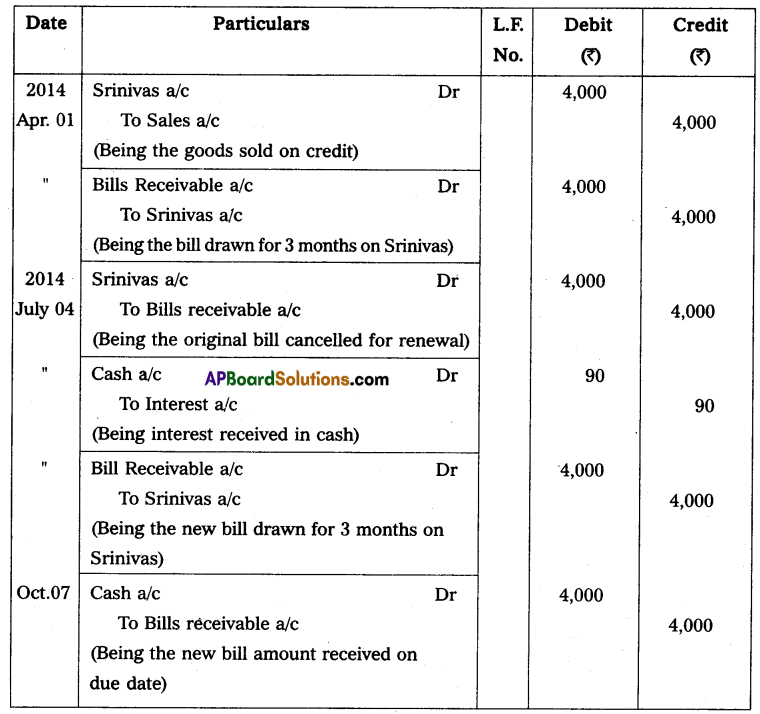
Question 1.
From the following find the profit earned by a trader.
Capital at the beginning of the year – ₹ 7,500
Capital at the end of the year – ₹ 10,000
Solution:
Statement of Profit or Loss

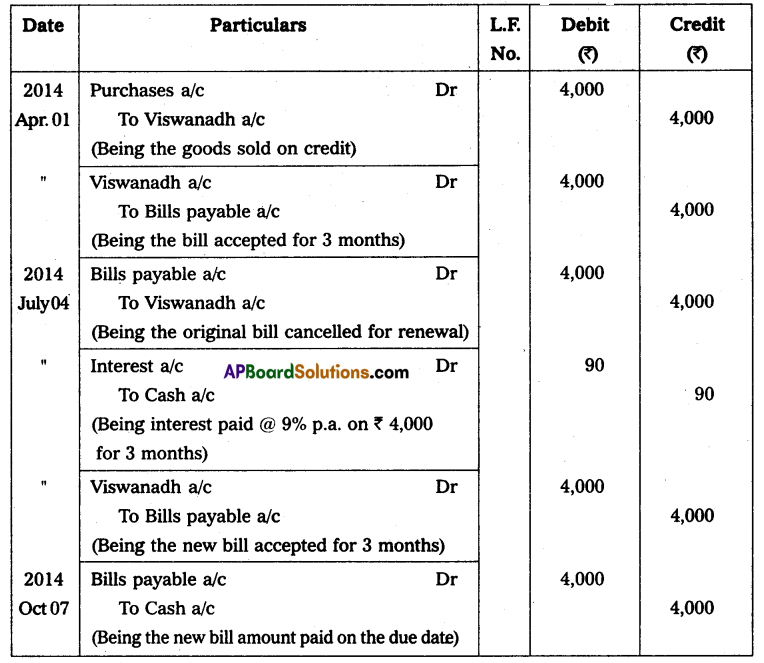
Question 2.
Calculate the profit or loss of a concern
Capital at the beginning of the year – ₹ 15,000
Capital at the end of the year – ₹ 14,000
Solution:
Statement of Profit or Loss

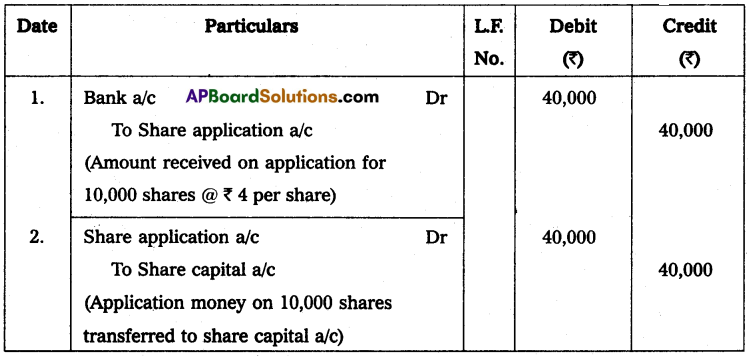
![]()
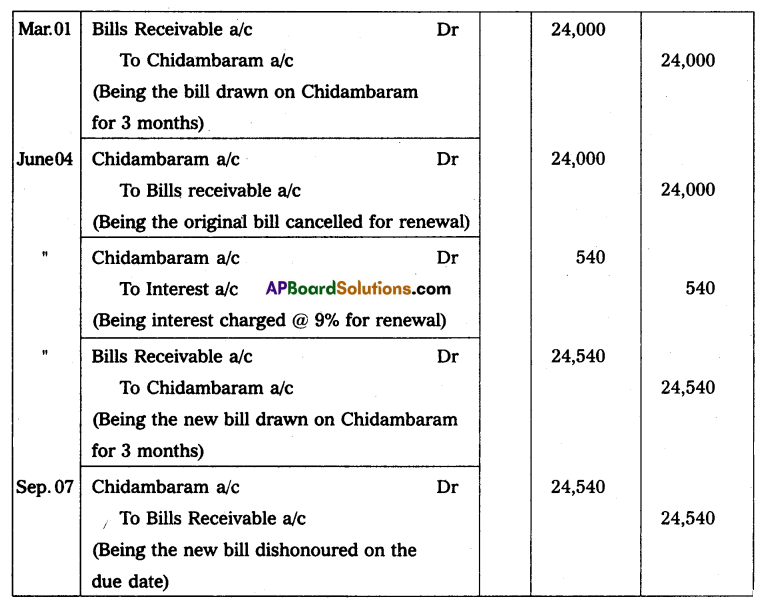
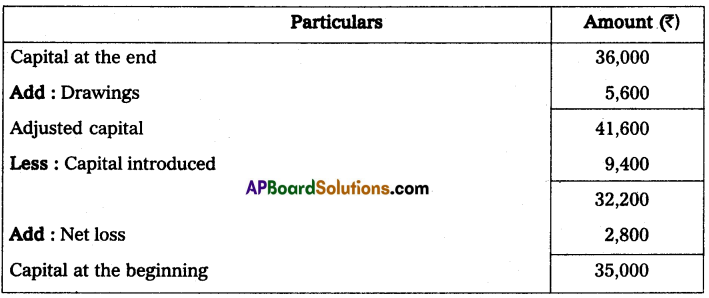
Question 3.
Calculate the missing figure
Capital at the beginning – ?
Capital at the end – ₹ 36,000
Capital introduced – ₹ 9,400
Drawings – ₹ 5,600
Loss – ₹ 2,800
Solution:
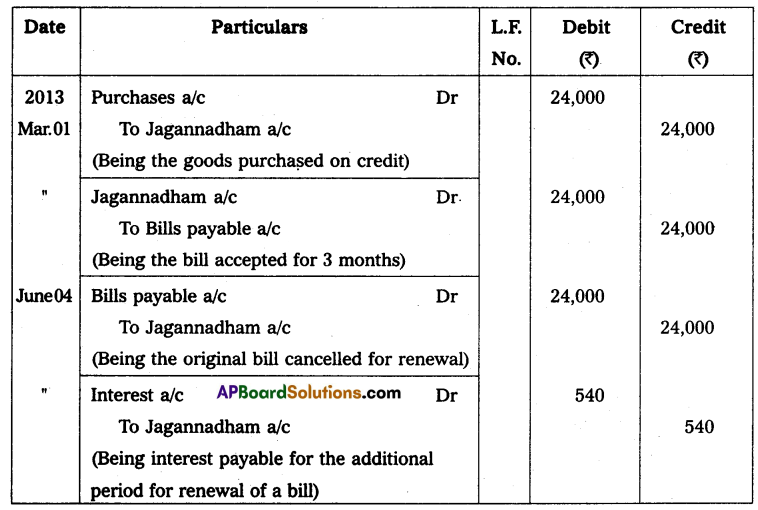
Question 4.
Find out the profit from the following data:
Capital at the beginning of the year – ₹ 40,000
Capital at the end of the year – ₹ 45,000
Drawings during the year – ₹ 5,000
Capital introduced during the year – ₹ 2,500
Solution:
Statement showing Profit or Loss

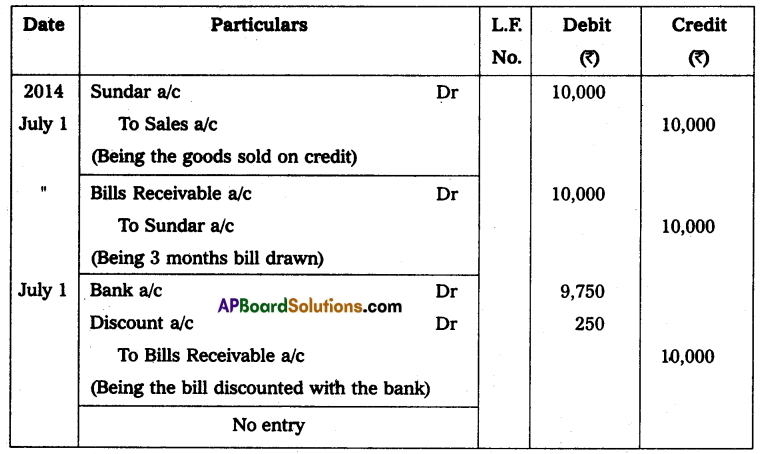
Question 5.
Find out the profit from the following data:
Capital at the beginning of the year – ₹ 60,000
Capital at the end of the year – ₹ 67,500
Drawings during the year – ₹ 7,500
Additional capital introduced during the year – ₹ 3,750
Solution:
Statement showing Profit or Loss

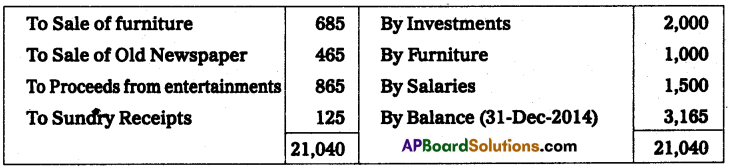
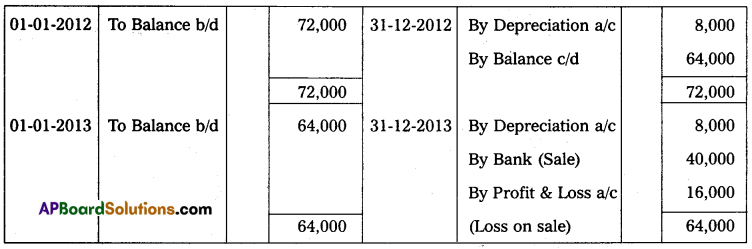
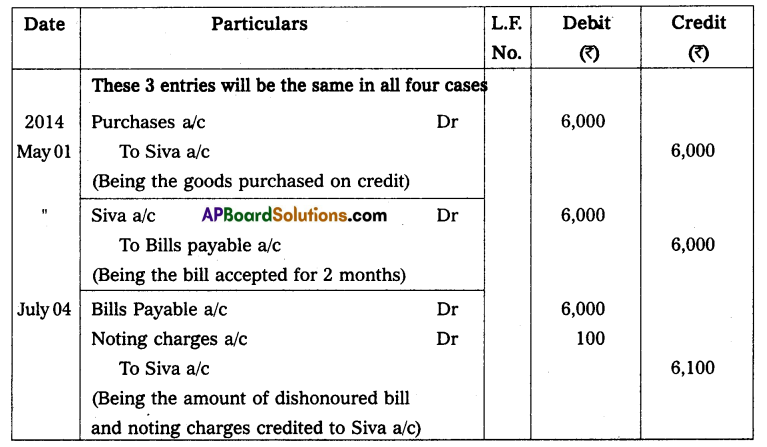
Question 6.
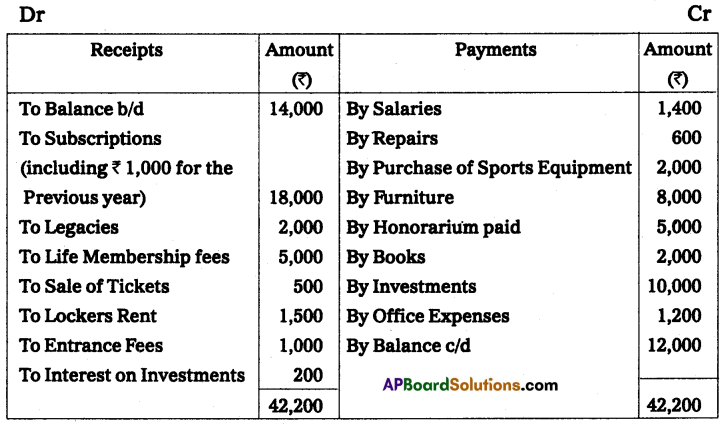
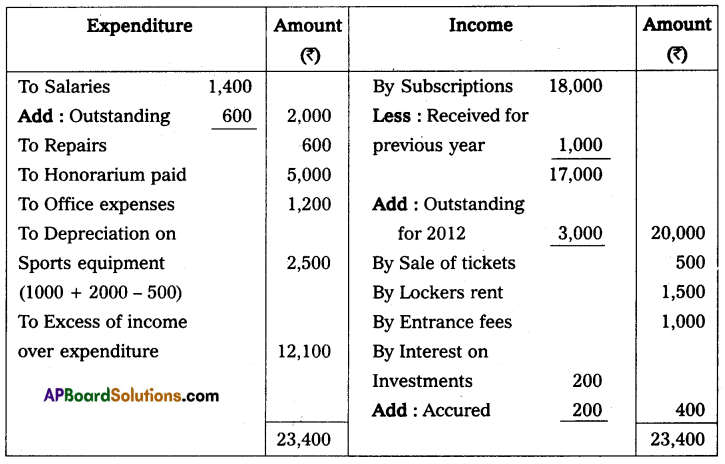
Ascertain profit earned by a trader who keeps these books under a single entry system.
(i) Excess of assets over liabilities as of 31-12-2014 – ₹ 26,150
(ii) Additional capital introduced during the year – ₹ 7,500
(iii) Drawings during the year – ₹ 4,800
(iv) Capital as on 01-01-2014 – ₹ 15,000
Solution:
Statement showing Profit or Loss

![]()
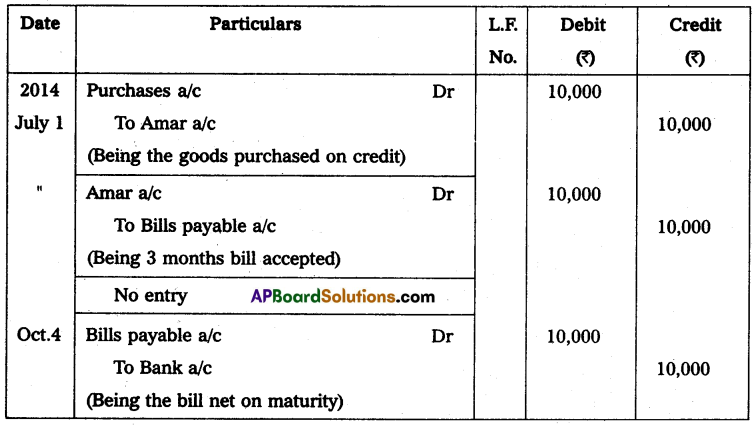
Question 7.
Following the information given below prepare this statement of profit or loss.
(i) Capital at the end of the year – ₹ 2,00,000
(ii) Capital at the beginning of the year – ₹ 1,20,000
(iii) Drawings made during the period – ₹ 30,000
(iv) Additional capital introduced – ₹ 50,000
Solution:
Statement showing Profit or Loss

Question 8.
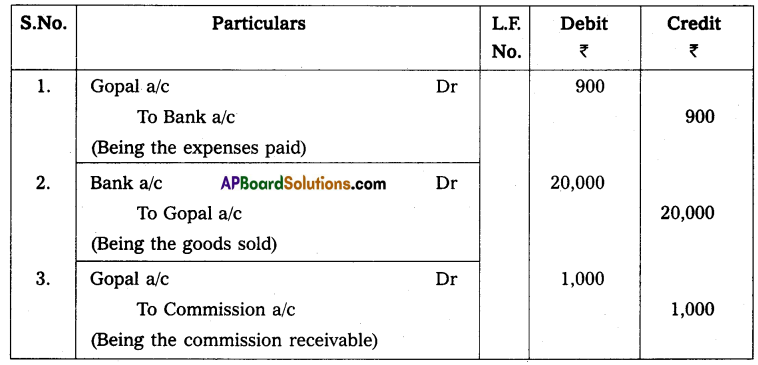
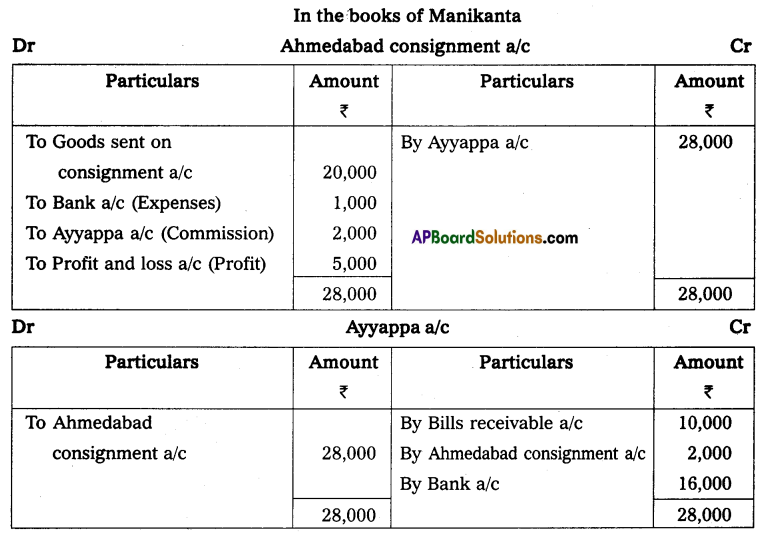
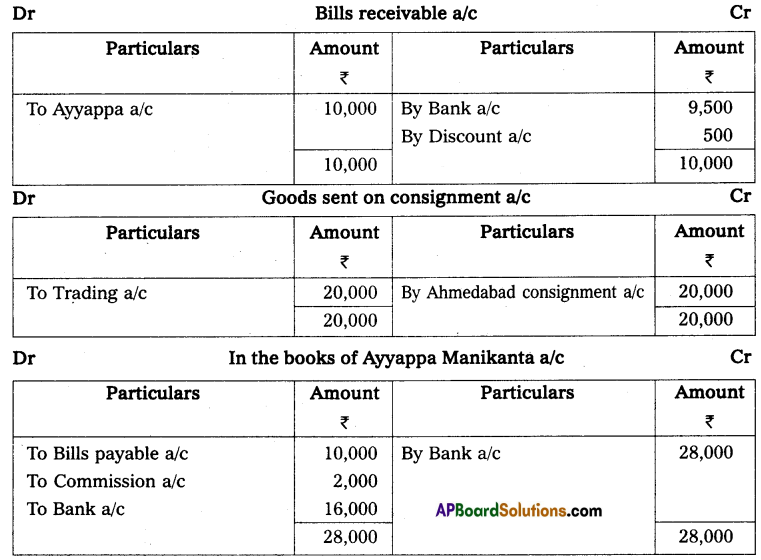
Mr. Gopal maintains his books on single entry method he was given the following information:
Capital on 01-04-2013 – ₹ 38,000
Capital on 31-3-2014 – ₹ 44,000
Drawings during the year – ₹ 14,000
Additional capital introduced during the year – ₹ 8,000
You are required to calculate profit or loss.
Solution:
Statement showing Profit or Loss

Question 9.
Mr. Jeevan maintains his books in the single entry system he gives the following information.
Capital on 01-04-2013 – ₹ 48,000
Drawings dining the year – ₹ 15,000
Capital as on 31-03-2014 – ₹ 54,000
Additional capital introduced during the year – ₹ 9,000
You are requested to prepare a statement of profit or loss for the 31-03-2014
Solution:
Statement showing Profit or Loss

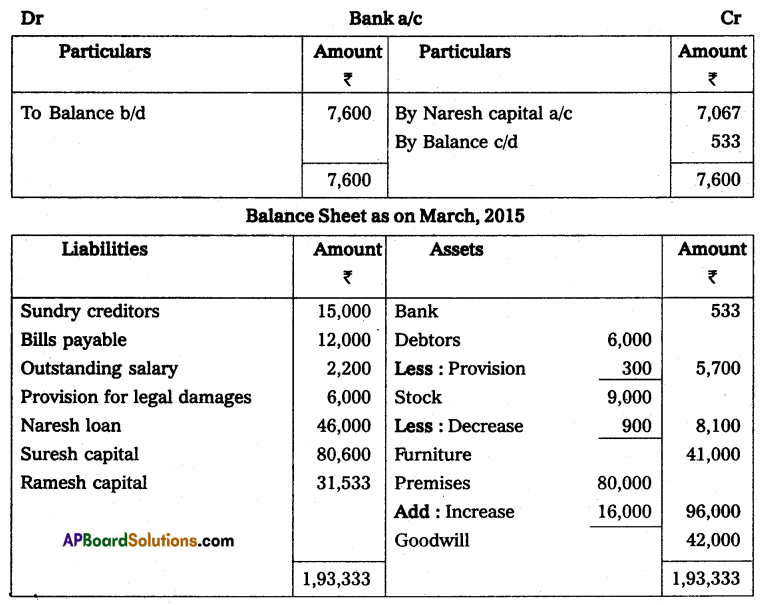
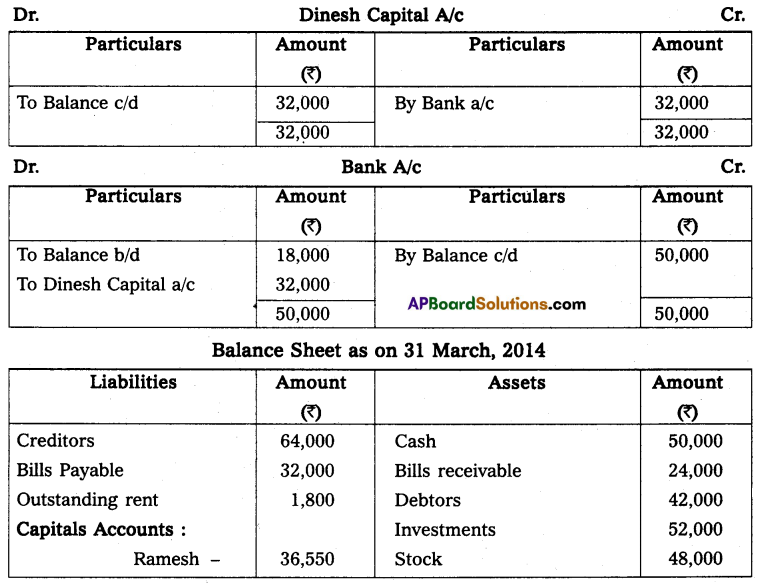
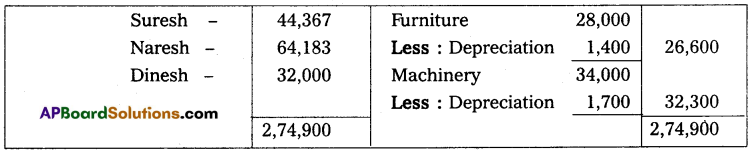
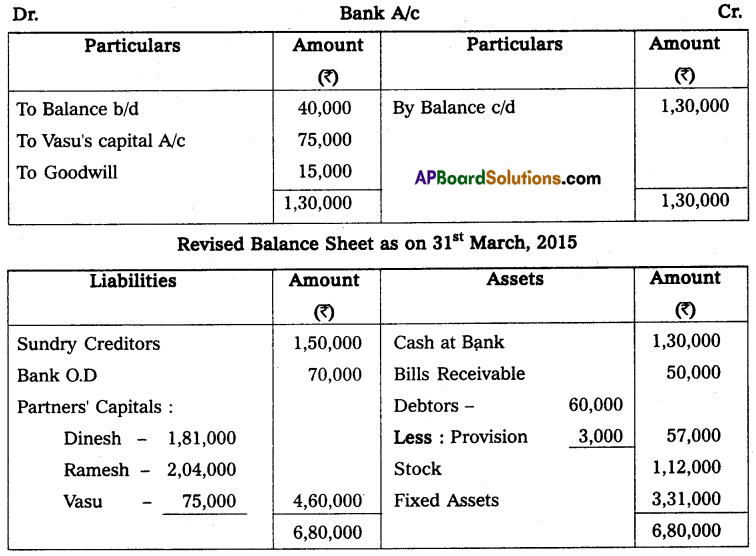
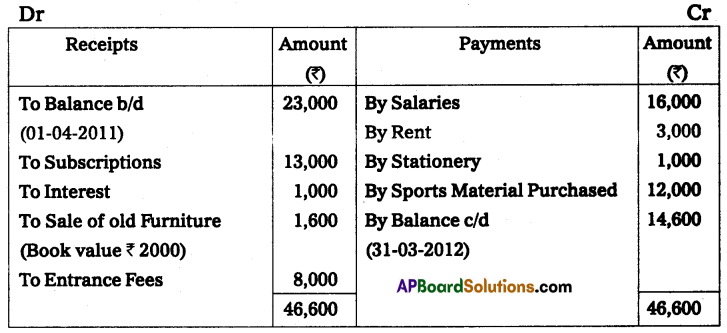
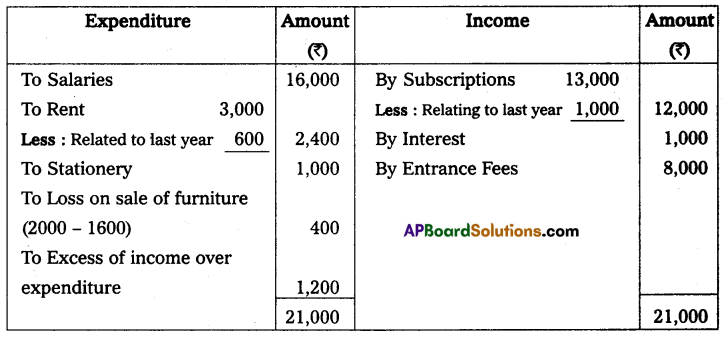
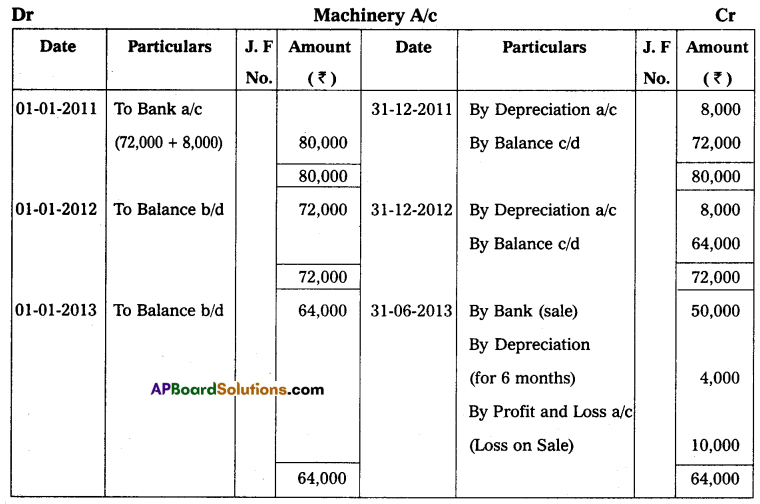
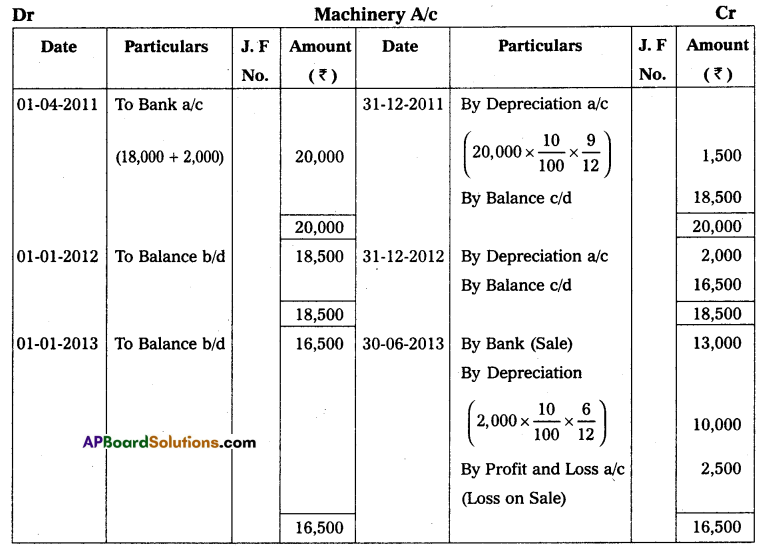
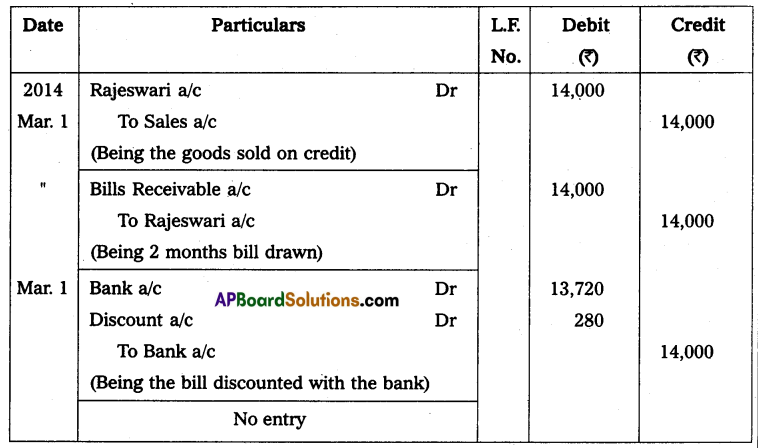
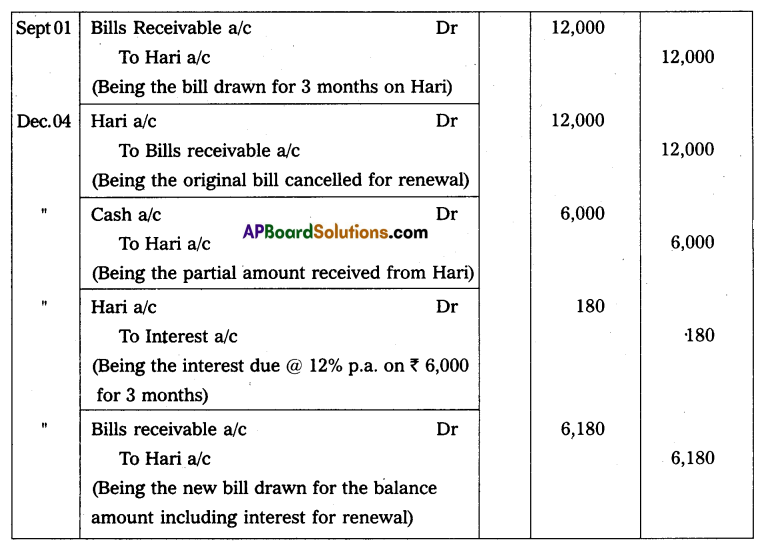
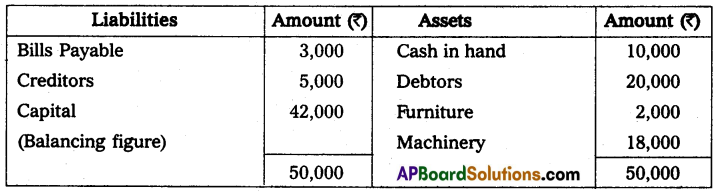
Question 10.
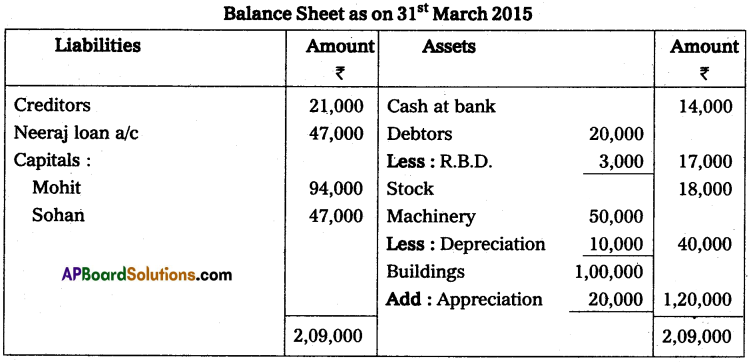
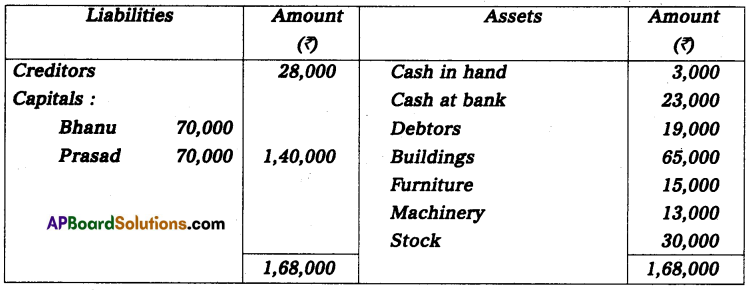
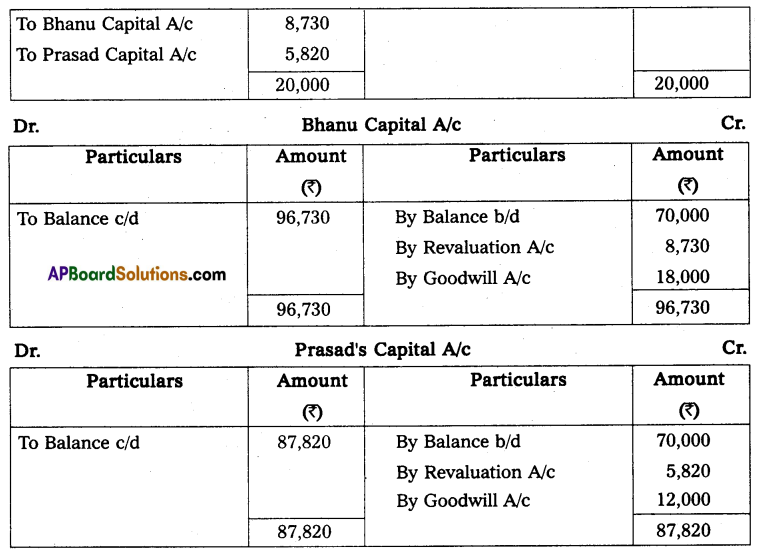
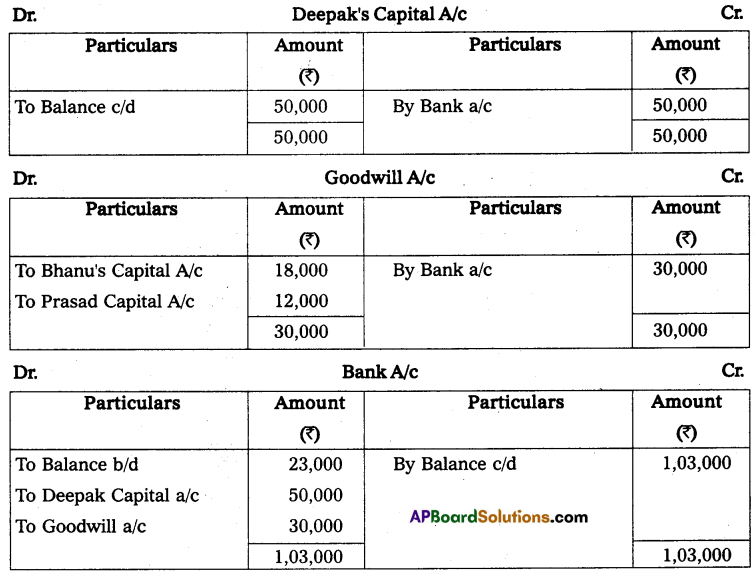
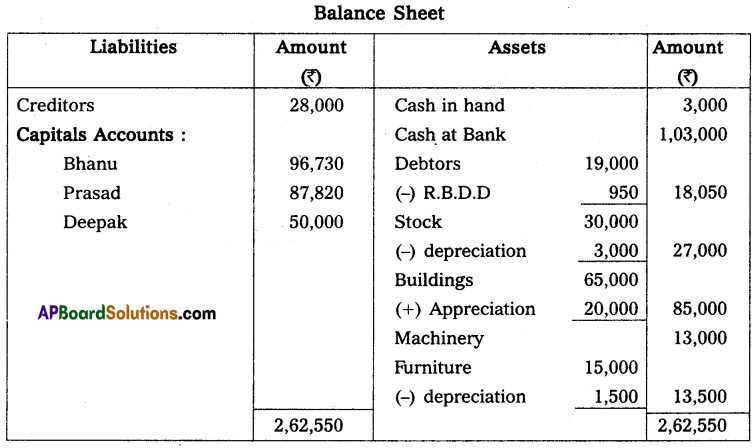
Mr. Ramesh commenced business on 1st April 2013 with a capital of ₹ 35,000. On 31st March 2014, his position was as follows.
Furniture – ₹ 2,000
Cash in hand – ₹ 10,000
Machinery – ₹ 18,000
Creditors – ₹ 5,000
Debtors – ₹ 20,000
Bills Payable – ₹ 3,000
During the year he withdrew ₹ 12,000 for his personal use and introduced additional capital ₹ 6,000 to find out the profit or loss made by Mr. Ramesh during the year.
Solution:
Statement of Affairs as of 31st March 2014
Statement showing Profit or Loss

![]()
Question 11.
Mr. Harsha maintains his books on single-entry systems he gives you the following information.
Capital on 01-04-2013 – ₹ 8,000
Capital on 31-03-2014 – ₹ 9,500
Drawings for the year – ₹ 2,000
Capital introduced during the year – ₹ 1,500
You are required to calculate the profit that Harsha earned.
Solution:
Statement showing Profit or Loss

Question 12
Mr. Ganesh maintains his books on single entry method. He gives you the following information.
Capital on 01-01-2013 – ₹ 40,000
Drawings during the year – ₹ 15,000
Capital on 31-12-2014 – ₹ 45,000
Fresh capital during the year – ₹ 6,000
Prepare the statement of profit or loss.
Solution:
Statement showing Profit or Loss

Question 13.
Mr. X keeps books in the single-entry system. Find the profit from the following particulars.
Capital on 31-03-2014 – ₹ 80,000
Capital on 1-04-2013 – ₹ 70,000
Additional capital as of 2013-2014 – ₹ 4,000
Drawings made during the year – ₹ 3,000
Solution:
Statement showing Profit or Loss

Question 14.
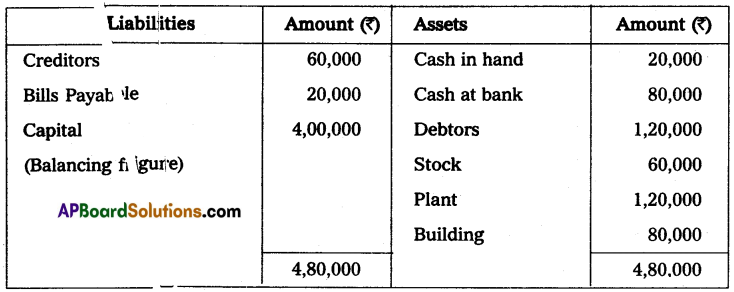
From the following details, ascertain Raju’s capital as of 01-01-2014.
Cash in hand – ₹ 20,000
Building- ₹ 80,000
Cash at Bank – ₹ 80,000
Plant – ₹ 1,20,000
Debtors – ₹ 1,20,000
Creditors – ₹ 60,000
Stock – ₹ 60,000
Bills Payable – ₹ 20,000
Solution:
Statement of Affairs as on 1-1-2014
![]()
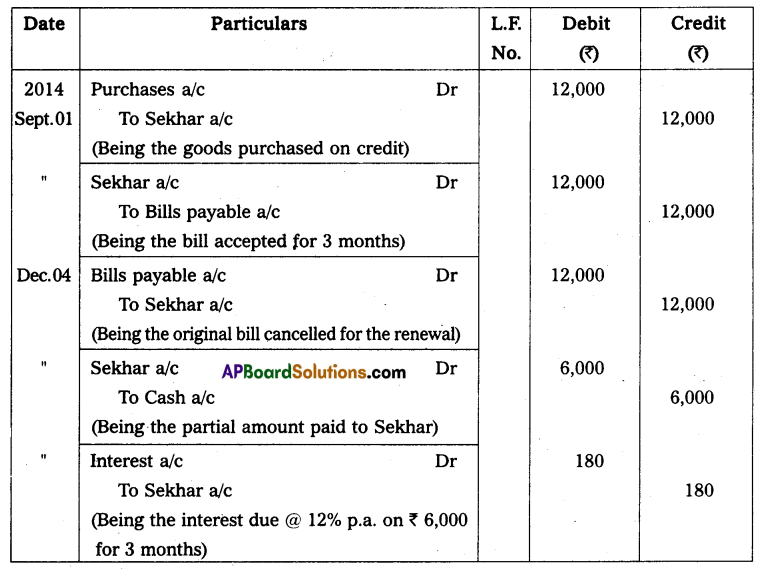
Question 15.
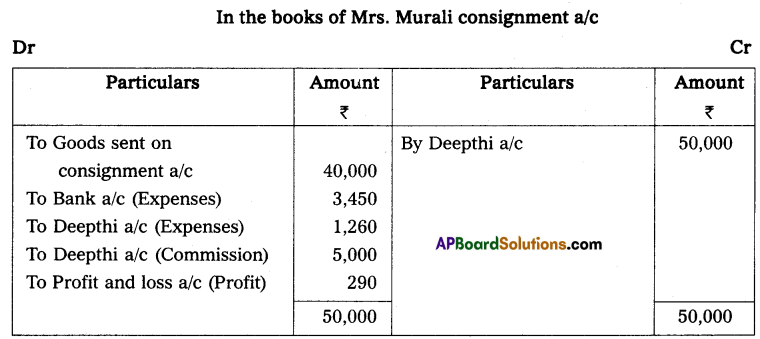
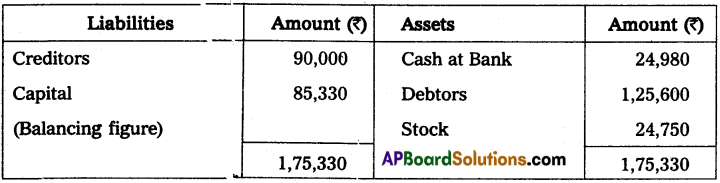
Mr. Mehta started his readymade garments business on April 1, 2013, with a capital of ₹ 50,000. He did not maintain his books according to the double entry system. During the year he introduced fresh capital of ₹ 15,000. He withdrew ₹ 10,000 for personal use. On March 31, 2014, his assets and liabilities were as follows:
Total creditors ₹ 90,000; Total debtors ₹ 1,25,600; Stock ₹ 24,750; Cash at bank ₹ 24,980.
Calculate the profit or loss made by Mr. Mehta during the first year of his business using the statement of affairs method.
Solution:
Statement of Affairs as of 31st March 2014
Statement showing Profit or Loss

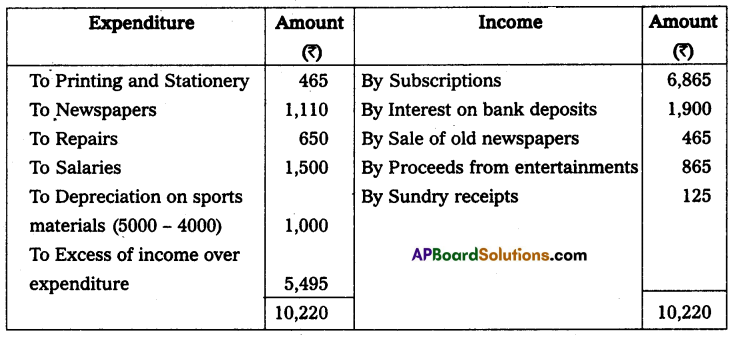
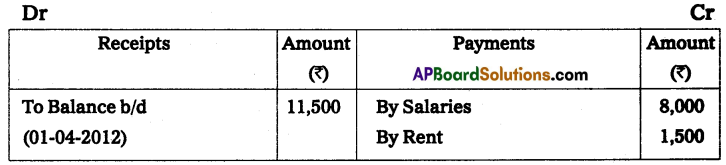
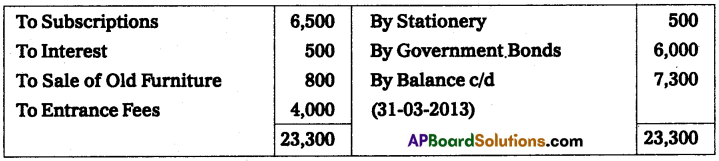
Question 16.
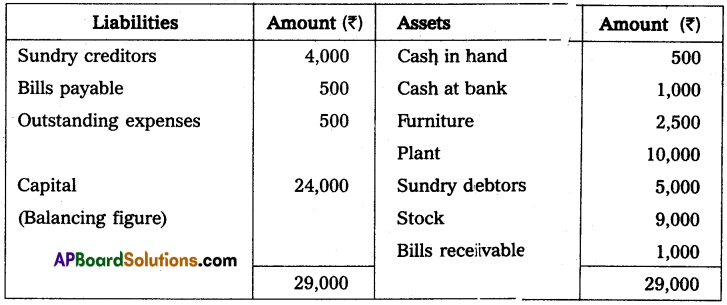
Mr. J. Keeps his books by a single entry. He started the business on 1st January 2014 with ₹ 20,000 on 31st December 2014 his position was as under.
Assets: Cash in hand ₹ 500; Cash at bank ₹ 1,000; Furniture ₹ 2,500; Plant ₹ 10,000; Sundry debtors ₹ 5,000; Stock ₹ 9,000 and Bills receivables ₹ 1,000.
Liabilities: Sunday creditors ₹ 4,000; Bills payable ₹ 500 and Outstanding expenses ₹ 500. Ascertain the profit or loss made by J.
Solution:
Statement of Affairs as on 31-12-2014
Statement showing Profit or Loss

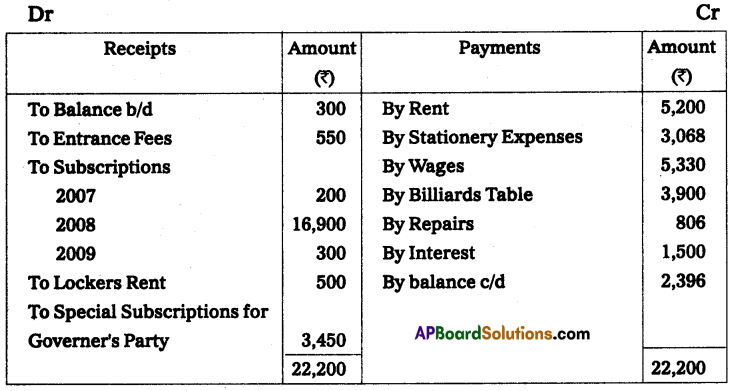
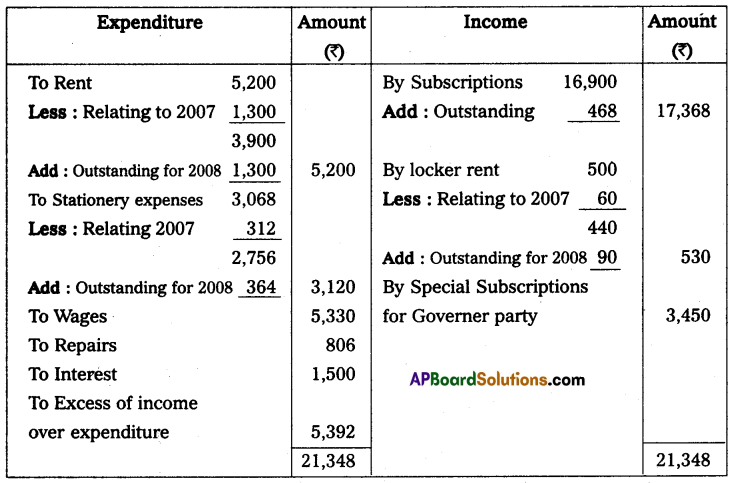
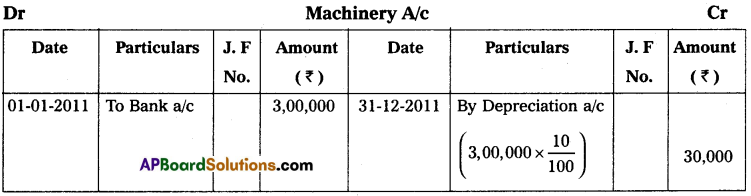
Question 17.
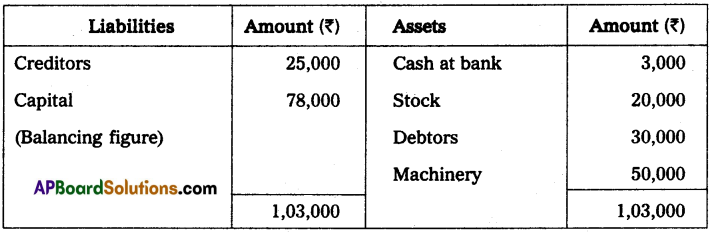
Mr. Ravikumar keeps his books on single entry his position on 31st December 2013 was as follows:
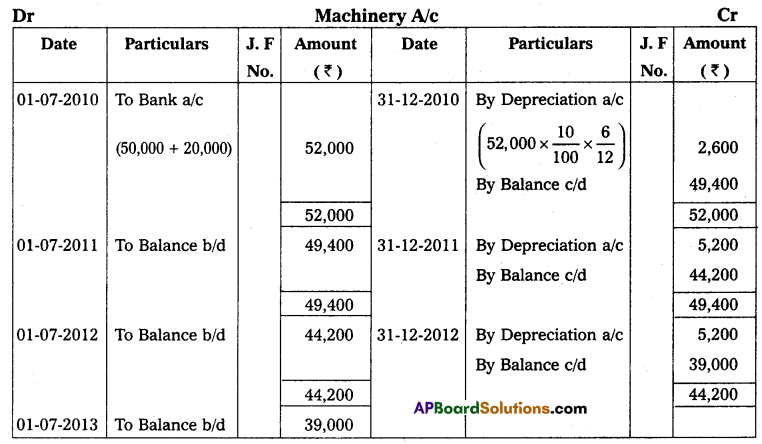
Cash at bank ₹ 3,000, Stock ₹ 20,000; Debtors ₹ 30,000, Machinery ₹ 50,000 and Creditors ₹ 25,000. His position
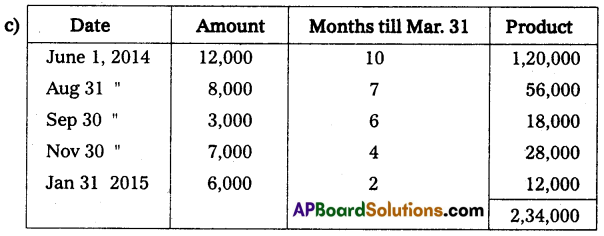
on 31st December 2014 was as follows. Cash at bank ₹ 4,000; Stock ₹ 25,000; Debtors ₹ 45,000; Machinery ₹ 50,000 and Creditors ₹ 25,000. During the year he introduced ₹ 10,000 as further capital and withdrew from business ₹ 3,000 per month.
From the above information ascertain the profit or loss made by Mr. Ravikumar for the year ended 31st December 2014.
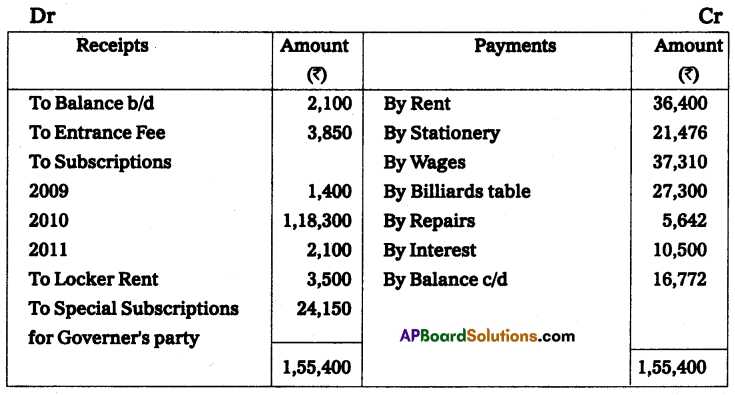
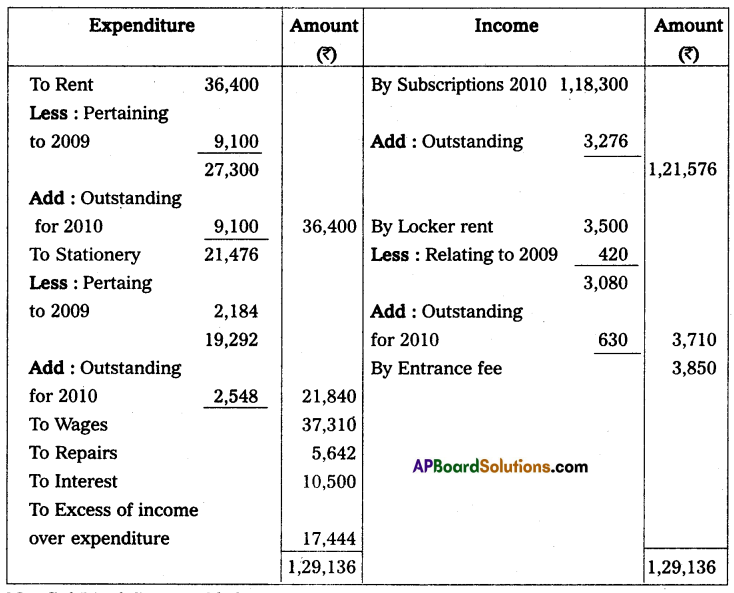
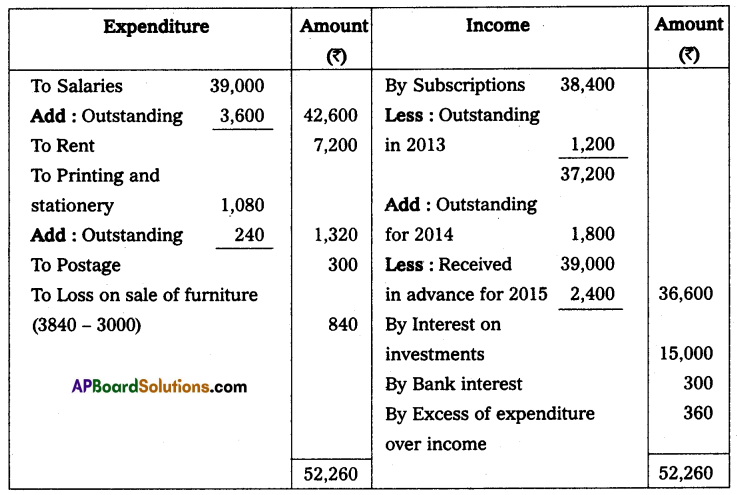
Note: Drawings ₹ 3,000 per month, per year 36,000 (3,000 × 12 months)
Solution:
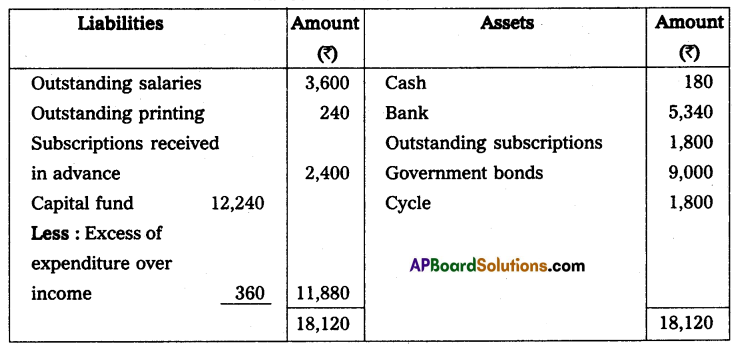
Statement of Affairs as on 31-12-2013
Statement of Affairs as on 31-12-2014
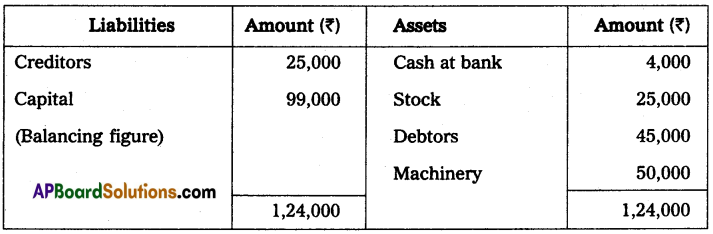
Statement showing Profit or Loss

Question 18.
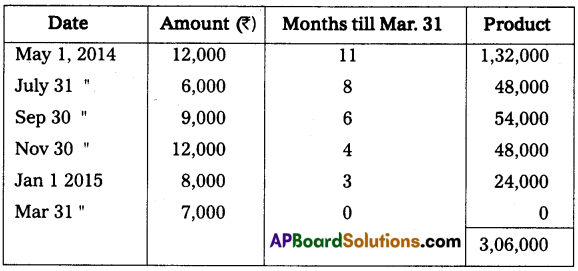
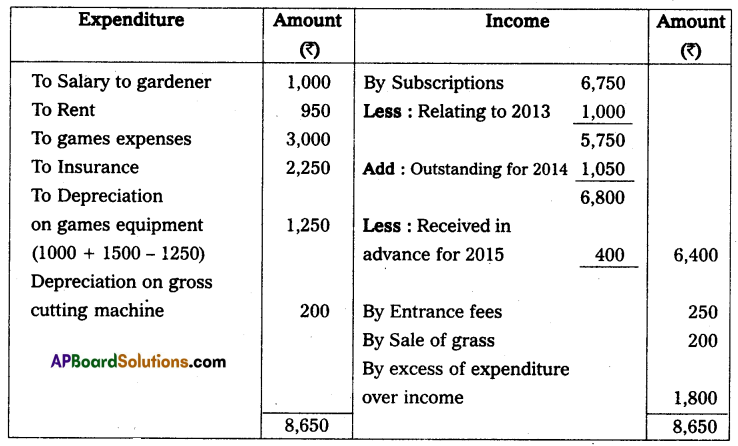
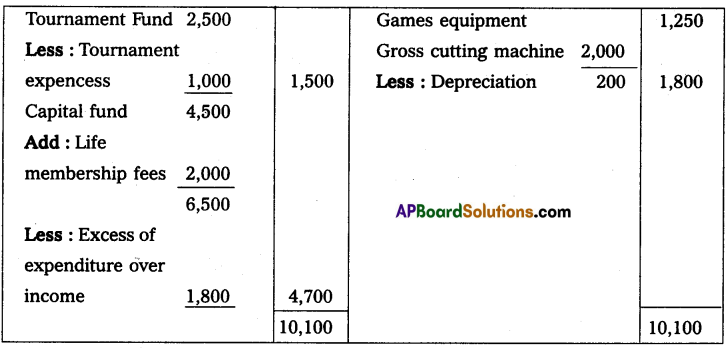
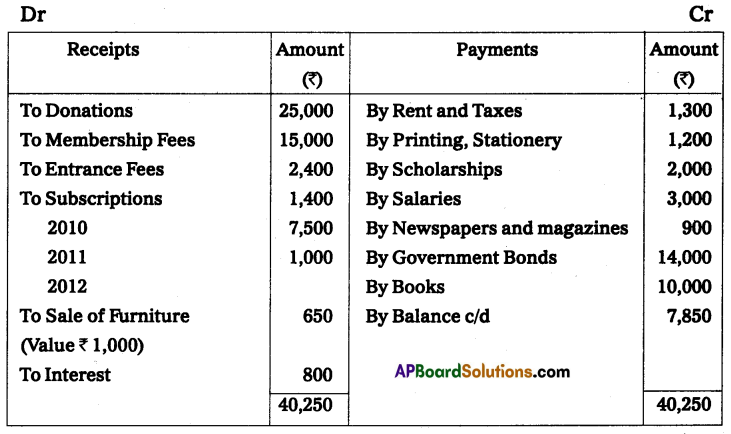
From the following particulars prepare a statement of profit and loss for the year ended 31st December 2014.
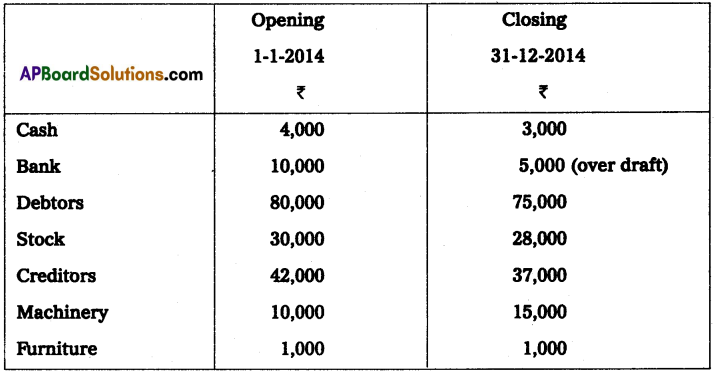
The proprietor drew at the rate of ₹ 750 per month he introduced ₹ 3,000 as fresh capital.
Solution:
Statement of Affairs as on 1-1-2014
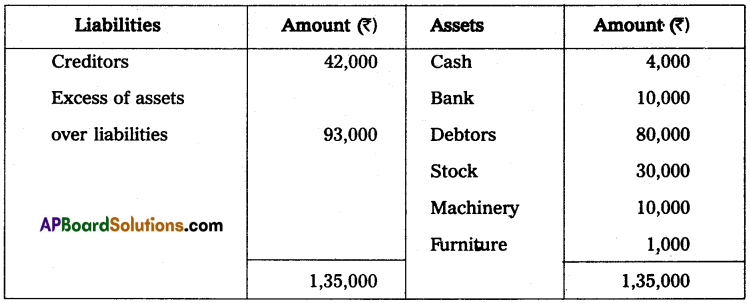
Statement of Affairs as on 31-12-2014
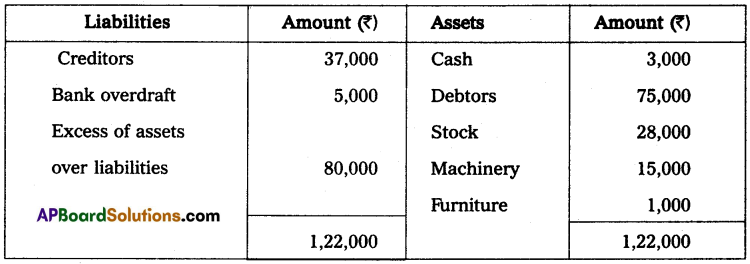
Statement showing Profit or Loss

![]()
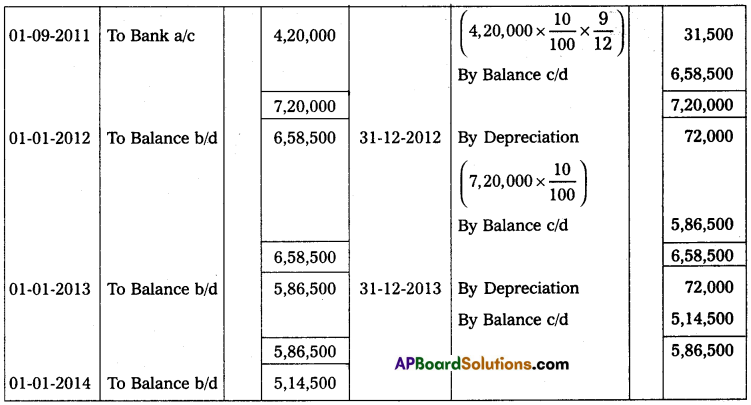
Question 19.
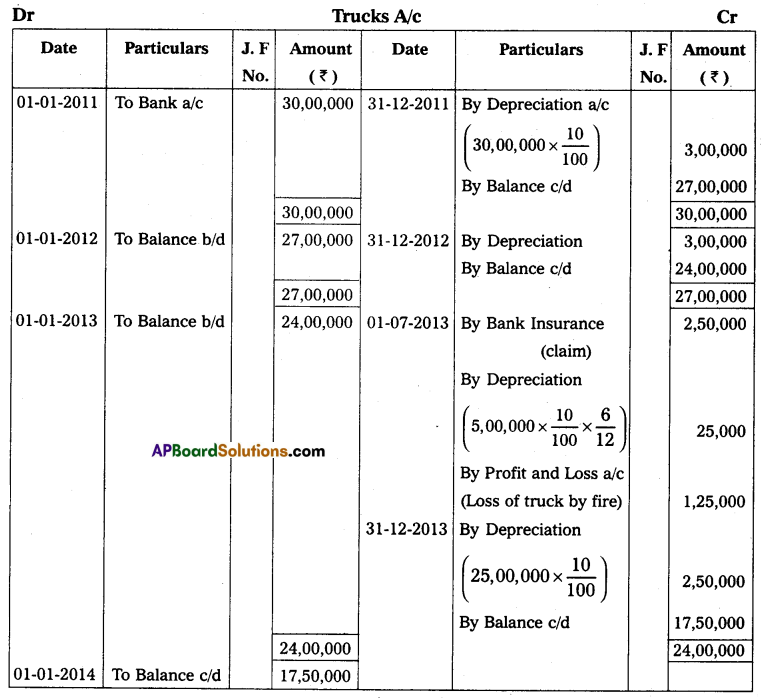
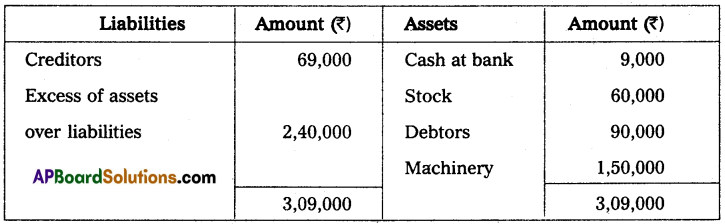
A Trader keeps his books by the single entry method. His position on 31st December 2013 is as follows. Cash at bank ₹ 9,000, Stock ₹ 60,000 Debtors ₹ 90,000, Machinery ₹ 1,50,000 and creditors ₹ 69,000. His position on 31st December 2014 was as follows. Cash at bank ₹ 12,000, Stock ₹ 75,000, Debtors ₹ 1,35,000, Machinery ₹ 1,35,000 and Creditors ₹ 75,000.
During the year the trader introduced ₹ 30,000 as further capital in the business and withdrew ₹ 900 per month. From the above, you are required to ascertain the profit or loss made by the trader for the year ended 31-12-2014.
Solution:
Statement of Affairs as on 31-12-2013
Statement of Affairs as on 31-12-2014
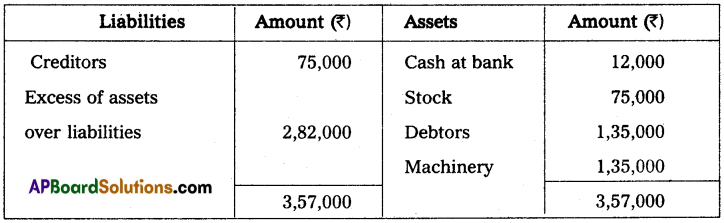
Statement showing Profit or Loss

Question 20.
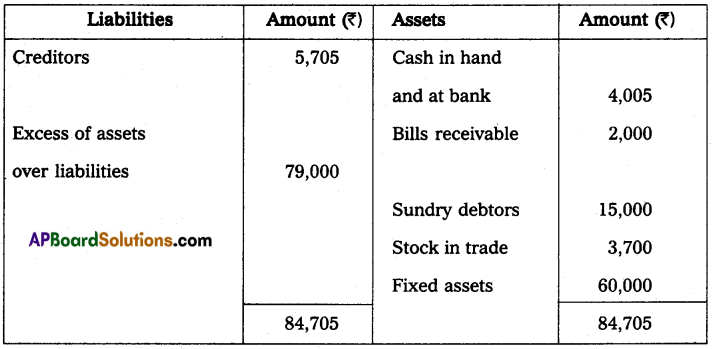
The assets and liabilities of Mr. well on 01-01-14 and 31-12-2014 were as follows.

Calculate the profit after charging interest on capital in the beginning at 5 percent per annum after providing interest on drawings at 6 percent. Drawings were ₹ 14,000
Solution:
Statement of Affairs as on 1-1-2014
Statement of Affairs as on 31-12-2014
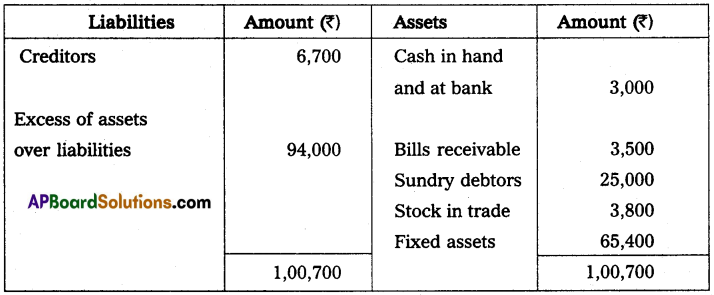
Statement showing Profit or Loss
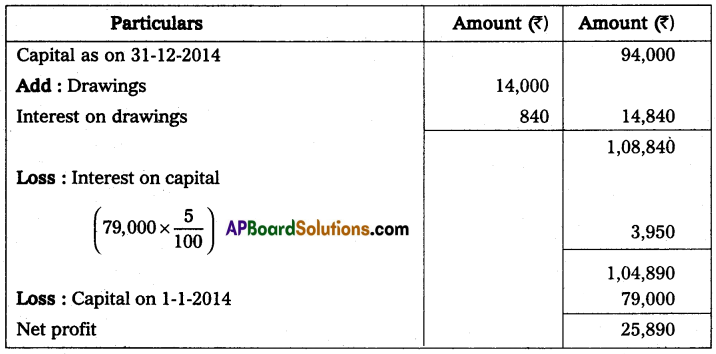
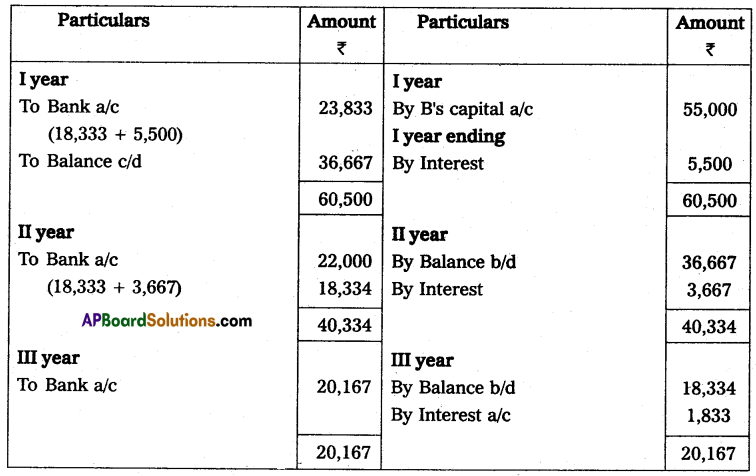
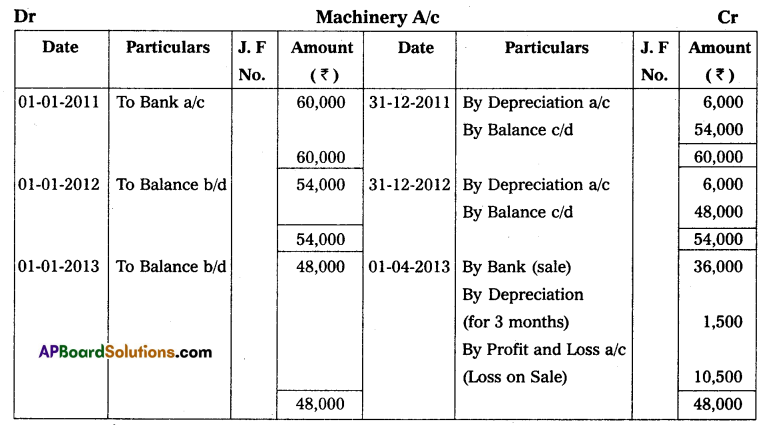
Question 21.
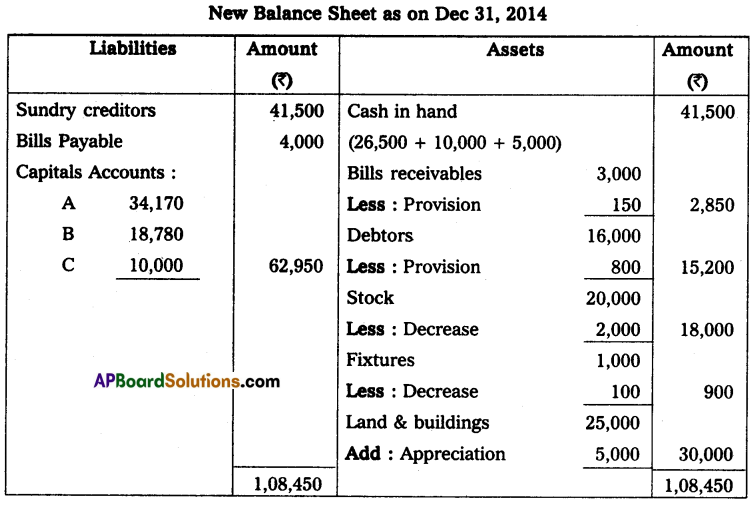
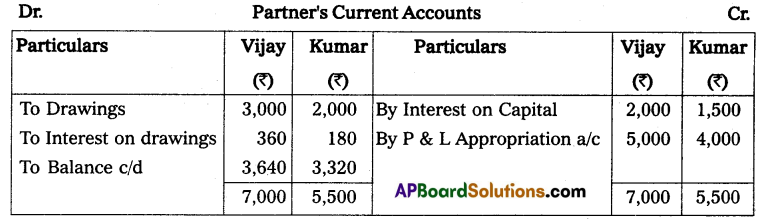
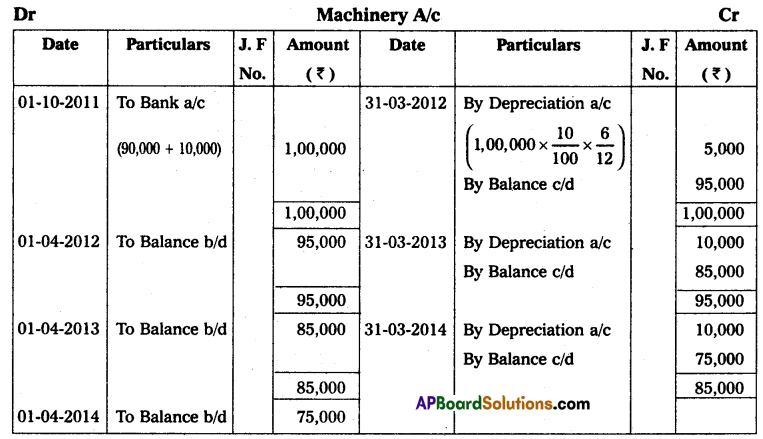
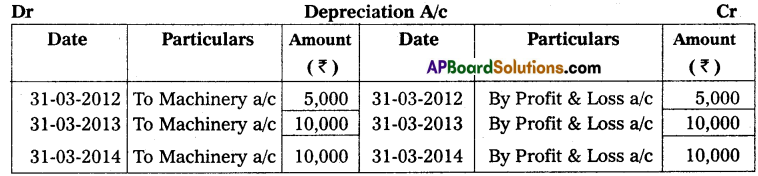
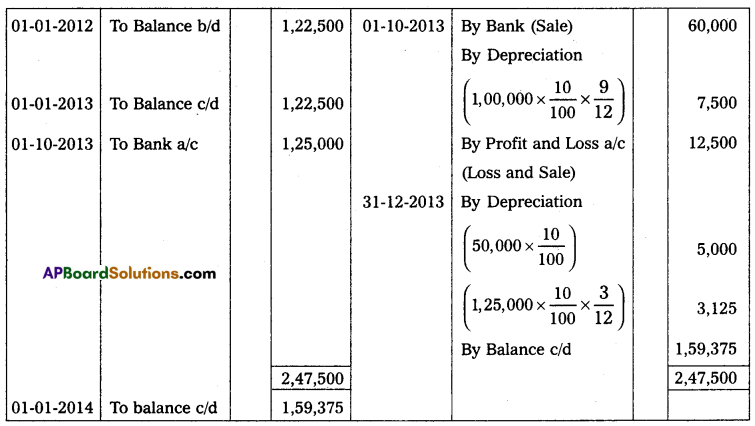
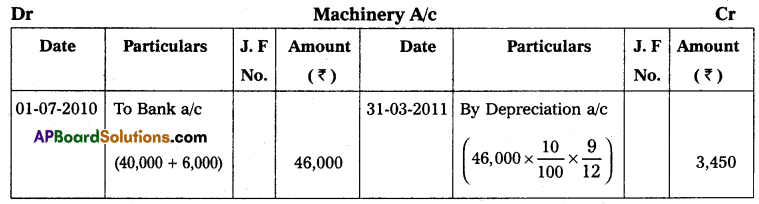
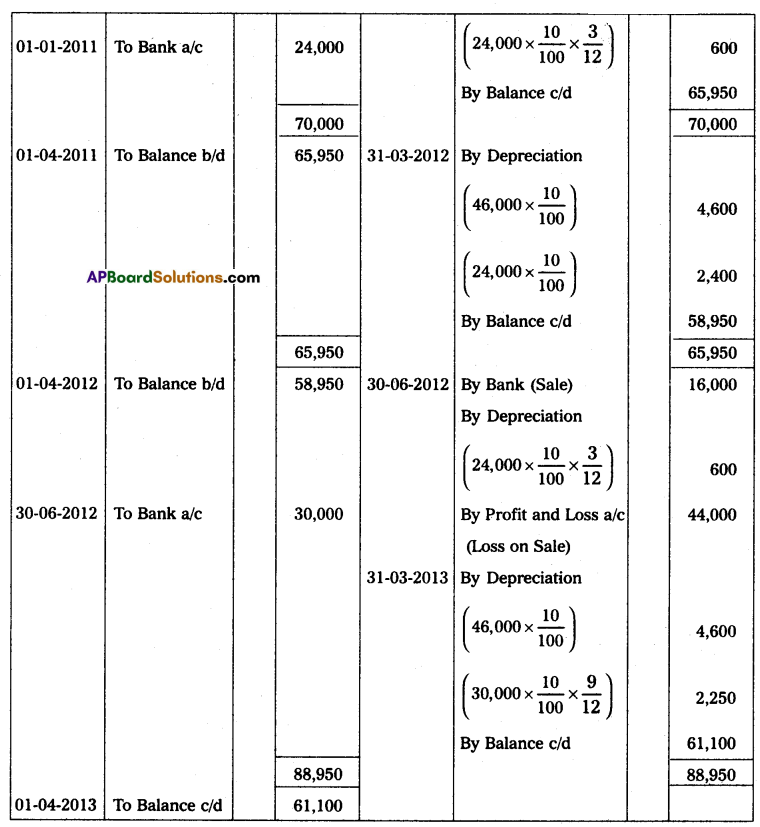
Mr. Vijay starts his business with ₹ 30,000 in cash as his capital on 1st April 2013, At the end of the year, his position was as follows. Creditors ₹ 7,500; Debtors ₹ 6,000; Cash at Bank ₹ 12,750; Stock ₹ 7,500; and Machinery ₹ 15,000. During the year he withdrew ₹ 1,125 every month. On 1st October 2013, he introduced a further capital of ₹ 7,500. You are required to ascertain the profit or loss made by him during the year after considering the following adjustments. Machinery was to depreciate at 12% and a reserve of 2% was to be raised against Debtors; Also prepare a statement of affairs on 31 March 2014.
Solution:
Statement of Affairs as on 31-3-2014


Statement showing Profit or Loss
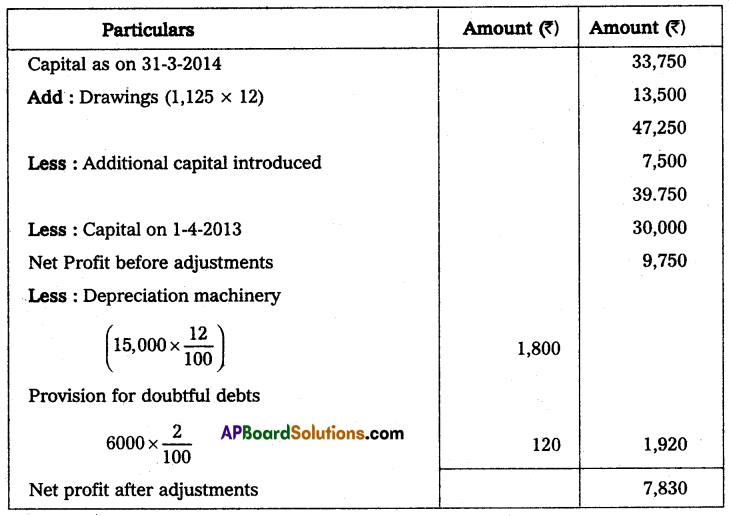
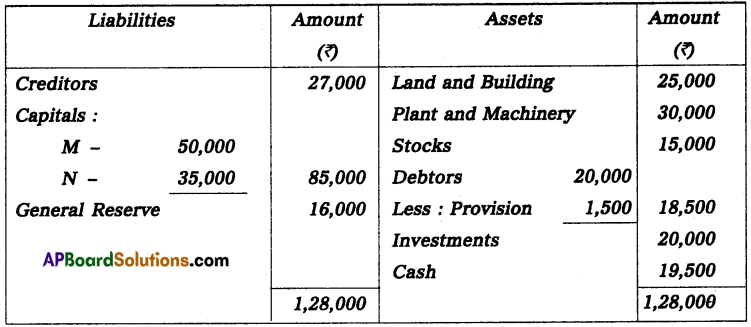
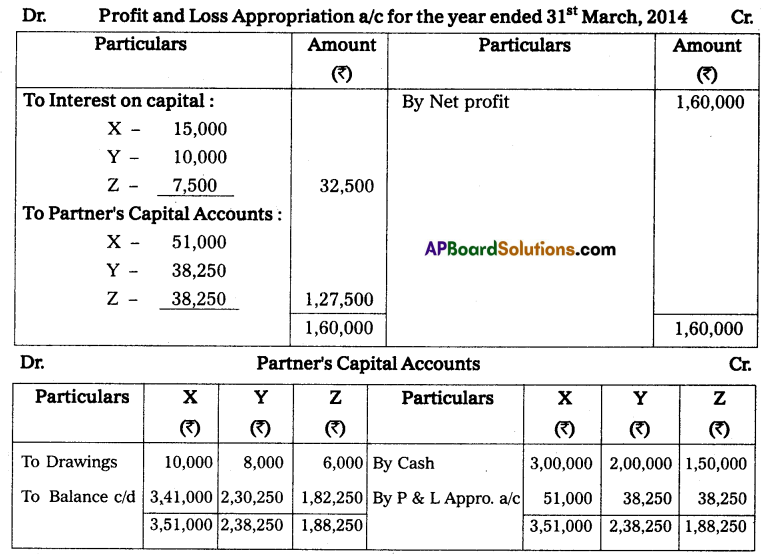
Question 22.
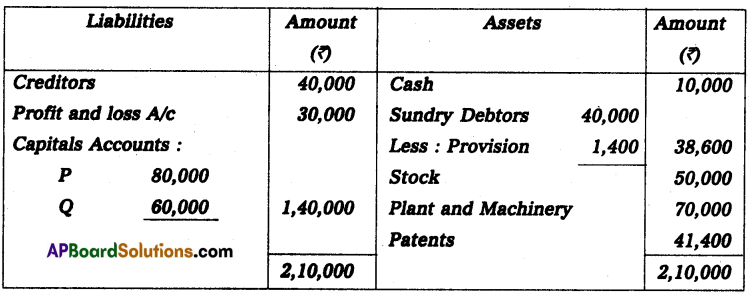
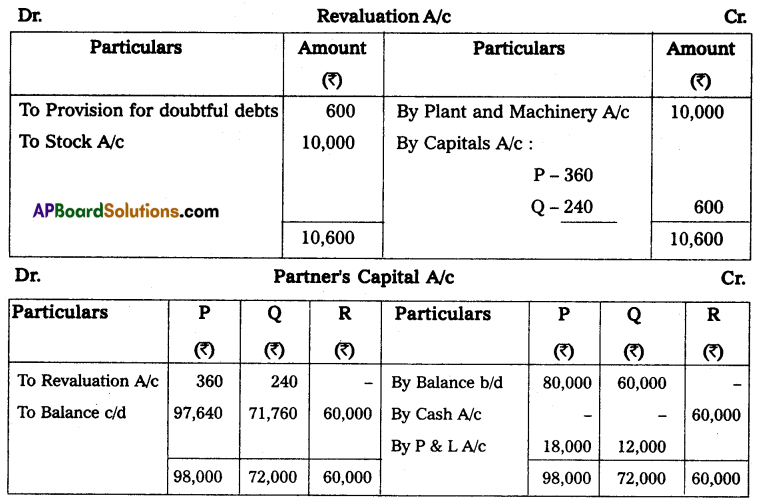
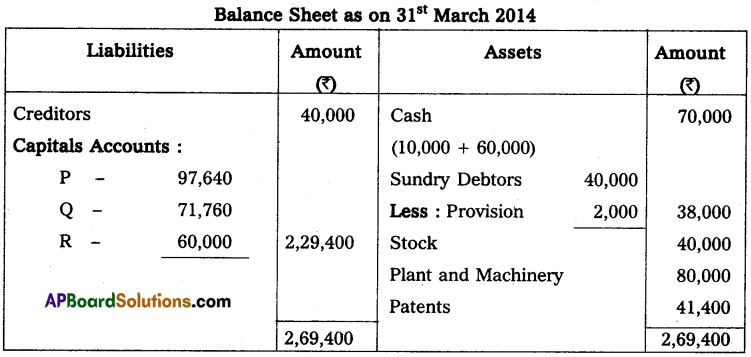
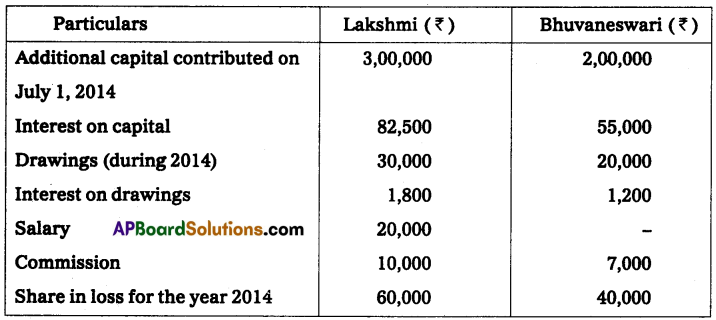
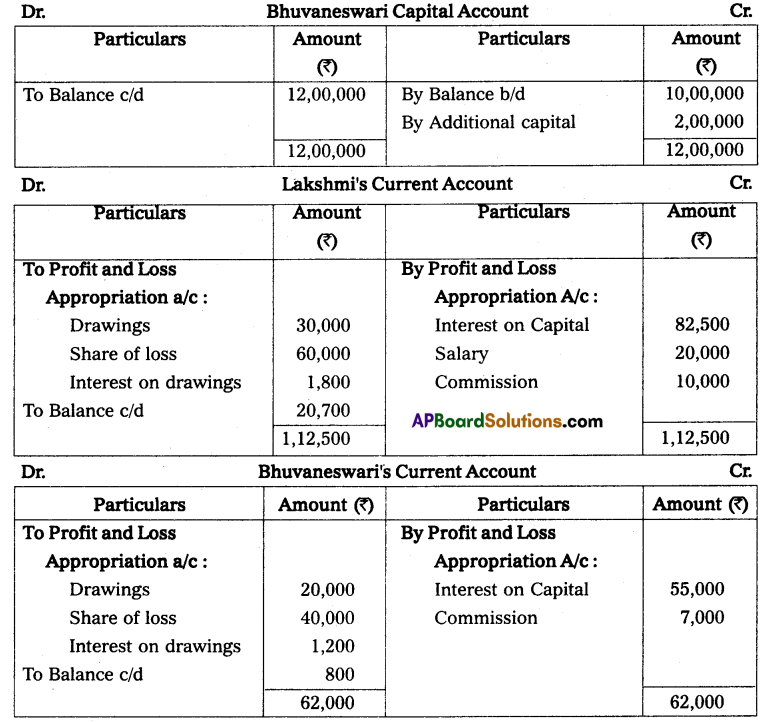
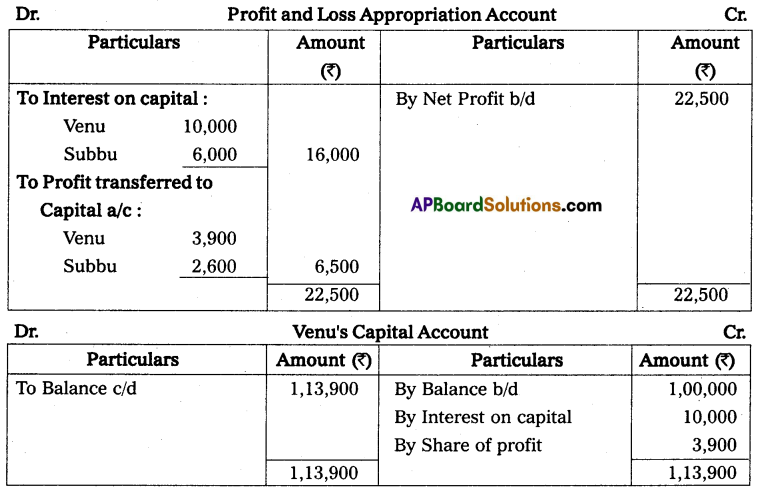
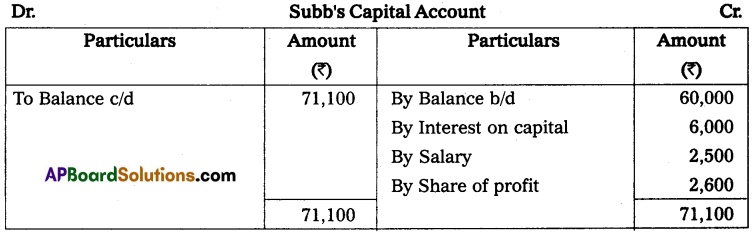
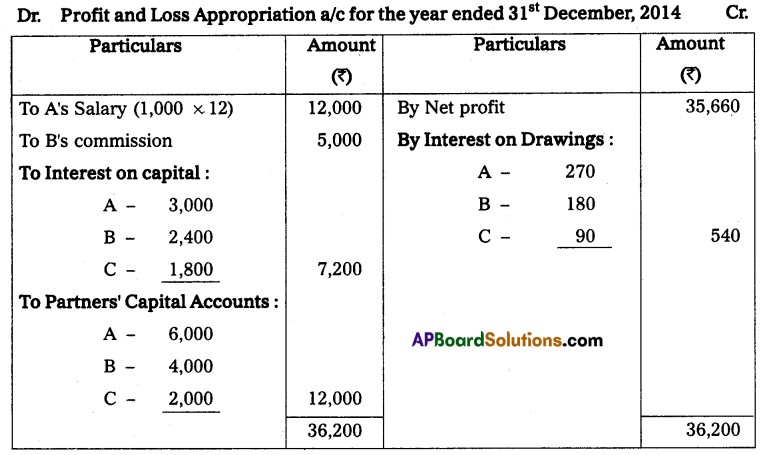
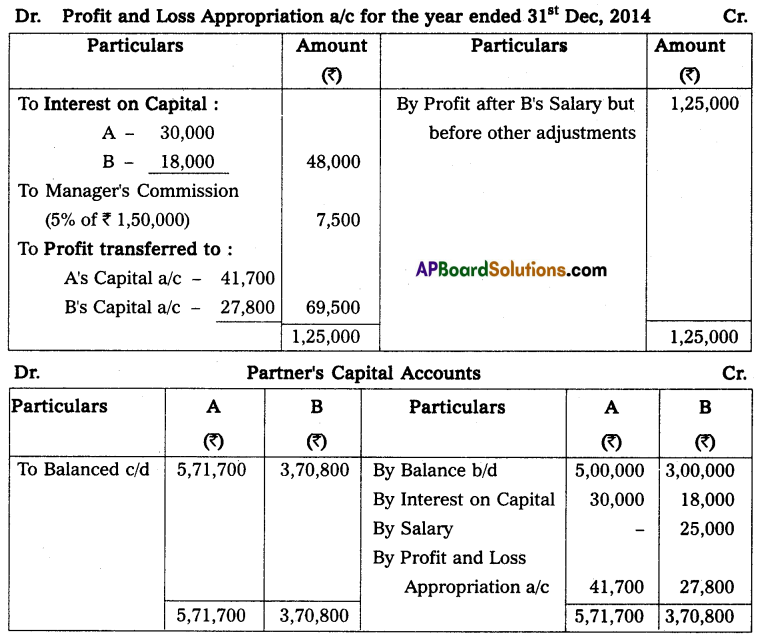
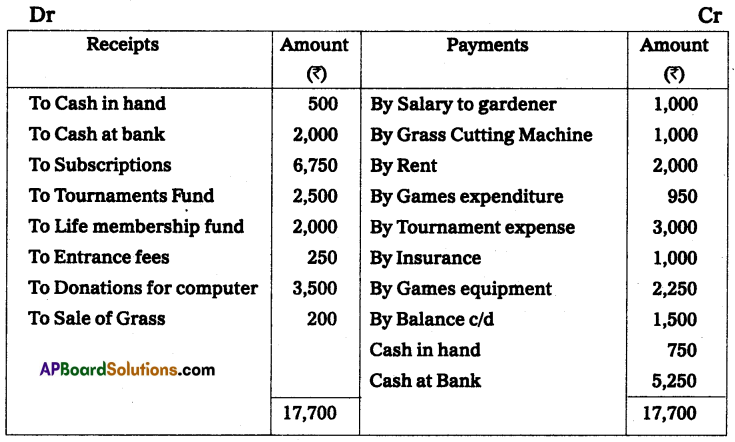
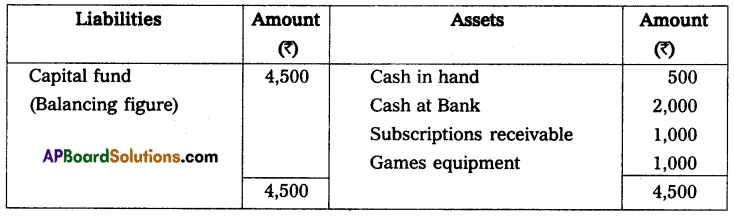
Gopal and Krishna kept their books of accounts under a single entry system. Their capital accounts on 1st April 2013 show a balance of ₹ 2,00,000 and ₹ 1,00,000 respectively. The net profits are to be shared as Gopal 2/3 and Krishna 1/3. During the year they have withdrawn ₹ 10,000 and ₹ 7,500. On March 2014 their assets and liabilities were as follows. Assets: Furniture ₹ 75,000; Stock ₹ 1,75,000; Debtors ₹ 1,25,000; Bills receivable ₹ 25,000; Cash at bank ₹ 10,000.
Liabilities: Sundry creditors ₹ 25,000; Bills payable ₹ 12,500.
Prepare a statement of affairs on 31st March 2014 and calculate the divisible profits of the partners.
Solution:
Statement of Affairs as on 31-3-2014


Statement of profit or loss for the year ending 31-3-2014
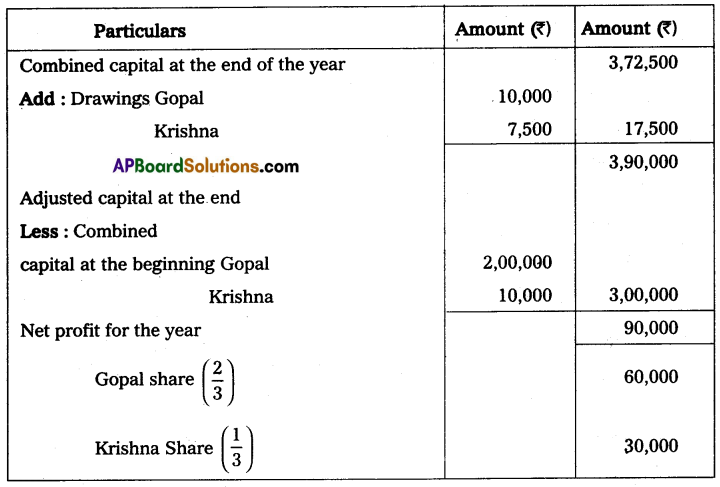
![]()
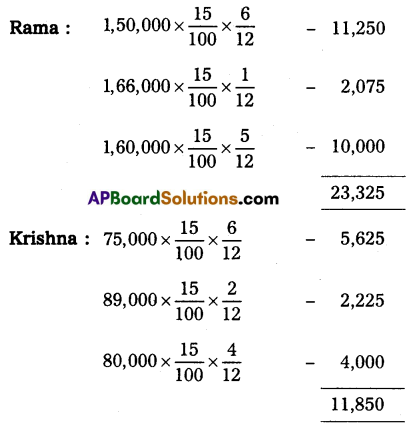
Question 23.
Ramesh and Rajesh are partners sharing the profit and losses in the ratio of 4 : 1 on 31st March 2013, their capital accounts show a credit balance of ₹ 1,00,000 and ₹ 25,000 respectively. During the year they introduced a fresh capital of ₹ 25,000 and ₹ 6,250 respectively. Also, they have withdrawn ₹ 1,875 and ₹ 625 each month respectively for their personal use. On 31st March 2014. Their business position was as follows:
Assets: Machinery ₹ 58,750; Stock ₹ 61,500; Sundry debtors ₹ 33,125; Bills receivable ₹ 5,375; Cash in hand ₹ 3,750.
Liabilities: Sundry creditors ₹ 25,000. You are asked to prepare a statement of affairs and statement of profit on 31st March 2014 and calculate the divisible profits or losses of the partners.
Solution:
Statement of Affairs as of 31st March 2014


Statement showing profit or loss for the year 2014
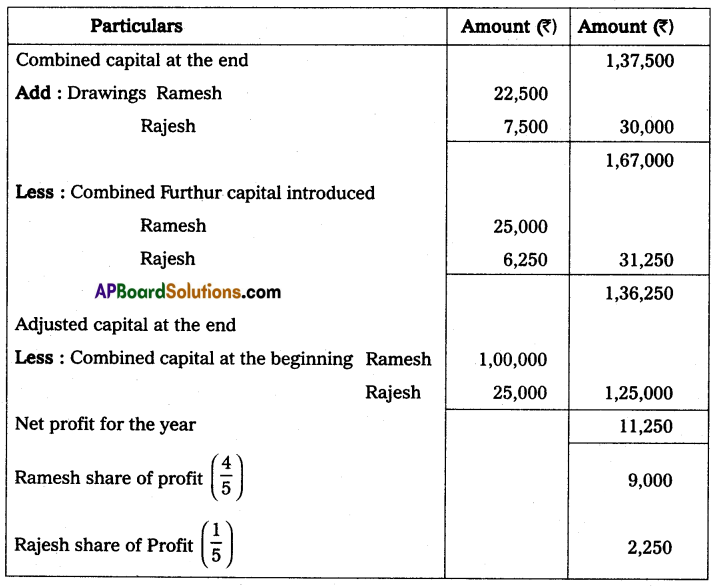
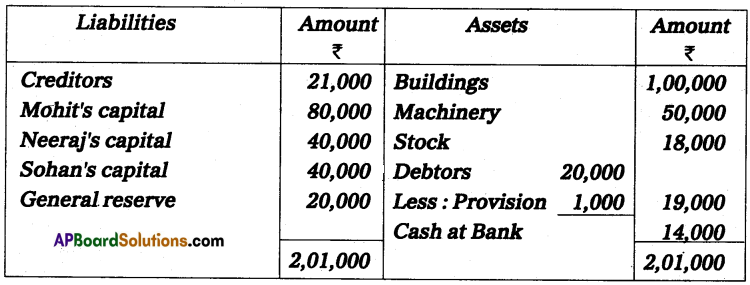
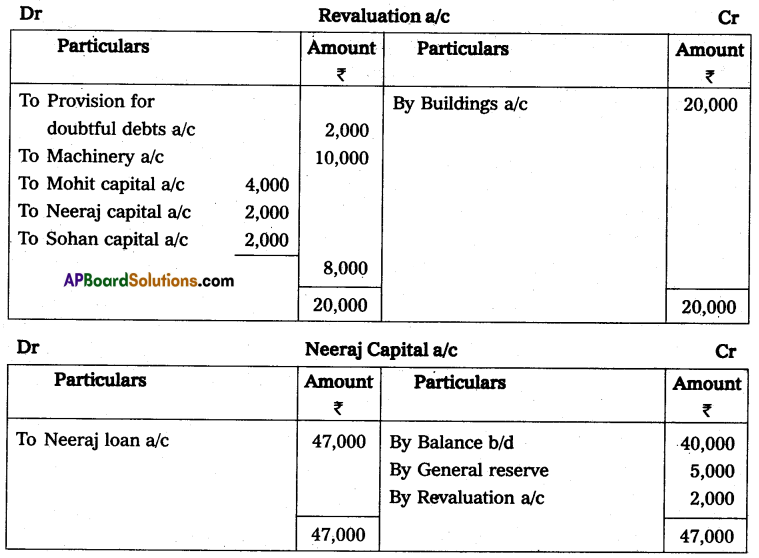
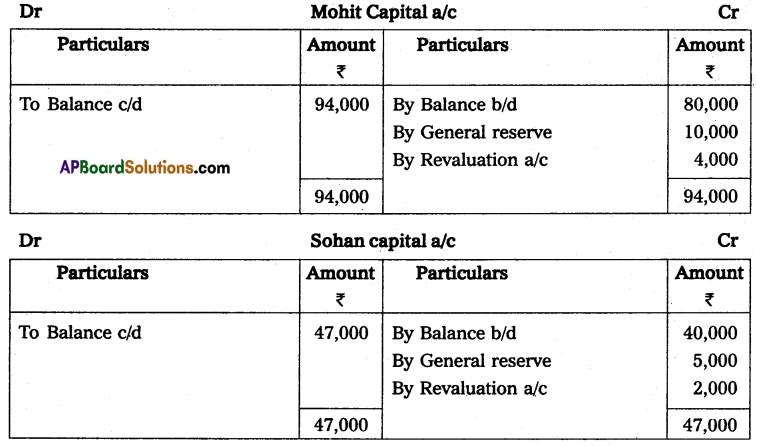
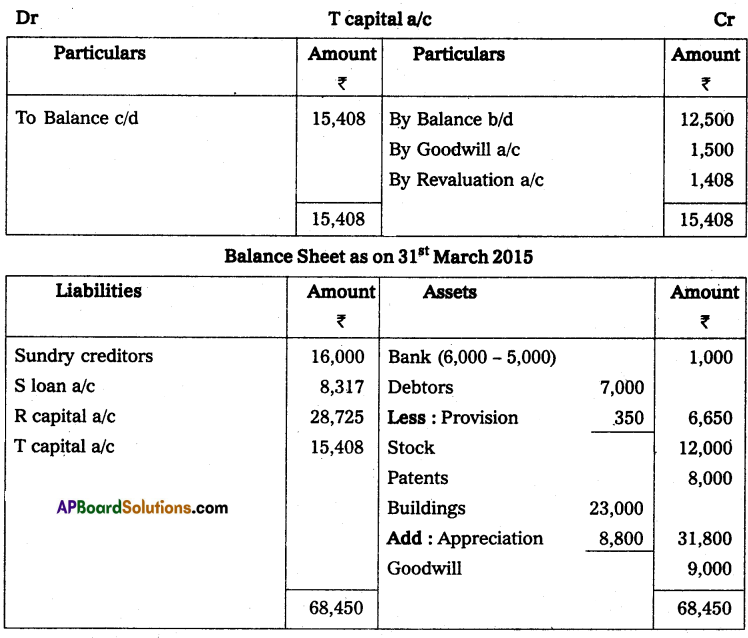
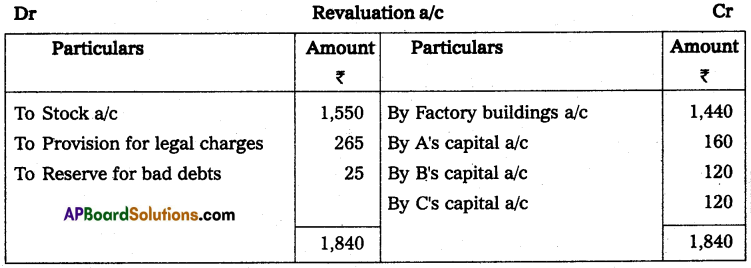
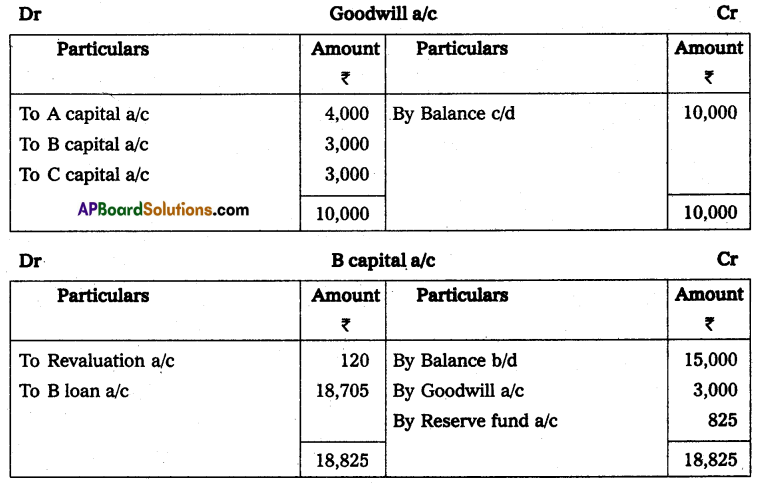
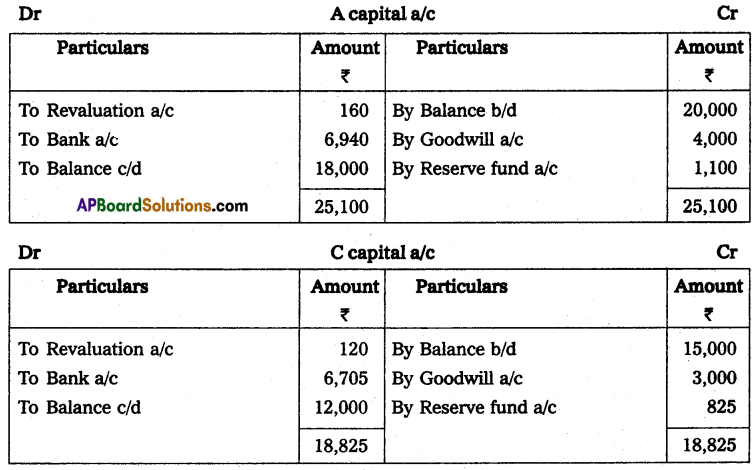
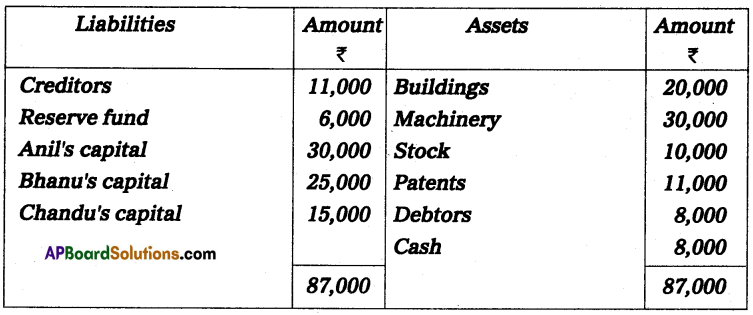
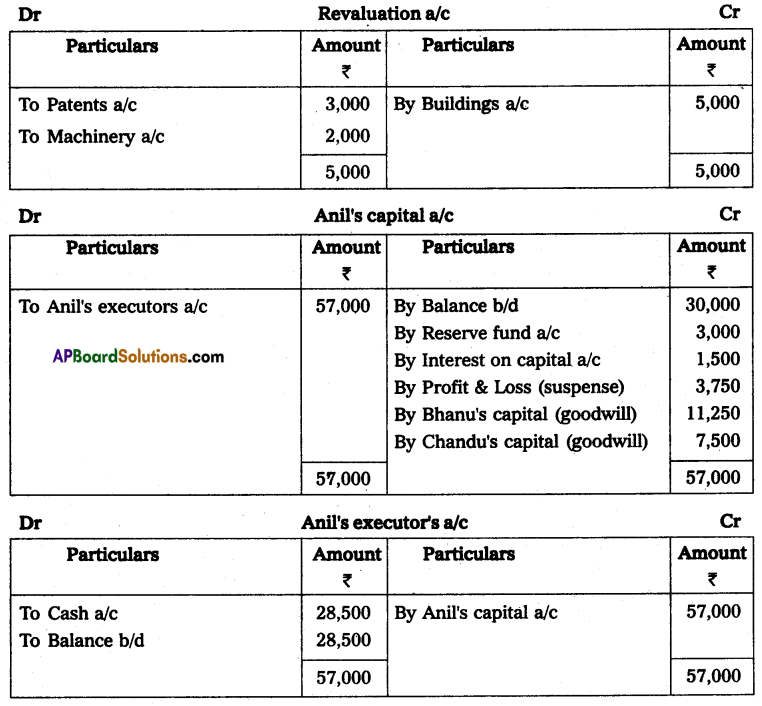
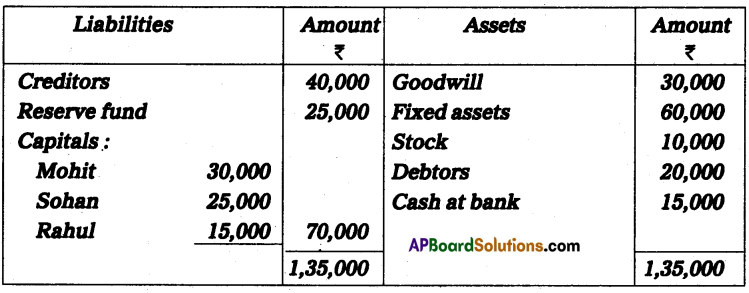
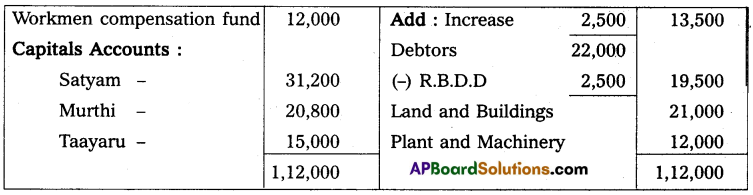
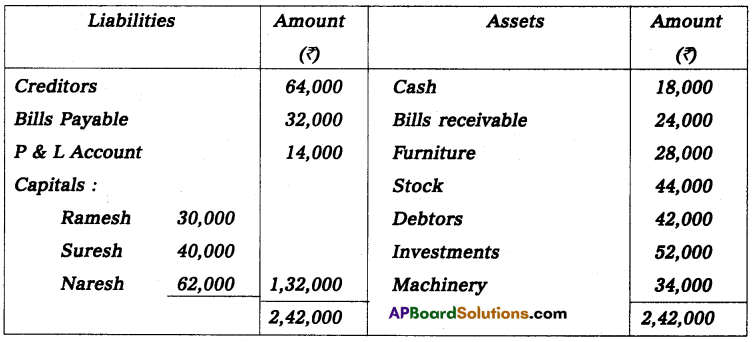
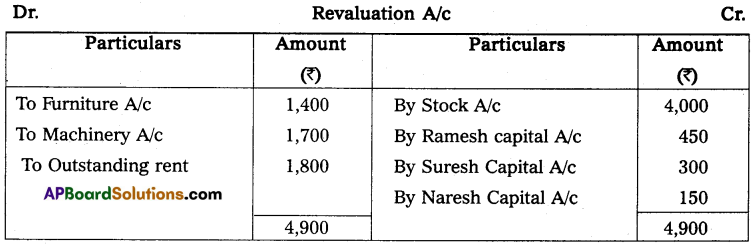
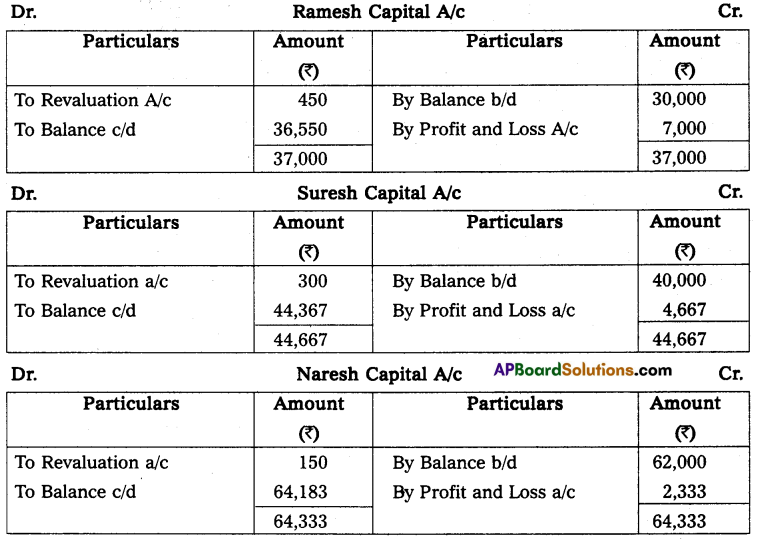
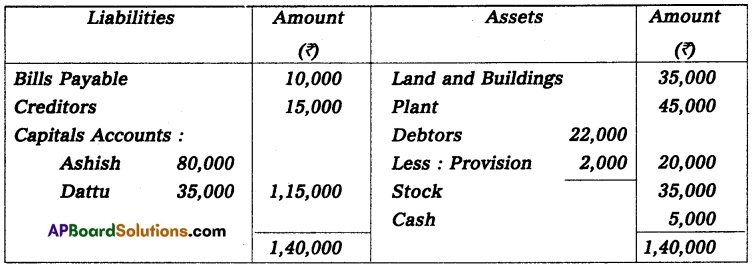
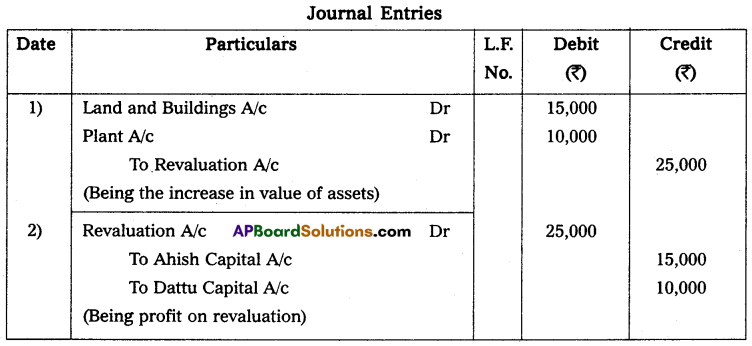
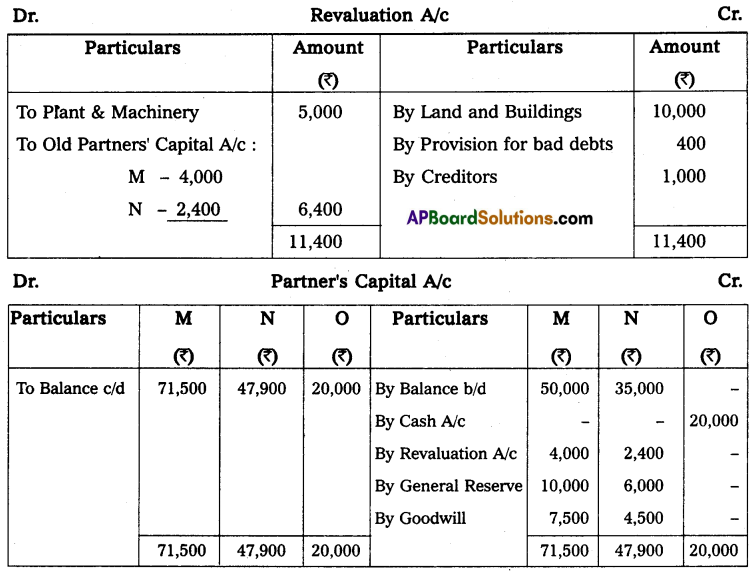
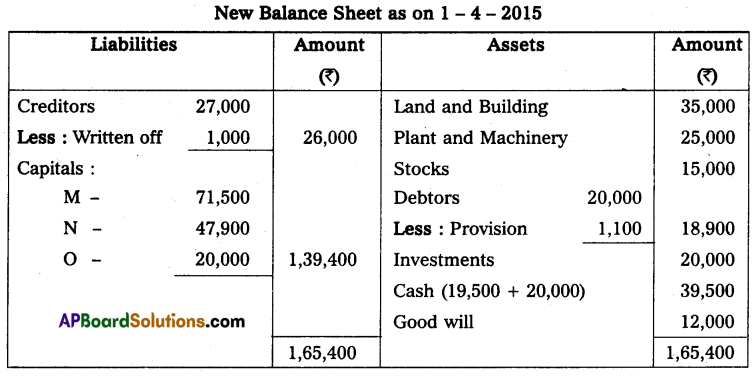
Question 24.
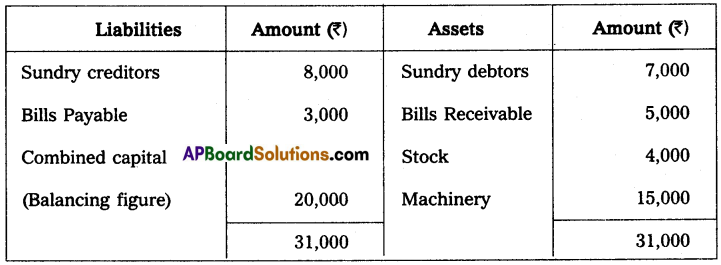
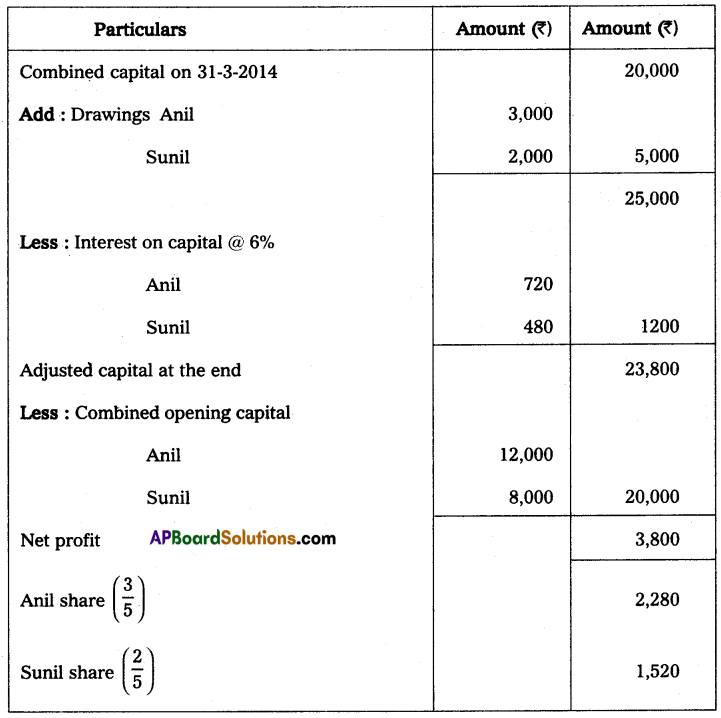
Anil and Sunil are partners sharing the profit and losses in the ratio of 3 : 2 on 31 March 2013, their capital accounts show a credit balance of ₹ 12,000 and ₹ 8,000 respectively. On 31st March 2014, their business position was as follows.
Assets: Machinery ₹ 15,000; Stock ₹ 4,000; Bills Receivables ₹ 5,000; Sundry debtors ₹ 7,000;
Liabilities: Sundry creditors ₹ 8,000; Bills payable ₹ 3,000.
You are required to prepare a profit and loss statement of affairs as of the date after taking into the following.
(a) Drawings made during the year by Anil ₹ 3,000, Sunil ₹ 2,000.
(b) Interest on capital is to be allowed at 6%.
Solution:
Statement of Affairs as on 31-3-2014
Statement showing profit or loss for the year ended 31st March 2014
Textual Examples
Question 1.
From the following information prepare the statement of affairs and find out the capital at the beginning.
Cash in Hand – ₹ 10,000
Cash in Bank – ₹ 40,000
Debtors – ₹ 60,000
Stock – ₹ 30,000
Building – ₹ 40,000
Plant – ₹ 60,000
Creditors – ₹ 30,000
Bills payable – ₹ 10,000
Solution:
Statement of affairs at the beginning
![]()
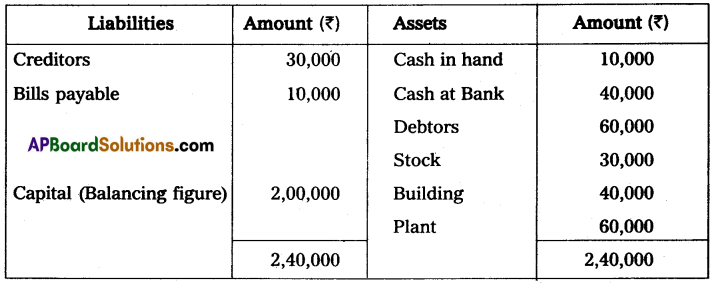
Question 2.
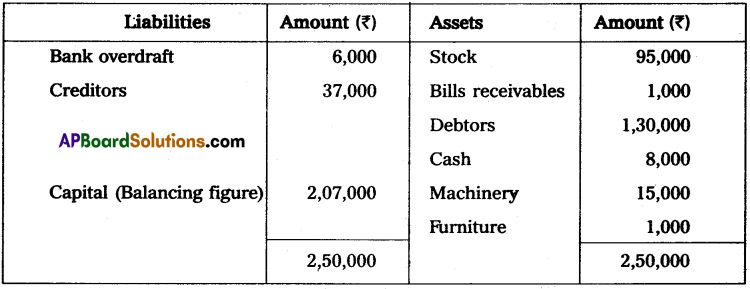
Prepare a statement of affairs from the following information and find out the capital at the end of the year.
Stock – ₹ 95,000
Debtors – ₹ 1,30,000
Cash – ₹ 8,000
Bills receivables – ₹ 1,000
Bank overdraft – ₹ 6,000
Creditors – ₹ 37,000
Machinery – ₹ 15,000
Furniture – ₹ 1,000
Solution:
Statement of affairs at the end of the year
Question 3.
From the following information compute the net profit of a trader under a single entry.
Capital at the beginning of the year – ₹ 1,00000
Capital at the end of the year – ₹ 1,50,000
Solution:

Question 4.
Compute the net profit for the year ending 31-03-2014 from the information given below.
Capital as of 1-4-2013 – ₹ 80,000
Capital as on 31-3-2014 – ₹ 75,000
Solution:
Statement of profits or loss

Question 5.
The following information is given below to prepare the statement of profit or loss.
Capital at the beginning of the year, i.e., April 01, 2013 – ₹ 7,50,000
Capital at the end of the year, i.e., March 31, 2014 – ₹ 5,00,000
Capital brought in by the proprietor during the year – ₹ 50,000
Withdrawals by the proprietor during the year – ₹ 3,75,000
Solution:
Statement of profit or loss for the year ended on March 31, 2014

![]()
Question 6.
Find out the missing value.
Capital at the beginning of the year – ₹ 30,000
Capital at the end of the year – ₹ 45,000
Drawings – ₹ 5,000
Profit – ₹ 4,000
Additional capital brought in?
Solution:

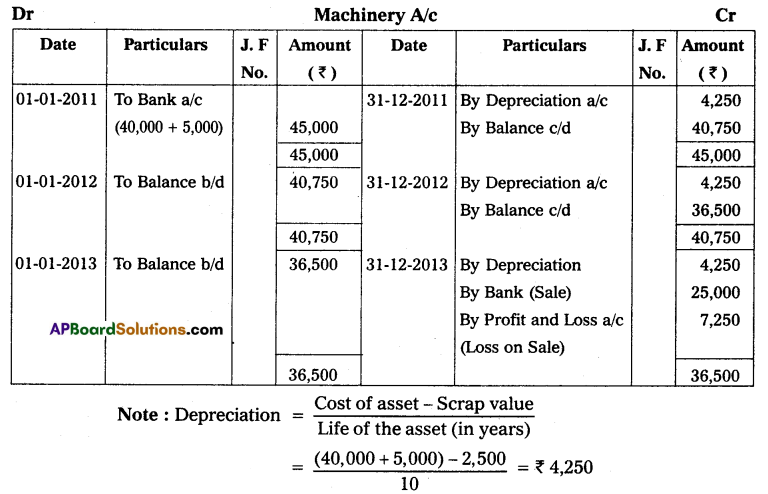
Question 7.
Gopal started his business on January 01, 2014, with a capital of ₹ 4,50,000 on December 31, 2014, his position was as under.
Cash – ₹ 99,000
Bills Receivables – ₹ 75,000
Plant – ₹ 48,000
Land and Building – ₹ 1,80,000
Furniture – ₹ 50,000
Creditors – ₹ 30,000
He owned ₹ 45,000 from his friend Sukumar on that date. He withdrew ₹ 8000 per month for his household purposes. Ascertain his profit or loss for this year ended December 31, 2014.
Solution:
Books of Mr. Gopal’s Statement of affairs as on December 31, 2014
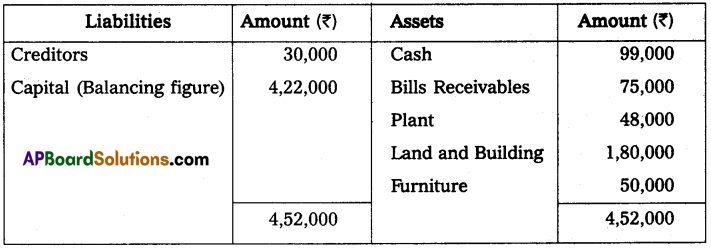
Statement of profit or loss for the year ended December 31, 2014

Note: Drawing per month (₹ 8,000 × 12 = ₹ 96,000).
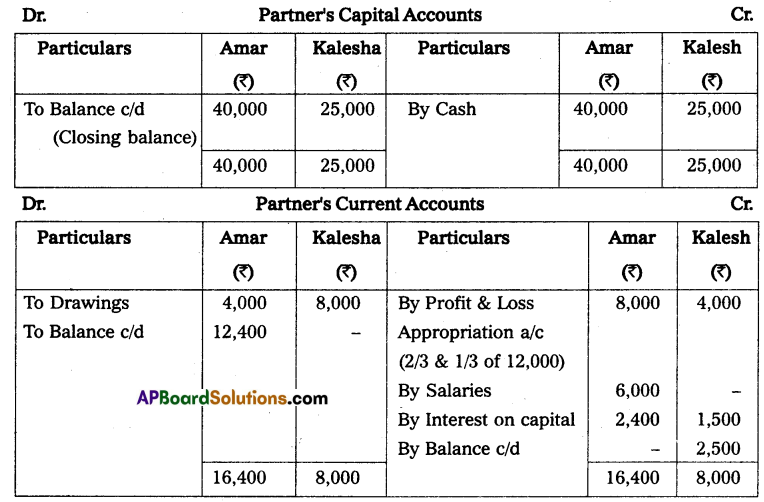
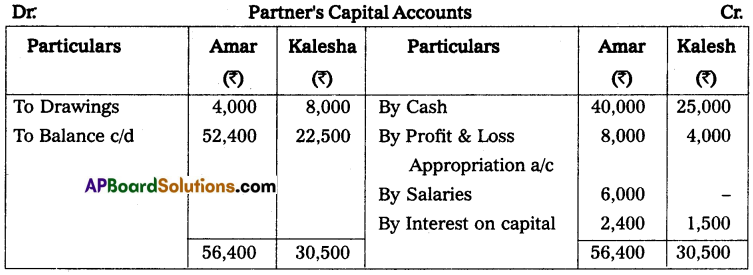
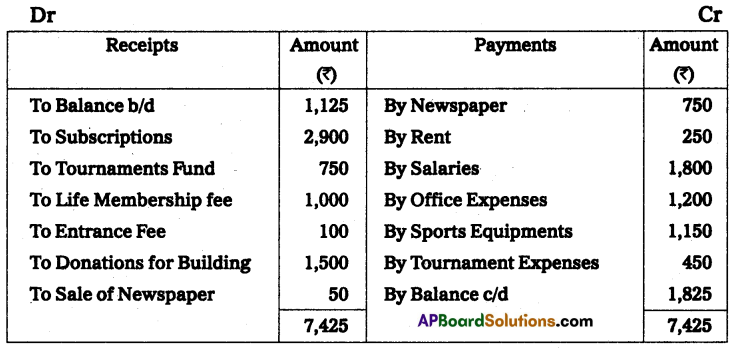
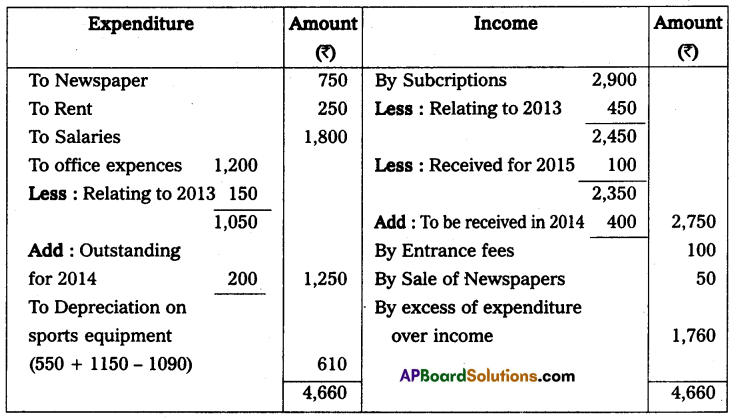
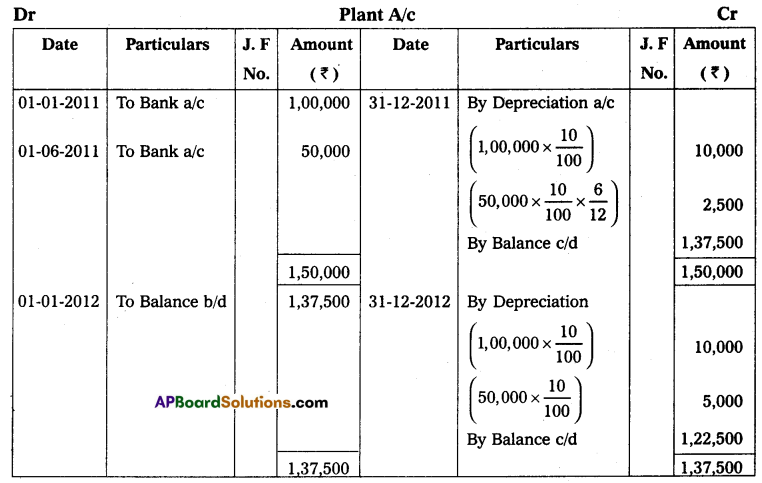
Question 8.
Mr. Ashok keeps his books on incomplete records following information is given below.
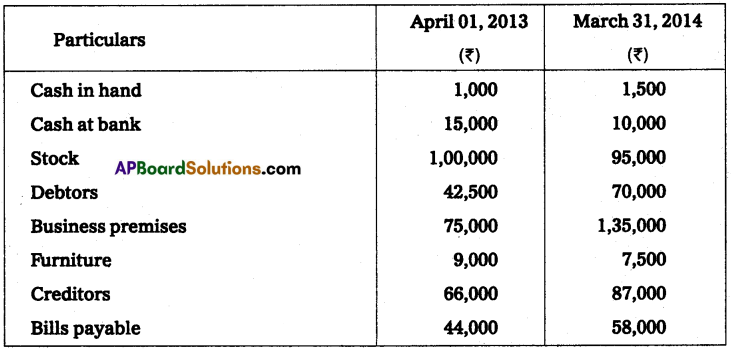
During the year he withdrew ₹ 45,000 and introduced ₹ 25,000 as further capital in the business to compute the profit or loss of the business.
Solution:
Books of Mr. Ashok Statement of affairs as on April 01, 2013, and as on March 31, 2014
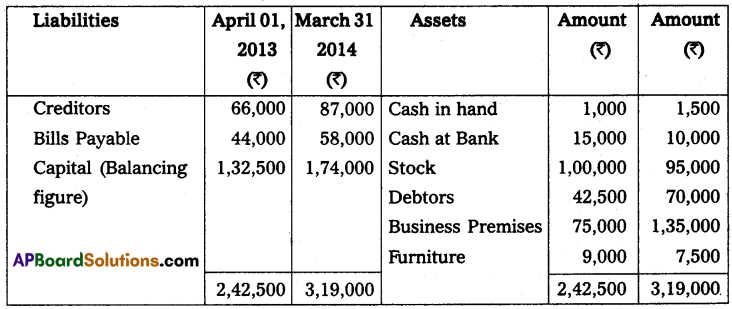
Statement of profit or loss for the year ended on March 31, 2014

![]()
Question 9.
Mr. Shankar keeps his books under single-entry system and the following information is available from his records.
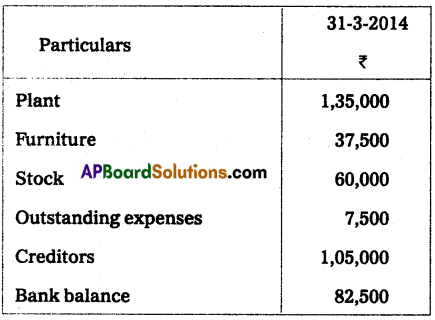
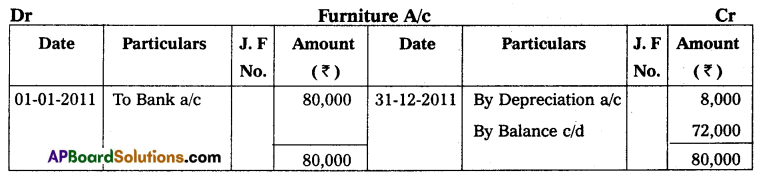
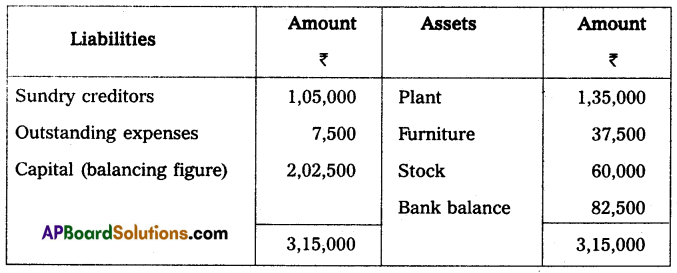
Shankar commenced business on 1st April 2013 with a capital of ₹ 1,27,000. During the year he withdrew ₹ 750 per month for his personal use. Charge depreciation on the plant at 10% and on furniture at 5% you are required to prepare a statement showing profit or loss for the year ended 31-3-2014.
Solution:
Statement of affairs as of 31-03-2014 (Before adjustments)
Statement of profit or loss for the year ended 31-03-2014

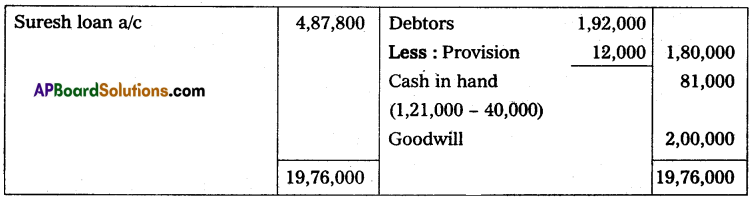
Question 10.
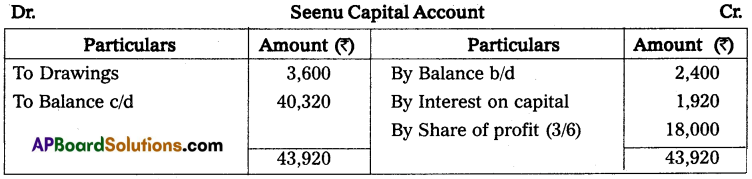
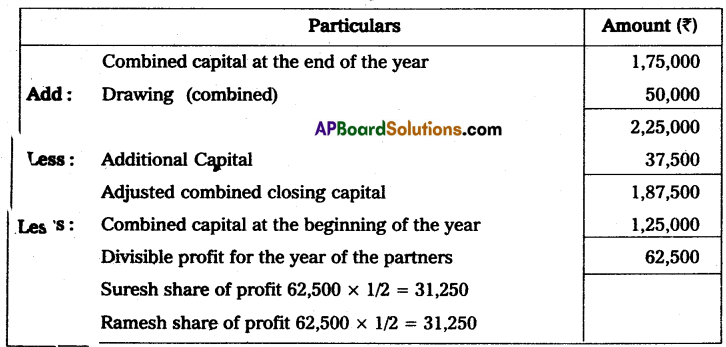
Suresh and Ramesh are equal partners in a business in which the books of accounts are kept by a single-entry system. Their combined capital stood at the beginning of the year at ₹ 1,25,000 and the combined capital at the end of the year stood at ₹ 1,75,000. During the year they have withdrawn ₹ 50,000 equally for their personal use and introduced ₹ 37,500 as fresh capital. Compute the profit for the year by preparing a statement of profit.
Solution:
Statement showing Profit or Loss
![]()
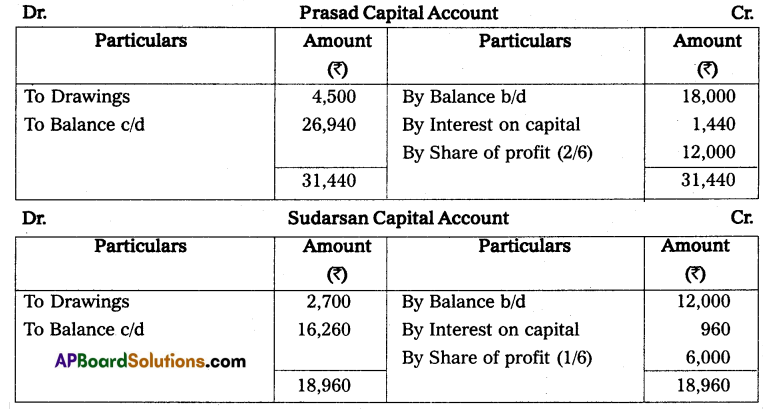
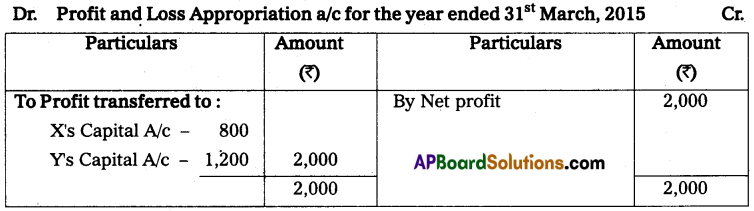
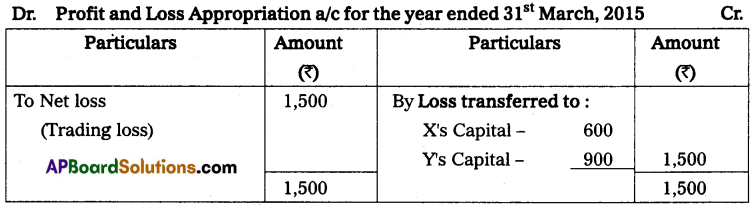
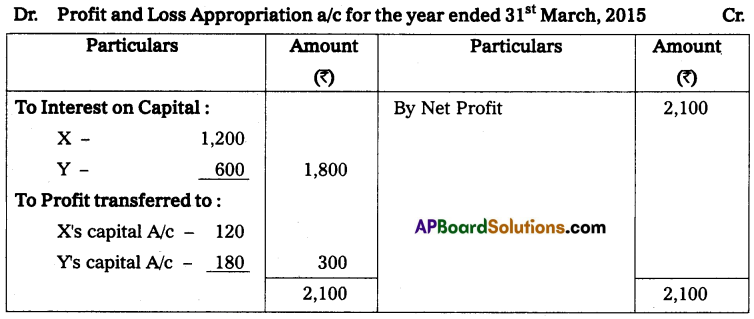
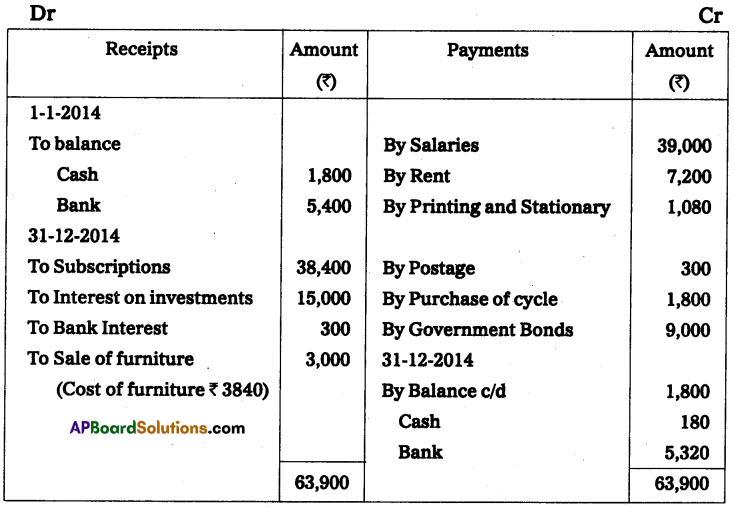
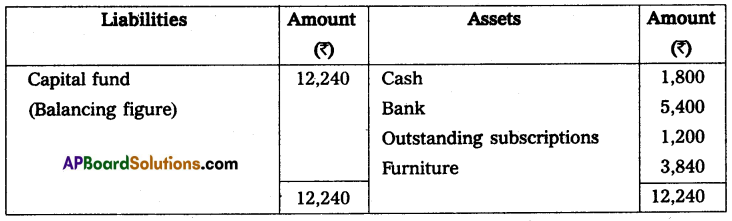
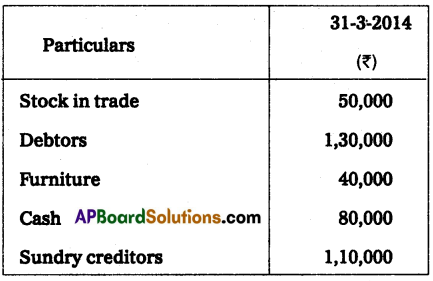
Question 11.
X and Y are partners sharing profits and losses in the ratio of 3 : 2 who keep their books on a single entry system on 1st April 2013. Their capital accounts show a balance of ₹ 60,000 and 70,000 respectively. During the year they have withdrawn ₹ 2,000 and ₹ 3,000 for their personal use. Find out the capitals at the end of the year. Also, calculate the divisible profit for the year ending 31-03-2014.
Solution:
Statement of affairs as on 31-03-2014
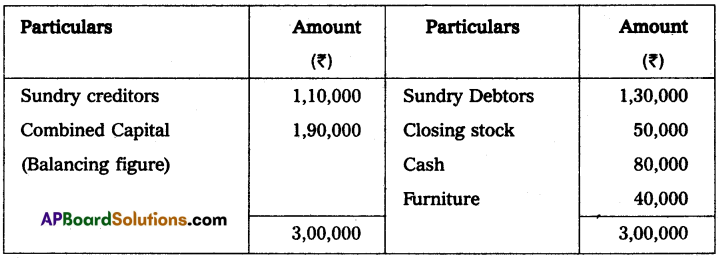
Statement of Profit or Loss as on 31-03-2014