AP Inter 2nd Year Maths 2B Important Questions Chapter 8 అవకలన సమీకరణాలు

Students get through AP Inter 2nd Year Maths 2B Important Questions Chapter 8 అవకలన సమీకరణాలు which are most likely to be asked in the exam.

AP Inter 2nd Year Maths 2B Important Questions Chapter 8 అవకలన సమీకరణాలు

ప్రశ్న 1.
అవకలన సమీకరణం \(\frac{d^2 y}{d x^2}=-p^2 y\) పరిమాణం తరగతి కనుక్కోండి.
సాధన:
దత్త సమీంకరణం \(\frac{d^2 y}{d x^2}\) బహపద లో తరగతి \(\frac{d^2 y}{d x^2}\) గరిష్ట పరిమాణము 2 పరిమాణువు.

ప్రశ్న 2.
\(\left(\frac{d^3 y}{d x^3}\right)^2-3\left(\frac{d y}{d x}\right)^2-e^x=4\) పరిమాణా, తరగతి కనుక్కోంది?
సాధన:
\(\frac{\mathrm{dy}}{\mathrm{dx}}\) మరియు \(\frac{d^3 y}{d x^2}\) లలో ఐహుపది సమీకరణ
\(\frac{\mathrm{d}^3 \mathrm{y}}{\mathrm{dx}^3}\) మొక్క ఘాతము. తరగత 2.
\(\frac{\mathrm{d}^3 \mathrm{y}}{\mathrm{dx}^3}\) గరిష్ట పరిమాణము అవకలనము సమీకరణ పరిమాణం 3.

ప్రశ్న 3.
\(x^{\frac{1}{2}}\left(\frac{d^2 y}{d x^2}\right)^{\frac{1}{3}}+x \frac{d y}{d x}+y=0\) పరిమాణం 2 తరగతి 1 అని చూపండి.
సాధన:

ప్రశ్న 4.
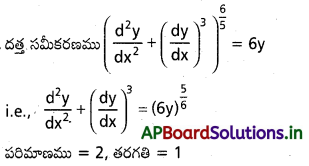
\(\left(\frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^3\right)^{\frac{6}{5}}=6y\) పరిమాణం, తరగతి కనుక్కోండి.
సాధన:

ప్రశ్న 5.
c యావ్చ్చిక స్థిర సంఖ్య యయతే y=c(x-c)² అనుగుణముగా ఉన్న అవకలన సమీకరణం పరిమాణము కనుక్కోండి.
సాధన:
y=c(x-c)² దత్త అవకలన సమీకరణము
\(\frac{d y}{d x}=2 c(x-c)\)
∴ అకలన సమీకరణ తరగతి

ప్రశ్న 6.
A, B, C ల యాదృచ్ఛిక స్థిర సంఖ్యలు అయితే y=Ae^x+Be^3x+Ce^5x  అనుగుణంగా గల అవకలన సమీకరణ పరిమాణం కనుక్కోండి.
సాధన:
\(y, \frac{d y}{d x}, \frac{d^2 y}{d x^2},\frac{d^3 y}{d x^3}\) ల నుండి A,B,C లసు తొలగిస్తే దత్త సమీకరణములు
గరిష్ఠ తరగతి \(=\frac{d^3 y}{d x^3}\)
అవకలన సమీకరణ పరిమాణము = 3

ప్రశ్న 7.
ఒక యాదృచ్ఛిక స్థిర సంఖ్య అయితే  y = cx – 2c² , అనుగుణముగా వచ్చే అవకలన సమీకరణం కనుక్కోండి.
సాధన.
y = cx – 2c² ………………….. (1)
x దృష్ట్రా అవకలనం చేయగా
\(\frac{d y}{d x}=c\)
(1) లో ప్రతిక్షేపిస్తే కావలసిన అవకలన సమీకరణము
\(y=x \cdot\left(\frac{d y}{d x}\right)-2\left(\frac{d y}{d x}\right)^2\)

ప్రశ్న 8.
A, B లు యాదృచ్ఛిక స్థిరసంఖ్య అయితే y =A cos 3 x+B sin 3 x  అనుగుణంగా ఉన్న అవకలన సమీకరణాన్ని ఏర్పరచండి.
సాధన:
y=A cos 3 x+B sin 3 x అని ఇవ్వబడింది.
x దృష్ట్రా అవకలనం చేయగా
\(\frac{d y}{d x}\) = – 3A sin 3x + 3B cos 3x
x దృష్టాల అవకలనం చేయగా
\(\frac{d^2 y}{d x^2}\)  =-9 A cos 3 x-9 B sin 3 x
=-9(A cos 3 x+B sin 3 x)
=-9 y
\(\frac{d^2 y}{d x^2}\) +9y=0

ప్రశ్న 9.
a, b లు యాదృచ్ఛిక స్థిర సంఖ్యలు అయితే r వ్యాసార్ధం గల వృత్తాలకు కటలంబం (x – a²) + (y – b)² = r² అనుగుణంగా ఉన్న అవకలన సమీకరణాన్ని ఏర్పరచండి.
సాధన:

ప్రశ్న 10.
మాల బిందువు గుండా ఏోతూ కేంద్రాలు Y- ఇక్షంపై మీద గల వృత్తాల కుటుంబానికి అనుగుణంగా అవకలన సమీకరణాన్ని రాబట్టండి.
సాధన:
మూల బిందువు గుండా టోవు Y-అక్షము మీద కావలసిన సమీకరణం.
x²+y²+2hy=0
h పరిమాణం
x దృష్ట్లా అవకలనం చేయగా

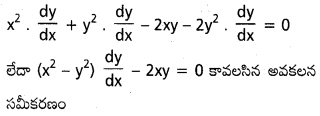
ప్రశ్న 11.
కింది అవకలన సమీకరణాలను f(x) d x+g(y) d y=0 రూపంలో ఏ్రాయండి

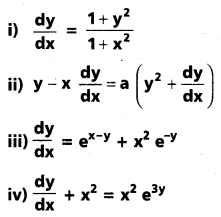
సాధన:
(i)

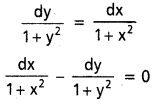
(ii) \(y-x \frac{d y}{d x}=a\left(y^2+\frac{d y}{d x}\right)\)
సాధన:

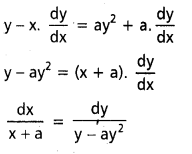
(iii) \(\frac{d y}{d x}=e^{x-y}+x^2 e^{-y}\)
సాధన:

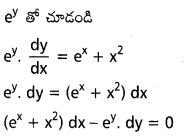
(iv) \(\frac{d y}{d x}+x^2=x^2 \cdot e^{3 y}\)
సాధన:

ప్రశ్న 12.
\(x+y \frac{dy}{dx}=0\) సాధారణ సాధన కనుక్కోండి.
సాధన:
దత్త సమీకరణం \(x+y \cdot \frac{dy}{dx}\) =0
x d x+y cdot d y=0
సమీకరణము చేయగా
\(\frac{x^2}{2}+\frac{y^2}{2}=c\) లేదా x²+y²=2c=c’

ప్రశ్న13.
\(\frac{d y}{d x}=e^{x+y}\) సాధారణ సాధన కనుక్కోండి.
సాధన:

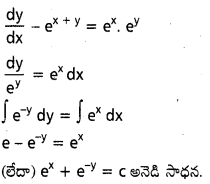
ప్రశ్న 14.
\(y^2-x \frac{d y}{d x}=a\left(y+\frac{d y}{d x}\right)\)
సాధన:

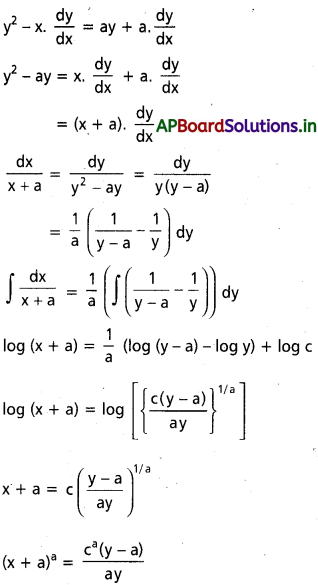
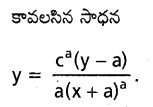
ప్రశ్న 15.
\(\frac{d y}{d x}=\frac{y^2+2 y}{x-1}\) ను సాధించండి.
సాధన:

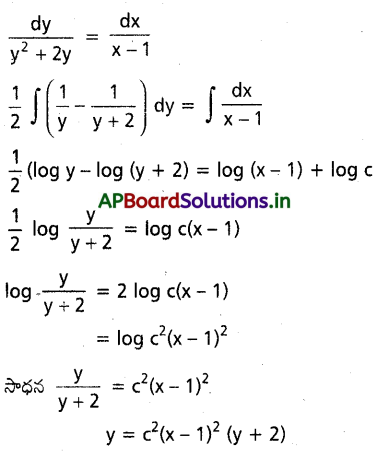
ప్రశ్న 16.
\(\frac{d y}{d x}=\frac{x(2 \log x+1)}{\sin y+\cos y}\) సాధించండి.
సాధన:
దత్త సమీకరణాలు
(sin y +  y cos y)dy = x(2 logx + 1) dx రాయవచ్చును.
∫ sin y dy + ∫ y cos y dy
=∫ 2x log x dx +∫ x dx
∫ sin y dy + y sin y – ∫ sin y dy
= x² log x – ∫ x².\(\frac{1}{\bar{x}}\)dx + ∫ x dx + c
y sin y = x² log x + c

ప్రశ్న 17.
x=3 అయినప్పుడు y=1 అవుతూ, 3 బిందువు (x, y) వద్దనైనా వాలు \(\frac{y}{x^2}\pi\) ఉన్న వక్రం సమీకరణాన్ని కనుక్రోండి.
సాధన:
ఏ బిందువు = \(\frac{dy}{dx}\)
అని ఇవ్వబడింది \(\frac{d y}{d x}=\frac{y}{x^2}\)

ప్రశ్న 18.
y(1+x) d x+x(1+y) d y=0 ను సాధించండి.
సాధన:

ప్రశ్న 19.
\(\frac{d y}{dx}\) = sin (x+y)+cos (x+y) ను సాధించండి.
సాధన:

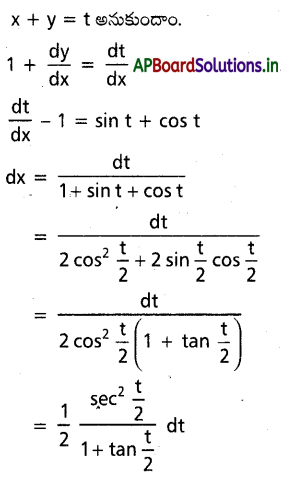
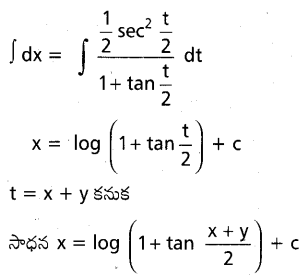
ప్రశ్న 20.
\((x-y)^2 \cdot \frac{d y}{d x}=a^2\) ను సాధించండి.
సాధన:

ప్రశ్న 21.
\(\sqrt{1+x^2} \sqrt{1+y^2}\) dx+xy d y=0  ను సాధించండి.
సాధన:

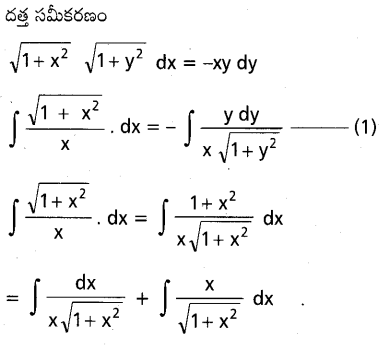
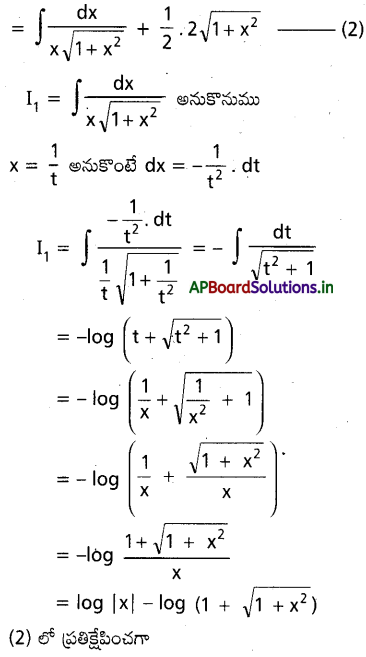
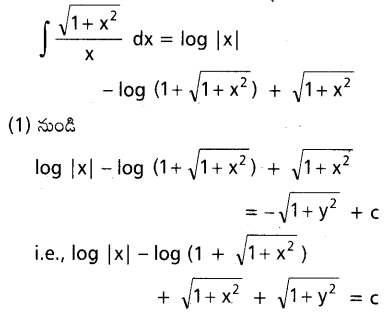
ప్రశ్న 22.
\(\frac{d y}{dx}=\frac{x-2 y+1}{2 x-4 y}\) ను సాధించండి.
సాధన:

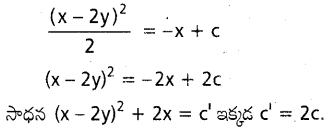
ప్రశ్న 23.
\(\frac{d y}{d x}=\sqrt{y-x}\) ను సాధించండి.
సాధన:

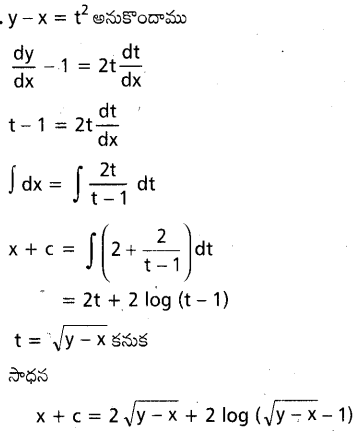
ప్రశ్న 24.
\(\frac{d y}{d x}+1=e^{x+y}\) ను సాధించండి.
సాధన:

ప్రశ్న 25.
\(\frac{dy}{dx}\) = (3 x+y+4)² ను సాధించండి.
సాధన:

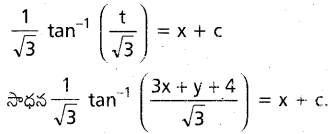
ప్రశ్న 26.
\(\frac{dy}{dx}\) -x tan (y-x)=1 ను సాధించండి.
సాధన:

ప్రశ్న 27.
f(x, y)=1+e^x/y ప్రమేయం x, y లలో సమఘాతం పమేయం అనిచూపండి.
సాధన:
f(k x, x y)=1+e^kx/ky = 1+e^x/y =f(x, y) f(x, y) తరగతి =0.

ప్రశ్న 28.
f(x, y) =x \(\sqrt{x^2+y^2}-y^2\) ప్రమేయం x, y లలో సమఘాతీయ ప్రమేయం అని చూపండి.
సాధన:

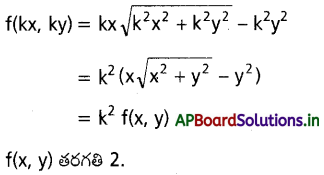
ప్రశ్న 29.
f(x, y)=x-y log y+y log x ప్రమేయం x,y లలో సమఘాతీయ ప్రమేయం అని చూపండి.
సాధన:
f(kx, ky) = kx – ky. log ky + ky log (kx)
= k(x- y log (ky) + y log kx)
= k(x – y log k – y log y + y log k + ylogx)
= k[x  –  y log y + y log x]
=k.f (xy)
f(x, y) తరగతి 1.

ప్రశ్న 30.
\(\left(1+e^{x / y}\right) d x+e^{x / y}\left(1-\frac{x}{y}\right) dy=0\) ను \(\frac{d x}{d y}=F\left(\frac{x}{y}\right)\) రూపంలో రాయండి.
సాధన:

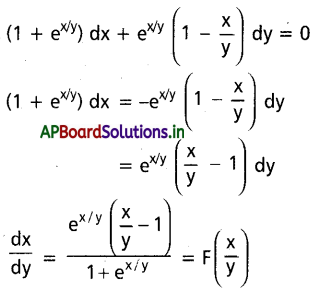
ప్రశ్న 31.
\(\left(x \sqrt{x^2+y^2}-y^2\right)\) dx + xy dy = 0 \(\frac{d y}{d x}=F\left(\frac{y}{x}\right)\) రూపంలో రాయండి.
సాధన:

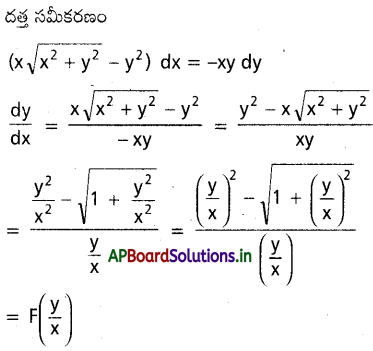
ప్రశ్న 32.
\(\left(x \sqrt{x^2+y^2}-y^2\right)\) dx + xy dy = 0 \(\frac{d y}{d x}=F\left(\frac{y}{x}\right)\) రూపంలో రాయండి.
సాధన:

ప్రశ్న 33.
\(\frac{d y}{d x}=\frac{y^2-2 x y}{x^2-x y}\) ను సాధించండి.
సాధన:

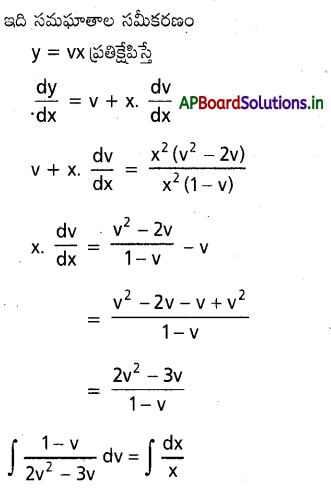
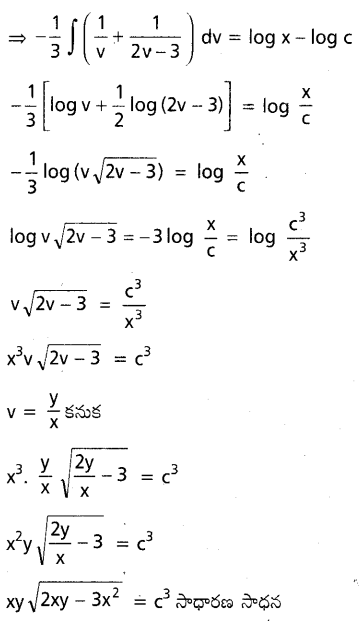
ప్రశ్న 34.
(x²+y²) d x=2xy dy ను సాధించండి.
సాధన:
దత్త సమీకరణాన్ని
\(\frac{d y}{d x}=\frac{x^2+y^2}{2xy}\) గా రాయగలరు

ప్రశ్న 35.
xy²dy – (x³ +y³)dx = 0 సాధించండి.
సాధన:

ప్రశ్న 36.
\(\frac{d y}{d x}=\frac{x^2+y^2}{2 x^2}\) …….. 1 సాధించండి.
సాధన:

ప్రశ్న 37.
x sec \(\left(\frac{\mathbf{y}}{\mathbf{x}}\right)\) (dx+x dy) =y cosec \(\left(\frac{\mathbf{y}}{\mathbf{x}}\right)\) ((x dy – y dx)
సాధన:

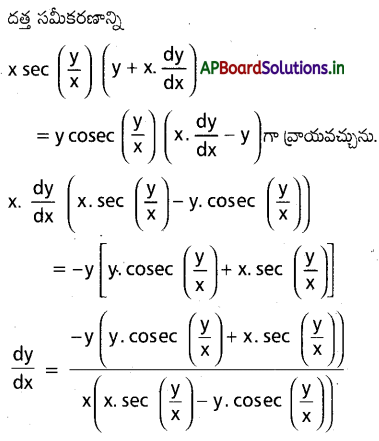
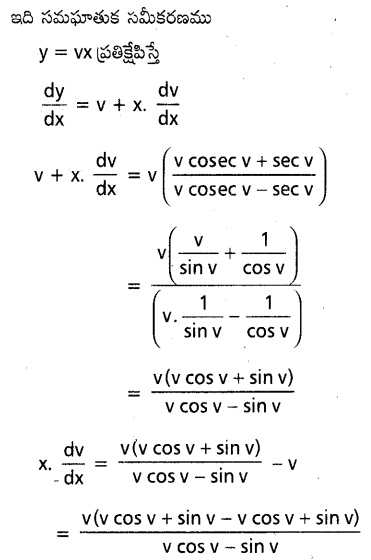
ప్రశ్న 38.
\(\left(1, \frac{\pi}{4}\right)\) బిందువు గుండా హోయే  x sin² \(\frac{y}{x}\) dx = y dx – xdy అవకలన సమీంకరణ సాధనను కనుక్కోండి.
సాధన.
దత్త సమీకరణాన్ని
\(\left(x \sin ^2 \frac{y}{x}-y\right) d x=-x dy\)

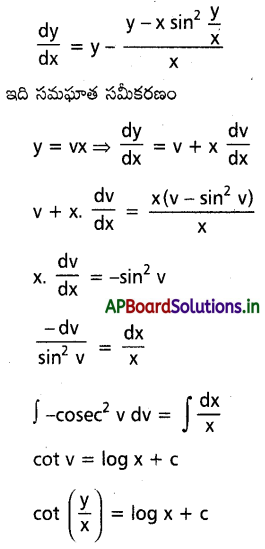
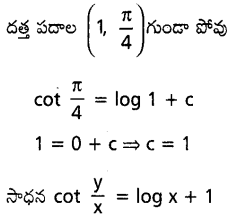
ప్రశ్న 39.
(x³ – 3xy²) dx + (3x²y – y³) dy = 0
సాధన:

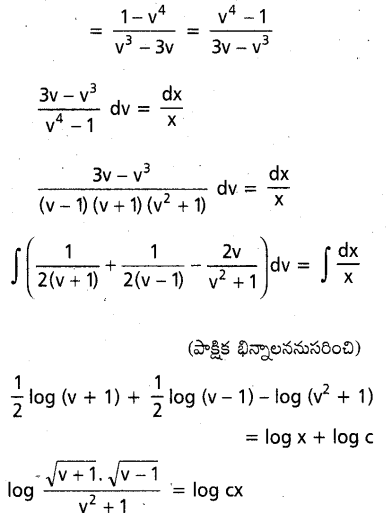
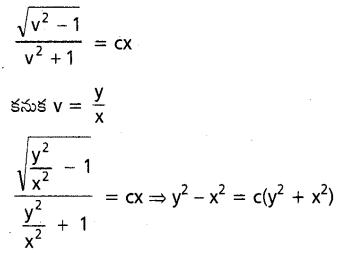
ప్రశ్న 40.
క్రింది అవకలన సమీకరణాలలో ప్రథమ పరిమాణం ఏకఘాత సమీకరణాల రూపంలో రాయండి.
x log x \(\frac{dy}{dx}\) +y=2 log x
సాధన:

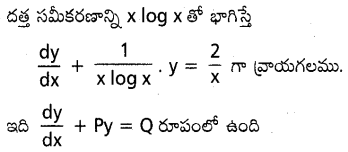
ప్రశ్న 41.
\(\left(x+2 y^3\right) \frac{dy}{dx}=y\)
సాధన:

ప్రశ్న 42.
క్రింద రెండో అవకలన సమీకరణాలను ఏకఘాతం సమీకరణ రూపంలో (I.F) కనుక్కోండి.
(cos x) \(\frac{\mathbf{d y}}{\mathbf{d x}}\) +y sin x =tanx.
సాధన:

ప్రశ్న 43.
\(\left(2 x-10 y^3\right) \frac{d y}{d x}+y=0\)
సాధన:

ప్రశ్న 44.
\(\left(1+x^2\right) \frac{d y}{d x}+2 x y-4 x^2=0\) ను సాధించండి.
సాధన:

ప్రశ్న 45.
\(\frac{1}{x} \frac{d y}{d x}+y e^x=e^{(1-x) e^x}\)
సాధన:
దత్త సమీకరణాన్ని
\(\frac{d y}{d x}+\left(x . e^x\right) \cdot y=x \cdot e^{(1-x) e^x} \pi\) గా వ్రాయవచ్చును.

ప్రశ్న 46.
sin² x \(\frac{dy}{dx}+y=cotx \) ను సాధించండి.
సాధన:

ప్రశ్న 47.
x=3 అయినపుడు y=9 అహ్యే \(x(x-2) \frac{d y}{d x}-2(x-1) y=x^3(x-2)\) అనే అవకలన సమీకరణం ప్రత్యేక సాధనము కనుక్టోండి.
సాధన:
దత్త సమీకరణము

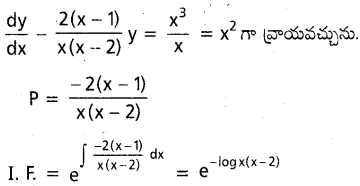
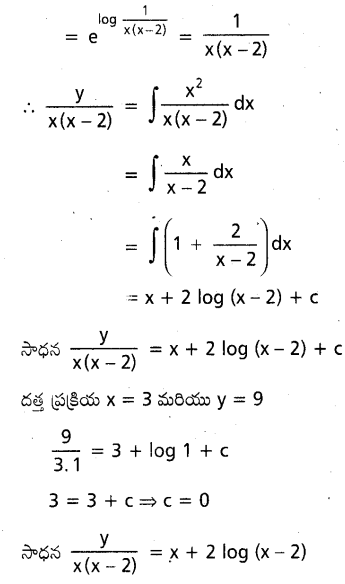
ప్రశ్న 48.
(1 +y²)dx=(tan^-1y – x)dy ను సాధించండి.
సాధన: