AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Ex 6(f)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 6 సమాకలనం Exercise 6(f) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 6 సమాకలనం Exercise 6(f)

అభ్యాసం – 6(ఎఫ్)

I. కింది సమాకలనులను గణించండి.

ప్రశ్న 1.
∫e^x (1 + x²) dx
సాధన:
∫e^x (1 + x²) dx = ∫e^x dx + ∫x² . e^x dx
= e^x + (x² . e^x – 2 ∫x. e^x dx)
= e^x + x² . e^x – 2x. e^x + 2e^x + C
= e^x(x² – 2x + 3) + C

ప్రశ్న 2.
∫x² e^-3x dx
సాధన:
∫x² e^-3x dx = \(\frac{x^2 \cdot e^{-3 x}}{-3}\) + \(\frac{1}{3}\)∫e^-3x. 2x dx
= –\(\frac{x^2 \cdot e^{-3 x}}{3}\) + \(\frac{2}{3}\)(\(\frac{x \cdot e^{-3 x}}{-3}\) + \(\frac{1}{3}\)∫e^-3xdx)
= \(\frac{-x^2 \cdot e^{-3 x}}{3}\) – \(\frac{2}{9}\)x. e^-3x – \(\frac{2}{27}\)e^-3x + C
= \(\frac{-\mathrm{e}^{-3 x}}{27}\)(9x² + 6x + 2) + C

ప్రశ్న 3.
∫x³ e^ax dx
సాధన:

II.

ప్రశ్న 1.
n ధన పూర్ణాంకం అయితే
∫xⁿ e^-x dx = -xⁿe^-x + n∫x^{n – 1}e^-x dx
అని చూపండి.
సాధన:
∫xⁿ e^-x dx = -xⁿe^-x + n∫x^{n – 1}e^-x dx
= -xⁿ. e^-x + n∫x^{n – 1}e^-x dx

ప్రశ్న 2.
పూర్ణాంకము n ≥ 2, 1 = | cosⁿ x dx, అయితే I_n = \(\frac{1}{n}\) cos^n-1 x sin x + \(\frac{n-1}{n}\) అని చూపండి.
సాధన:
I_n = ∫cosⁿ x dx = ∫cos^{n – 1}. cos x dx
= cos^{n – 1}x. sin x – ∫ sin x. (n – 1) cos^{n – 2}(-sin x) dx
= cos^{n – 1}x. sin x + (n – 1)I_{n – 2} – (n – 1)I_n
∴ I_n(1 + n – 1) = cos^{n – 1}x. sin x + (n – 1)I_{n – 2}
I_n = \(\frac{\cos ^{n-1} x \sin x}{n}\) + \(\frac{n-1}{n}\)I_n-2

III.

ప్రశ్న 1.
ధన పూర్ణాంకము n ≥ 2, I<sub.n = ∫ cotⁿ x dx, కు లఘూకరణ సూత్రాన్ని రాబట్టండి. దాని నుంచి ∫cot⁴ x dx విలువ రాబట్టండి. (A.P. Mar. ’16 (May ’11))
సాధన:
I_n = ∫ cotⁿ x dx = ∫ cot^{n – 2}x. cot² x dx
= ∫cot^n-2x. (cosec²x – 1) dx
= ∫cot^n-2x. cosec² x dx – I_{n – 2}
= –\(\frac{\cot ^{n-1} x}{n-1}\) – I_{n – 2}
n = 4 ⇒ I₄ = –\(\frac{\cot ^3 x}{3}\) – I₂
n = 2 ⇒ I₂ = -cot x – I,sub>0 ఇక్కడ I₀ = ∫dx = x
I₂ = -cot x – x
I₄ = \(-\frac{\cot ^3 x}{3}\) – (-cot x – x) + C
= \(-\frac{\cot ^3 x}{3}\) + cot x + x + C

ప్రశ్న 2.
ధన పూర్ణాంకము n ≥ 2, I_n = ∫ cosecⁿ x dx కు లఘుకరణ సూత్రాన్ని రాబట్టండి. దాని నుంచి ∫ cosec x dx విలువ రాబట్టండి.
(T.S. Mar. ’16)
సాధన:

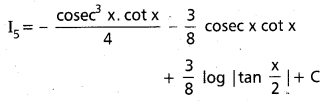
ప్రశ్న 3.
n ధనపూర్ణాంకం, పూర్ణాంకం m ≥ 2, I_m,n = ∫sin^mx cosⁿ x dx అయితే
I_m,n = –\(\frac{\sin ^{m-1} x \cos ^{n+1} x}{m+n}\) + \(\frac{m-1}{m+n}\)I_{m-2, n} అని చూపండి.
సాధన:

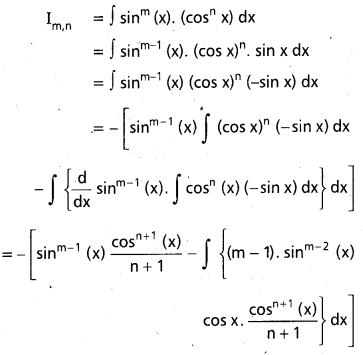
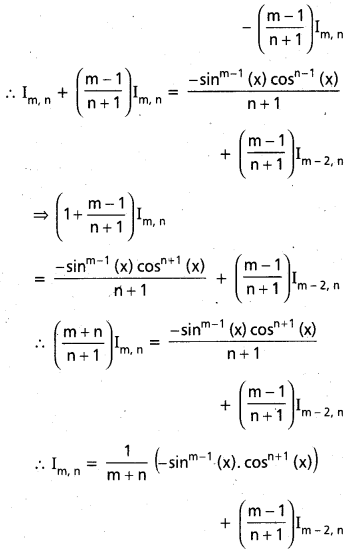
ప్రశ్న 4.
∫ sin⁵ cos⁴ dx గణించండి.
సాధన:
లఘుకరణ సూత్రం

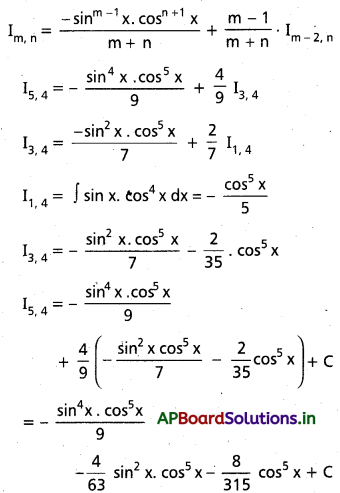
ప్రశ్న 5.
I_n = ∫(log x)ⁿdx, అయితే I_n = x (log x)ⁿ – n. I_n-1, అని చూపి, దాని నుంచి ∫(log x)⁴ dx ను కనుక్కోండి.
సాధన:
సాధన:
I_n = ∫(log x)ⁿ dx
= (log x)_n. x – ∫x . n . (log x)^{n – 1}. \(\frac{1}{x}\) dx
= x. (log x)ⁿ – n ∫ (log x)<supn – 1 dx
= x (log x)ⁿ – n. I_n-1
I₄ = x(log x)⁴ – 4. I₃
I₃ = (x log x)³ – 3. I₂
I₂ = (x log x)² – 2. I₁
I₁ = x log x – x
I₂ = (x(log x)² – 2x log x + 2x
(x (log x)³ – 3(x (log x)² – 2x log x + 2x)
= x. (log x)³ – 3x (log x)² + 6x (log x) – 6x
I₄ = x(log x)⁴ – 4[x. (log x)³ – 3x (log x)² + 6x (log x) – 6x] + C
= x(log x)⁴ – 4(log x)³ + 12(log x)² – 24 (log x) + 24] + C