AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Ex 8(d)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(d) will help students to clear their doubts quickly.

AP Inter 2nd Year Maths 2B Solutions Chapter 8 అవకలన సమీకరణాలు Exercise 8(d)

అభ్యాసం – 8(డి)

I. క్రింది అవకలన సమీకరణములను సాధించండి.

ప్రశ్న 1.
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(-\frac{(12 x+5 y-9)}{5 x+2 y-4}\)
సాధన:
b = -5, a = 5 ⇒ b = -a
(5x + 2y – 4)dy = (12x + 5y – 9) dx
(5x + 2y – 4)dy + (12x + 5y – 9) dx = 0
5 (x dy + y dx) + 2y dy – 4 dy + 12 x dx – 9 dx = 0
సమాకలనముచేయగా 5xy + y² – 4y + 6x² – 9x = c

ప్రశ్న 2.
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(\frac{-3 x-2 y+5}{2 x+3 y+5}\)
సాధన:
b = -2, a = 2 ⇒ b = -a
(2x + 3y + 5) dy = (- 3x – 2y + 5) dx
2x dy + 3y dy + 5 dy = -3x dx – 2y dx + 5 dx
2(x dy + y dx) + 3y dy + 3x dx + 5 dy – 5 dx = 0
సమాకలనము చేయగా
2xy + \(\frac{3}{2} y^2\) + \(\frac{3}{2} x^2\) + 5y – 5x = c
4xy + 3y² + 3x² – 10x + 10y = 2c = c’
సాధన
4xy + 3(x² + y²) – 10(x – y) = c

ప్రశ్న 3.
\(\frac{d y}{d x}\) = \(\frac{-3 x-2 y+5}{2 x+3 y-5}\)
సాధన:
\(\frac{d y}{d x}\) = \(\frac{-(3 x-2 y+5)}{2 x+3 y-5}\)
ఇక్కడ b = -2, a’ = 2
∵ b = -a’
(2x + 3y – 5) dy = -(3x – 2y + 5) dx
⇒2(x dy + y dx) + (3y – 5) dy + (3x – 5) dx = 0
⇒ 2d (xy) + (3y – 5) dy + (3x – 5) dx = 0
ఒక్కొక్కదాన్ని సమాకలనము చేయగా
2 \(\int\)d (xy) + \(\int\) (3y – 5) dy + \(\int\) (3x – 5) dx = 0
⇒2xy + 3.\(\frac{y^2}{2}\) – 5y + 3\(\frac{x^2}{2}\) – 5x = \(\frac{c}{2}\)
(లేదా) 3x² + 4xy + 3y² – 10x – 10y = c
కావలసిన సాధన

ప్రశ్న 4.
2(x – 3y + 1) \(\frac{d y}{d x}\) = 4x – 2y + 1
సాధన:
(2x – 6y + 2) dy = (4x – 2y + 1) dx
(2x – 6y + 2) dy – (4x – 2y + 1) dx = 0
2 (x dy + y dx) – 6y dy + 2 dy – 4x dx – dx = 0
సమాకలనము చేయగా, సాధన
2xy – 3y² – 2x² + 2y – x = c

ప్రశ్న 5.
\(\frac{d y}{d x}\) = \(\frac{x-y+2}{x+y-1}\)
సాధన:
b = -1, a’ – 1 ⇒ b = – a’
(x + y – 1) dy = (x – y + 2) dx
(x + y – 1) dy = (x − y + 2) dx = 0
(x dy + y dx) + y dy – dy – x dx – 2 dx = 0
సమాకలనము చేయగా
xy + \(\frac{y^2}{2}\) – \(\frac{x^2}{2}\) – y – 2x = c
2xy + y² – x² – 2y – 4x = 2c = c’

ప్రశ్న 6.
\(\frac{d y}{d x}\) = \(\frac{2 x-y+1}{x+2 y-3}\)
సాధన:
b = -1, a’ = 1 ⇒ b = -a’
(x + 2y – 3) dy = (2x – y + 1) dx
(x + 2y – 3) dy – (2x – y + 1) dx = 0
(x dy + y dx) + 2y dy – 3 dy – 2x dx – dx = 0
సమాకలనము చేయగా
xy + y² – x² – 3y – x = c

II. కింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
(2x + 2y + 3) \(\frac{d y}{d x}\) = x + y + 1
సాధన:

9 తో గుణించగా
6v + log (3v + 4) = 9x + 9c
6(x + y) + log[3(x + y) + 4] = 9x + c
i.e. log (3x + 3y + 4) = 6y – 3x + c

ప్రశ్న 2.
\(\frac{d \mathbf{y}}{\mathbf{d x}}\) = \(\frac{4 x+6 y+5}{3 y+2 x+4}\)
సాధన:
\(\frac{d \mathbf{y}}{\mathbf{d x}}\) = \(\frac{4 x+6 y+5}{2 x+3 y+4}\)
v = 2x + 3y

64 తో గుణించగా
8v + 9 log (8v + 23) = 64x + 64c
8 (2x + 3y) – 64x + 9 log (16x + 24y + 23) = c’
8 తో భాగించగా
2x + 3y – 8x + \(\frac{9}{8}\) log (16x + 24y+23) = c”
3y – 6x + \(\frac{9}{8}\) log (16x + 24y + 23) = c”
3 తో భాగించగా సాధన
y – 2x + \(\frac{3}{8}\) log (16x + 24y + 23) = k

ప్రశ్న 3.
(2x + y + 1) dx + (4x + 2y – 1) dy = 0
సాధన:

2v + log (v – 1) = 3x + c
2v – 3x + log (v – 1) = c
2(2x + y) – 3x + log (2x + y – 1) = c
4x+2y-3x + log (2x + y – 1) = c
సాధన x + 2y + log (2x + y – 1) = c

ప్రశ్న 4.
\(\frac{d y}{d x}\) = \(\frac{2 y+x+1}{2 x+4 y+3}\)
సాధన:

8 తో గుణించగా
4v + log (4v + 5) = 8x + 8c
4(x + 2y) – 8x + log [4(x + 2y) + 5] = c’
సాధన
4x + 8y – 8x + log (4x + 8y + 5) = c’
8y – 4x + log (4x + 8y + 5) = c’

ప్రశ్న 5.
(x + y – 1) dy = (x + y + 1) dx
సాధన:

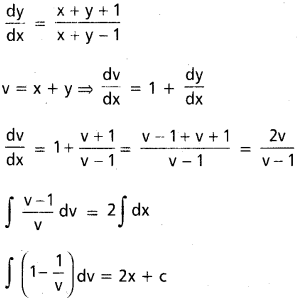
v – log v = 2x + c
x + y – log (x + y) = 2x – c
(x – y) + log (x + y) = c అనేది కావలసిన సాధన

III. కింది అవకలన సమీకరణాలను సాధించండి.

ప్రశ్న 1.
\(\frac{d y}{d x}\) = \(\frac{3 y-7 x+7}{3 x-7 y-3}\) (T.S. Mar. ’16)
సాధన:
x = x + h, y = y + k అనుకుంటే \(\frac{d y}{d x}\) = \(\frac{d y}{d x}\)


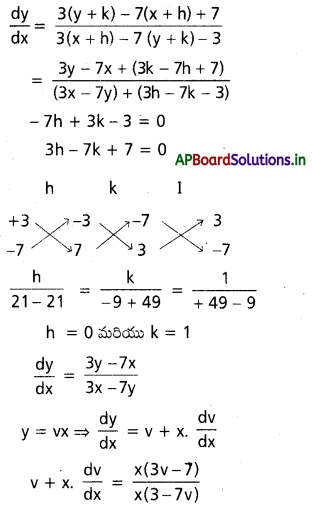
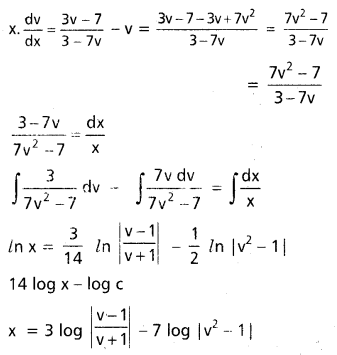
⇒ 14 ln x – ln c
= 3ln (v – 1) – 3ln (v + 1) – 7ln (v + 1) – 7ln (v – 1).
14ln x – ln c = 10 ln (v + 1) – 4 ln (v – 1)
ln (v + 1)⁵ + ln (v – 1)² + ln x⁷ = ln c
(v + 1)⁵. (v – 1)². x⁷ = c
\(\left(\frac{y}{x}+1\right)^5\left(\frac{y}{x}-1\right)^2\) . x⁷ = c
(y – x)² (y + x)⁵ = c
[y – (x – 1)]² (y + x – 1)⁵ = c
సాధన [y – x + 1]² (y + x – 1)⁵ = c.

ప్రశ్న 2.
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(\frac{6 x+5 y-7}{2 x+18 y-14}\)
సాధన:
\(\frac{\mathbf{d y}}{\mathbf{d x}}\) = \(\frac{6 x+5 y-7}{2 x+18 y-14}\)
x = X + h, y = Y + k


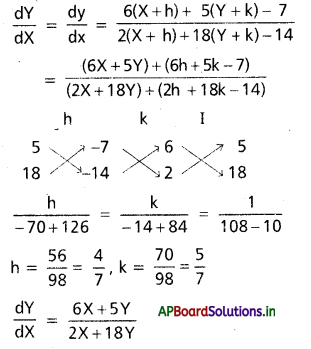
14 = A – \(\frac{7}{3}\) ⇒ A = 6
V = \(-\frac{1}{2}\) ⇒ 2 – 9 = B\(\left(-\frac{3}{2}-2\right)\)
-7 = \(-\frac{7}{2} B\) ⇒ B = 2
\(\int\left(\frac{6}{3 V-2}+\frac{2}{2 V+1}\right) d V\) = \(-3 \int \frac{d x}{x}\)
2 log(3V – 2) + log (2V + 1) = -3 log X + log c
log (3V – 2)².(2V + 1) + log X³ = log c
log X³(3V – 2) (2V + 1) = log c
X³(3v – 2)² (2V + 1) = c

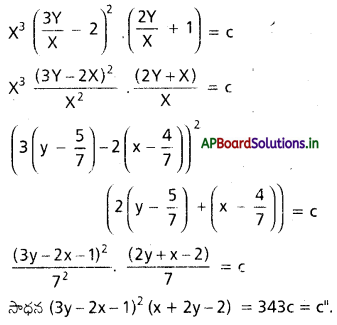
ప్రశ్న 3.
\(\frac{d y}{d x}\) + \(\frac{10 x+8 y-12}{7 x+5 y-9}\) = 0
సాధన:

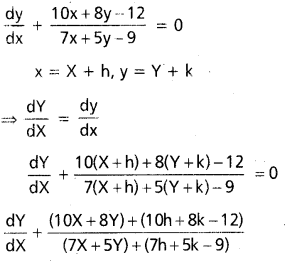
h, k విలువలను 10h + 8k – 12 = 0
7h + 5k – 9 = 0 అయ్యే విధంగా ఎన్నుకొందాం


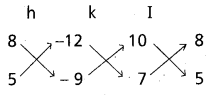
5V + 7 = A(V + 2) + B (V + 1)
V = -1 ⇒ 2 = A(-1 + 2) = A ⇒ A = 2
V = -2 = -3 = B(-2 + 1) = -B, B = 3
\(\int\left(\frac{2}{(V+1)}+\frac{3}{(V+2)}\right) d V\) = \(-5 \int \frac{d X}{X}\)
2 log(V + 1) + 3 log (V + 2) = -5 log x + c
c = 2log(V + 1) + 3 log(V + 2) + 5 log X
= log (V + 1)². (V + 2)³. X⁵
log \(\left(\frac{Y}{X}+1\right)^2\) . \(\left(\frac{Y}{X}+2\right)^3\). X⁵
= log \(\frac{(Y+X)^2}{X^2} \frac{(Y+2 X)^3}{X^3}\) . X⁵
⇒ (Y + X)² . (Y + 2X)³ = e^c = c¹
(Y + 1 – X – 2)² (Y + 1 – 2x – 4)³ = c
సాధన: (x + y – 1)² (2x + y – 3)³ = c.

ప్రశ్న 4.
(x – y – 2) dx + (x – 2y – 3) dy = 0
సాధన:
దత్త సమీకరణము \(\frac{d y}{d x}\) = \(\frac{-x+y+2}{x-2 y-3}\)
x = X + h, y = Y + k
\(\frac{d y}{d x}\) = \(\frac{-(X+h)+(Y+k)+2}{(X+h)-2(Y+k)-3}\)
= \(\frac{-X-h+(-h+2 k+2)}{(X-2 Y)+(h-2 k-3)}\)
h, k విలువలు – h + k − 2 = 0
h – 2k – 3 = 0 అయ్యేవిధంగా ఎన్నుకొందాం.




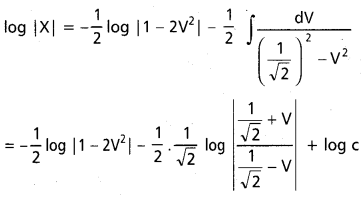
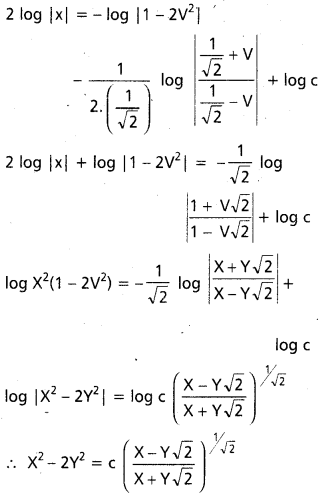
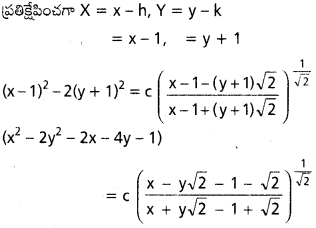
కావలసిన సాధన

ప్రశ్న 5.
(x – y) dy = (x + y + 1) dx
సాధన:
\(\frac{d y}{d x}\) = \(\frac{x+y+1}{x-y}\)
x = X +h, y = Y + k ⇒ \(\frac{d Y}{d X}\) = \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
\(\frac{d y}{d x}\) = \(\frac{X+h+Y+k+1}{(X+h)-(Y+k)}\)
= \(\frac{(X+Y)+(h+k+1)}{(X-Y)+(h-k)}\)
h, k విలువ లను h + k + 1 = 0
h – k = 0 అయ్యే విధంగా ఎన్నుకొందాం
సాధించగా h = \(-\frac{1}{2}\), k = \(-\frac{1}{2}\)
∴ \(\frac{d y}{d X}\) = \(\frac{X+Y}{X-Y}\)

tan^-1 V – \(\frac{1}{2}\)log (1 + v²) = log x + log c
2 tan^-1 V = log (1 + V²) + 2 log x + 2 log c = log c²x² (1 + v²)

ప్రశ్న 6.
(2x + 3y – 8) dx = (x + y – 3) dy
సాధన:
\(\frac{d y}{d x}\) = \(\frac{2 x+3 y-8}{x+y-3}\)
x = X + h, y = Y + k ⇒ \(\frac{\mathrm{d} Y}{\mathrm{~d} X}\) = \(\frac{\mathrm{dy}}{\mathrm{dx}}\)
\(\frac{d Y}{d X}\) = \(\frac{2(X+h)+3(Y+k)-8}{(X+h)+(Y+k)-3}\)
= \(\frac{(2 X+3 Y)+(2 h+3 k-8)}{(X+Y)+(h+k-3)}\)
h, k విలువ లను 2h + 3k – 8 = 0
h + k – 3 = 0 అయ్యే విధంగా ఎన్నుకొందాం


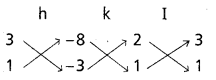
(1 + V) = A(2 – 2V) + B అనుకొందాం
V గుణకాలు సమానం చేయగా
1 = – 2A ⇒ A = -1/2
స్థిర పదాలు సమానం చేయగా
1 = 2A + B
= -1 + B
B = 2


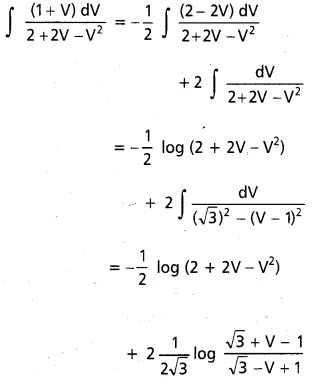
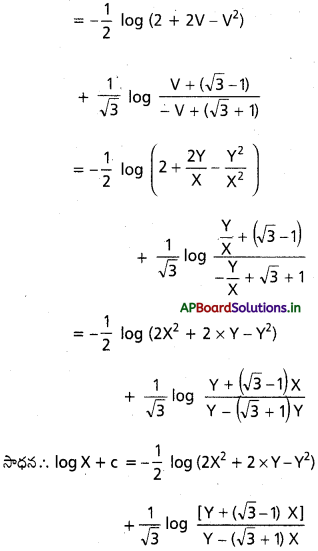
ఇక్కడ, X = x – 1, Y = y – 2

ప్రశ్న 7.
\(\frac{d y}{d x}\) = \(\frac{x+2 y+3}{2 x+3 y+4}\)
సాధన:
x = X + h, y = Y + k అయితే \(\frac{d \mathrm{Y}}{\mathrm{dX}}\) = \(\frac{d y}{d x}\)
\(\frac{d Y}{d X}\) = \(\frac{(X+h)+2(Y+k)+3}{2(X+h)+3(Y+k)+4}\)
= \(\frac{(X+2 Y)+(h+2 k+3)}{(2 X+3 Y)+(2 h+3 k+4)}\)
h, k విలువలకు h + 2k + 3 = 0
2h + 3k + 4 = 0 అయ్యే విధంగా ఎన్నుకొందాం.

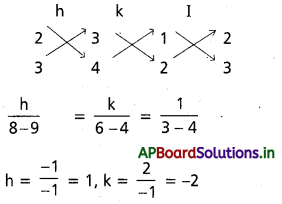
\(\frac{\mathrm{d} Y}{\mathrm{dX}}\) = \(\frac{X+2 Y}{2 X+3 Y}\)
ఇది సమఘాత సమీకరణము

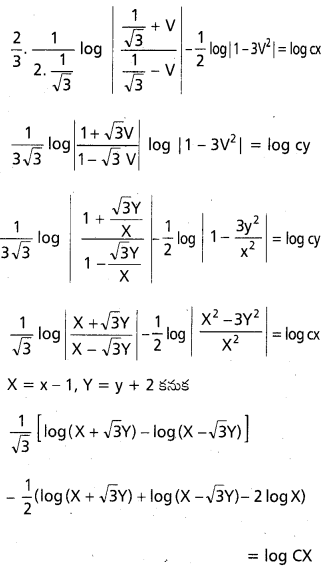
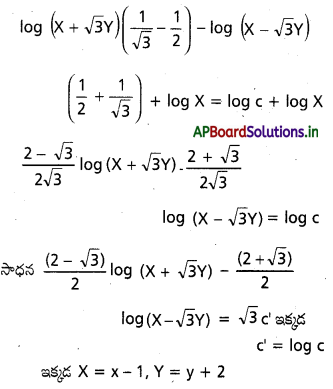
ప్రశ్న 8.
\(\frac{d y}{d x}\) = \(\frac{2 x+9 y-20}{6 x+2 y-10}\)
సాధన:
దత్త సమీకరణము \(\frac{d y}{d x}\) = \(\frac{2 x+9 y-20}{6 x+2 y-10}\)
x = X + h, y = Y + k ⇒ \(\frac{d Y}{d X}\) = \(\frac{d y}{d x}\)
\(\frac{\mathrm{dY}}{\mathrm{dX}}\) = \(\frac{2(X+h)+9(Y+k)-20}{6(X+h)+2(Y+k)-10}\)
= \(\frac{(2 X+9 Y)+(2 h+9 k-20)}{(6 X+2 Y)+(6 h+2 k-10)}\)
h, k విలువలను 2h + 6k – 20 = 0
6h + 2k – 10 = 0 అయ్యే విధంగా ఎన్నుకొందాం

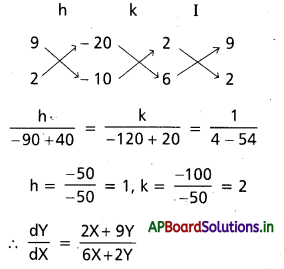
ఇది సమఘాత సమీకరణము
y = VX ⇒ \(\frac{d Y}{d X}\) = V + X. \(\frac{d V}{d X}\)


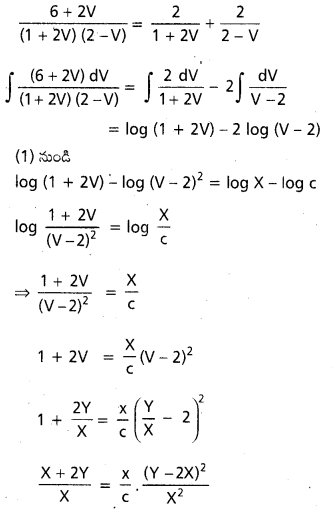
సాధన (X + 2Y) = (Y – 2X)²
ఇక్కడ X = x – 1, Y = y – 2
c(x – 1 + 2y – 4) = (y – 2 – 2x + 2)²
c(x + 2y – 5) = (y – 2x)²
= (2x – y)²