Students can go through AP SSC 10th Class Maths Notes Chapter 1 Real Numbers to understand and remember the concepts easily.
AP State Syllabus SSC 10th Class Maths Notes Chapter 1 Real Numbers
→ “God made the integers. All else is the work of man” …… Leopold Kronecker
→ Euclid’s division lemma: Given positive integers a, b there exists unique pair of integers q and r satisfying
a = bq + r; 0 ≤ r < b
This result was first published / recorded in book VII of Euclid’s “The Elements”.
→ Euclid’s division algorithm is a technique to compute the Highest Common Factor (H.C.F) of two given numbers.
E.g: HCF of 80 and 130
130 = 80 × 1 + 50 80 = 50 × 1 + 30
50 = 30 × 1 + 20 30 = 20 × 1 + 10
20 = 10 × 2 + 0 and H.C.F = 10
→ Euclid’s division algorithm can also be extended to all integers.
→ Numbers which can be expressed in the form p/q, where q ≠ 0 and ‘p and q’ are integers are called rational numbers; represented by Q.
Q = { \(\frac{p}{q}\) ; q ≠ 0; p, q ∈ Z} .
![]()
→ Every rational number can be expressed either as a terminating decimal or as a non-terminating recurring decimal.
→ Numbers which can’t be expressed in p/q form are called irrational numbers represented by S. You may notice that the first letter of surds is ‘S’.
Eg: √2, √3, √5, …….. etc,
→ The combined set of rationals and irrationals is called the set of Real numbers; represented by R.
R = Q ∪ S.
→ Diagramatic representation of the number system:
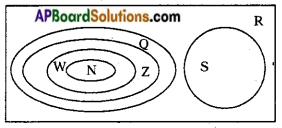
where N = the set of natural numbers; W = the set of whole numbers;
Z = the set of integers; Q = the set of rational numbers;
S = the set of irrational numbers ; R = the set of real numbers.
→ Fundamental Theorem of Arithmetic: Every composite number can be expressed as a product of primes uniquely, (i.e.,) if x is a composite number, then
x = \(p_{1}^{l} \cdot p_{2}^{m} \cdot p_{3}^{n}\) …… where p1, p2, p3, ….. are prime numbers and l, m, n, …… are natural numbers.
Eg: 420 = 2 × 210 = 2 × 2 × 105 = 2 × 2 × 3 × 35 = 2 × 2 × 3 × 5 × 7
i. e. 420 = 22 × 31 × 51 × 71 and the factorisation on the R.H.S is unique.
Note: R.H.S is called exponential form of 420.
→ To find the H.C.F. of two or more numbers:
Step (i): Express given numbers in their exponential form.
Step (ii): Take the common bases.
Step (iii): Assign the respective smallest exponent from their exponential forms.
Step (iv): Take the product of the above.
Eg: H.C.E of 60 and 75 is
Step (i) 60 = 22 × 3 × 5 ; 75 = 3 × 52
Step (ii) 3O × 5O [taking common bases]
Step (iii) 31 × 51 [∵ smallest exponent among 31 and 31 is 1]
Step (iv) 3 × 5 = 15 [smallest exponent among 51 and 52 is 1]
∴ H.C.F = 15
(i.e.) The highest common factor of the given set of numbers is the product of the com¬mon bases with the respective least exponents.
![]()
→ To find the L.C.M. of two or more numbers:
Step – 1: Express the given numbers in their exponential forms.
Step – 2: Take every base.
Step – 3: Assign the respective greatest exponent to each base.
Step – 4: Take the product of the above.
Eg: L.C.M. of 60 and 75 is
Step – 1: 60 = 22 × 3 × 5 ; 75 = 3 × 52
Step – 2: 2O × 3O × 5O
Step – 3: 22 × 31 × 52
Step – 4: 4 × 3 × 25 = 300
L.C.M = 300
→ We may notice that the product of any two numbers N1 and N2 is equal to the product of their L.C.M. (L) and H.C.F. (H).
i.e., N1 . N2 = L.H
→ Let x = p/q be a rational number. If the numerator p is divided by the denominator q, we get the decimal form of x. The decimal form of x may or may not be terminating, i.e., every rational number can be expressed either as a terminating decimal or a non-terminating decimal. This gives us the following theorems.
Theorem – 1: Let ‘x’ be a rational number when expressed in decimal form, terminates, then x can be expressed in the form p/q where p, q are co-primes and the prime factorization of q is of the form 2n × 5m, where n and m are non-negative integers.
Theorem – 2: Let x = p/q be a rational number, where q is of the form 2n × 5m then x has a decimal expansion that terminates.
Theorem – 3: Let x = p/q be a rational number, where p, q are co-primes and the prime factorization of q is not of the form 2n . 5m (n, m ∈ Z+) then x has a decimal expansion which is non-terminating recurring decimal.
Theorem – 4: Let ‘p’ be a prime number. If p divides a2 then p divides a, where ‘a’ is a positive integer.
→ If a is a non-zero rational number and b is any irrational number, then (a + b), (a – b), a/b and ab are all irrational numbers.
![]()
→ Properties of Real Numbers:
If a, b and c are any three real numbers we may notice that
- a + b is also a real number – closure property w.r.t. addition
a.b is also a real number – closure property w.r.t. multiplication - a + b = b + a – commutative property w.r.t. addition
a . b = b . a – commutative property w.r.t. multiplication - (a + b) + c = a + (b + c) – associative law w.r.t.
addition (a.b).c = a.(b.c) – associative law w.r.t. multiplication - a + 0 = 0 + a = a, where ‘0’ is the additive identity,
a × 1 = 1 × a = a, where 1 is the multiplicative identity, - a + (-a) = (-a) + a = 0 where (a) and (-a) are additive inverse of each other.
a × \(\frac{1}{a}\) = \(\frac{1}{a}\) × a = 1 where a and \(\frac{1}{a}\) are multiplicative inverse of each other.
→ If an = x, where a and x are positive integers and a ≠ 1, then we define logax = n read as logarithm of x to the base a is equal to n.
Eg.: 24 = 16 ⇒ log216 = 4
→ logax + logay = logaxy
→ logaa = 1
→ logax – logay = loga\(\frac{x}{y}\)
→ loga1 = 0
→ logaxm = m logax
→ In general, the bases in the logarithms are 10 (or) e, where e’ is approximated to 2.718.
→ If p is a prime number and p divides a2 then p divides ‘a’ also.