Students can go through AP SSC 10th Class Maths Notes Chapter 3 Polynomials to understand and remember the concepts easily.
AP State Syllabus SSC 10th Class Maths Notes Chapter 3 Polynomials
→ Polynomial: An algebraic expression in which the variables involved have only non-negative integer power is called a polynomial.
Ex: 2x + 5, 3x2 + 5x + 6, -5y, x3, etc.
→ Polynomials are constructed using constants and variables.
→ Coefficients operate on variables, which can be raised to various powers of non negative integer exponents.
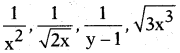 , etc. are not polynomials.
, etc. are not polynomials.
![]()
→ General form of a polynomial having nth degree is p(x) = a0xn + a1xn-1 + a2xn-2 …….. + an-1x + an where a0, a1, a2,…… an-1, an are real coefficients and a0 ≠ 0.
→ Degree of a polynomial:
The exponent of the highest degree term in a polynomial is known as its degree.
In other words, the highest power of x in a polynomial f(x) is called the degree of a polynomial f(x).
Example:
i) f(x) = 5x + \(\frac{1}{3}\) is a polynomial in the variable x of degree 1.
ii) g(y) = 3y2 – \(\frac{5}{2}\)y + 7 is a polynomial in the variable y of degree 2.
→ Zero polynomial: A polynomial of degree zero is called zero polynomial that are having only constants.
Ex: f(x) = 8, f(x) = –\(\frac{5}{2}\)
→ Linear polynomial: A polynomial of degree one is called linear polynomial.
Ex: f(x) = 3x + 5, g(y) = 7y – 1, p(z) = 5z – 3.
More generally, any linear polynomial in variable x with real coefficients is of the form f(x) = ax + b, where a and b are real numbers and a ≠ 0.
Note: A linear polynomial may be a monomial or a binomial because linear polynomial f(x) = \(\frac{7}{5}\)x – \(\frac{5}{2}\) is a binomial, whereas the linear polynomial g(x) = \(\frac{2}{5}\) x is a monomial.
→ Quadratic polynomial: A polynomial of degree two is called quadratic polynomial.
Ex: f(x) = 5x2, f(x) = 7x2 – 5x, f(x) = 8x2 + 6x + 5.
More generally, any quadratic polynomial in variable x with real coefficients is of the form f(x) = ax2 + bx + c, where a, b and c are real numbers and a ≠ 0.
Note: A quadratic polynomial may be a monomial or a binomial or a trinomial.
Ex: f(x) = \(\frac{1}{5}\)x2 is a monomial, g(x) = 3x2 – 5 is a binomial and
h(x) = 3x2 – 2x + 5 is a trinomial.
![]()
→ Cubic polynomial: A polynomial of degree three is called cubic polynomial.
Ex: f(x) = 8x3, f(x) = 9x3 + 5x2
f(y) = 11y3 – 9y2 + 7y,
f(z) = 13z3 – 12z2 + 11z + 5.
→ Polynomial of degree ‘n’ in standard form: A polynomial in one variable x of degree n is an expression of the form f(x) = anxn + an-1xn-1 + …….. + a1x + a0 where a0, a1, a2,…… an, an are constants and an ≠ 0.
In particular, if a0 = a1 = a2 = …… = an = 0 (all the constants are zero; we get the constants zero), we get the zero polynomial which is not defined.
→ Value of a polynomial at a given point: If p(x) is a polynomial in x and α is a real number. Then the value obtained by putting x = a in p(x) is called the value of p(x) at x = α.
Ex : Let p(x) = 5x2 – 4x + 2, then its value at x = 2 is given by
p(2) = 5(2)2 – 4(2) + 2 = 5(4) – 8 + 2 = 20 – 8 + 2 = 14 Thus, the value of p(x) at x = 2 is 14.
→ Graph of a polynomial: In algebraic or in set theory language, the graph of a polynomial f(x) is the collection (or set) of all points (x, y) where y = f(x).
i) Graph of a linear polynomial ax + b is a straight line.
ii) The graph of a quadratic polynomial (ax2 + bx + c) is U – shaped, called parabola.
→ If a > 0 in ax2 + bx + c, the shape of parabola is opening upwards ‘∪’.
![]()
→ If a < 0 in ax2 + bx + c, the shape of parabola is opening downwards ‘∩’
→ Relationship between the zeroes and the coefficient of a polynomial:
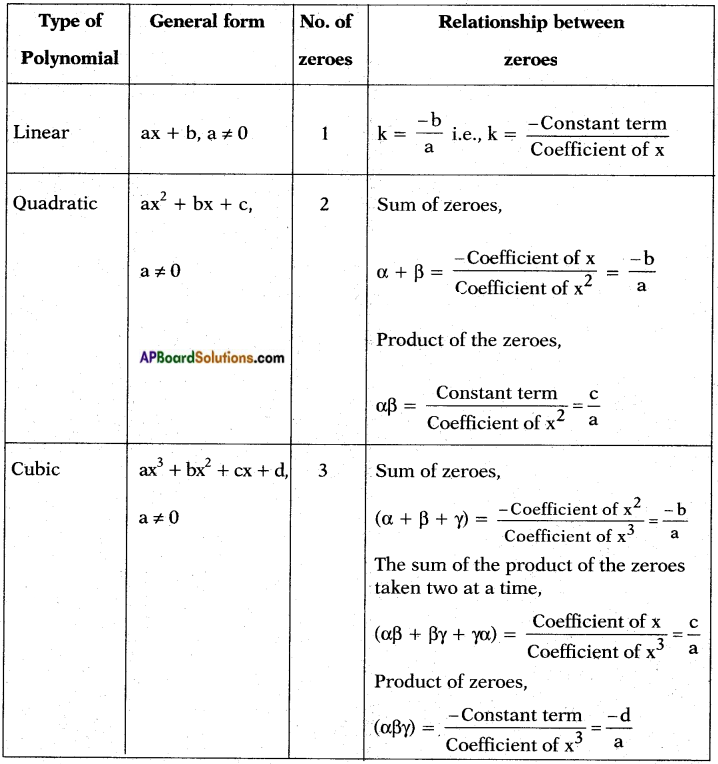
Note: Formation of a cubic polynomial : Let α, β, and γ be the zeroes of the polynomial.
∴ Required cubic polynomial = (x – α) (x – β) (x – γ).
→ How to make a quadratic polynomial with the given zeroes : Let the zeroes of a quadratic polynomial be α and β.
∴ x = α, x = β
Then, obviously the quadratic polynomial is (x – α) (x – β) i.e., x2 – (α + β)x 4- ap.
i.e., x2 – (sum of the zeroes) x + product of the zeroes.
→ Division Algorithm : If p(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x) such that, p(x) = g(x) × q(x) + r(x)
i.e., Dividend = Divisor × Quotient + Remainder
where, r(x) = 0 or degree of r(x) < degree of g(x). This result is known as the division algorithm for polynomials.
![]()
→ Some useful relations:
α2 + β2 = (α + β)2 – 2αp
(α – β)2 = (α + β)2 – 4αβ
α2 – β2 = (α + β) (α – β) = (α + β)\(\sqrt{(\alpha+\beta)^{2}-4 \alpha \beta}\)
α3 + β3 = (α + β)3 – 3αβ(α + β)
α3 – β3 = (α – β)3 + 3αβ(α – β)