AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration Ex 10.1 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration Exercise 10.1
10th Class Maths 10th Lesson Mensuration Ex 10.1 Textbook Questions and Answers
Question 1.
A joker’s cap is in the form of right circular cone whose base radius is 7 cm and height is 24 cm. Find the area of the sheet required to make 10 such caps.
Answer:
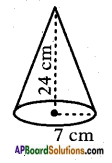
Radius of the cap (r) = 7 cm
Height of the cap (h) = 24 cm
Slant height of the cap (l) = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{7^{2}+24^{2}}\)
= \(\sqrt{49+576}\)
= √625
= 25
∴ l = 25 cm.
Lateral surface area of the cap = Cone = πrl
L.S.A. = \(\frac{22}{7}\) × 7 × 25 = 550 cm2.
∴ Area of the sheet required for 10 caps = 10 x 550 = 5500 cm2.
![]()
Question 2.
A sports company was ordered to prepare 100 paper cylinders without caps for shuttle cocks. The required dimensions of the cylinder are 35 cm length / height and its radius is 7 cm. Find the required area of thin paper sheet needed to make 100 cylinders.
Answer:
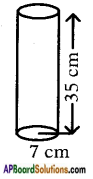
Radius of the cylinder, r = 7 cm
Height of the cylinder, h = 35 cm
T.S.A. of the cylinder with lids at both ends = 2πr(r+h)
= 2 × \(\frac{22}{7}\) × 7 × (7 + 35)
= 2 × \(\frac{22}{7}\) × 7 × 42 = 1848 cm2.
Area of thin paper required for 100 cylinders = 100 × 1848
= 184800 cm2
= \(\frac{184800}{100 \times 100}\) m2
= 18.48 m2.
Question 3.
Find the volume of right circular cone with radius 6 cm. and height 7 cm.
Answer:
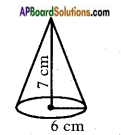
Base radius of the cone (r) = 6 cm.
Height of the cone (h) = 7 cm
Volume of the cone = \(\frac{1}{3}\)πr2h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 6 × 6 × 7
= 264 c.c. (Cubic centimeters)
∴ Volume of the right circular cone = 264 c.c.
![]()
Question 4.
The lateral surface area of a cylinder is equal to the curved surface area of a cone. If their base be the same, find the ratio of the height of the cylinder to slant height of the cone.
Answer:
Base of cylinder and cone be the same.
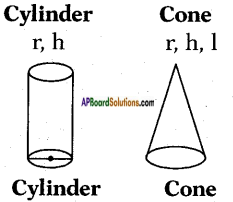
CSA / LSA of cylinder = 2πrh
CSA of cone = πrl
The lateral surface area of a cylinder is equal to the curved surface area of cone.
∴ 2πrh = πrl
⇒ \(\frac{h}{l}=\frac{\pi r}{2 \pi r}\)
⇒ \(\frac{h}{l}\) = \(\frac{1}{2}\)
∴ h : l = 1 : 2
Question 5.
A self help group wants to manufacture joker’s caps (conical caps) of 3 cm radius and 4 cm height. If the available colour paper sheet is 1000 cm2, then how many caps can be manufactured from that paper sheet?
Answer:
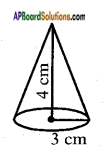
Radius of the cap (conical cap) (r) = 3 cm
Height of the cap (h) = 4 cm
Slant height l = \(\sqrt{r^{2}+h^{2}}\)
(by Pythagoras theorem)
= \(\sqrt{3^{2}+4^{2}}\)
= \(\sqrt{9+16}\)
= √25
= 5 cm
C.S.A. of the cap = πrl
= \(\frac{22}{7}\) × 3 × 5
≃ 47.14 cm2
Number of caps that can be made out of 1000 cm2 = \(\frac{1000}{47.14}\) ≃ 21.27
∴ Number of caps = 21.
![]()
Question 6.
A cylinder and cone have bases of equal radii and are of equal heights. Show that their volumes are in the ratio of 3 : 1.
Answer:
Given dimensions are:
Cone:
Radius = r
Height = h
Volume (V) = \(\frac{1}{3}\)πr2h
Cylinder:
Radius = r
Height = h
Volume (V) = πr2h
Ratio of volumes of cylinder and cone = πr2h : \(\frac{1}{3}\)πr2h
= 1 : \(\frac{1}{3}\)
= 3 : 1
Hence, their volumes are in the ratio = 3 : 1.
Question 7.
A solid iron rod has cylindrical shape. Its height is 11 cm. and base diameter is 7 cm. Then find the total volume of 50 rods?
Answer:
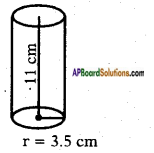
Diameter of the cylinder (d) = 7 cm
Radius of the base (r) = \(\frac{7}{2}\) = 3.5 cm
Height of the cylinder (h) = 11 cm
Volume of the cylinder V = πr2h
= \(\frac{22}{7}\) × 3.5 × 3.5 × 11 = 423.5 cm3
∴ Total volume of 50 rods = 50 × 423.5 cm3 = 21175 cm3.
![]()
Question 8.
A heap of rice is in the form of a cone of diameter 12 m. and height 8 m. Find its volume? How much canvas cloth is required to cover the heap? (Use π = 3.14)
Answer:
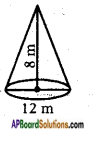
Diameter of the heap (conical) (d) = 12 cm
∴ Radius = \(\frac{d}{2}\) = \(\frac{12}{2}\) = 6 cm
Height of the cone (h) = 8 m
Volume of the cone, V = \(\frac{1}{3}\)πr2h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 6 × 6 × 8
= 301.71 m3.
Question 9.
The curved surface area of a cone is 4070 cm2 and its diameter is 70 cm. What is its slant height?
Answer:
C.S.A. of a cone = πrl = 4070 cm2
Diameter of the cone (d) = 70 cm
Radius of the cone = r = \(\frac{d}{2}\) = \(\frac{70}{2}\) = 35 cm
Let its slant height be ‘l’.
By problem,
πrl = 4070 cm2
\(\frac{22}{7}\) × 35 × l = 4070
110 l = 4070
l = \(\frac{4070}{110}\) = 37 cm
∴ Its slant height = 37 cm.