AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 10 Mensuration Ex 10.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 10th Lesson Mensuration Exercise 10.2
10th Class Maths 10th Lesson Mensuration Ex 10.2 Textbook Questions and Answers
Question 1.
A toy is in the form of a cone mounted on a hemisphere. The diameter of the base and the height of the cone are 6 cm and 4 cm respectively. Determine the surface area of the toy. (Use π = 3.14)
Answer:
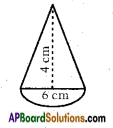
Diameter of the base of the cone d = 6 cm.
∴ Radius of the base of the cone
r = \(\frac{d}{2}\) = \(\frac{6}{2}\) = 3 cm
Height of the cone = h = 4 cm
Slant height of the cone l = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{3^{2}+4^{2}}\)
= \(\sqrt{9+16}\)
= √25
= 5 cm
∴ C.S.A of the cone = πrl
= \(\frac{22}{7}\) × 3 × 5
= \(\frac{330}{7}\) cm2
Radius of the hemisphere = \(\frac{d}{2}\) = \(\frac{6}{2}\) = 3 cm
C.S.A. of the hemisphere = 2πr2
= 2 × \(\frac{22}{7}\) × 3 × 3
= \(\frac{396}{7}\)
Hence the surface area of the toy = C.S.A. of cone + C.S.A. of hemisphere
= \(\frac{330}{7}\) + \(\frac{396}{7}\)
= \(\frac{726}{7}\) ≃ 103.71 cm2.
![]()
Question 2.
A solid is in the form of a right circular cylinder with a hemisphere at one end and a cone at the other end. The radius of the common base is 8 cm and the heights of the cylindrical and conical portions are 10 cm and 6 cm respectively. Find the total surface area of the solid. [Use π = 3.14]
Answer:
Total surface area = C.S.A. of the cone + C.S.A. of cylinder + C.S.A of the hemisphere.
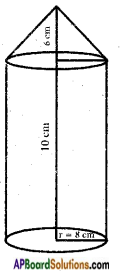
Cone:
Radius (r) = 8 cm
Height (h) = 6 cm
Slant height l = \(\sqrt{r^{2}+h^{2}}\)
= \(\sqrt{8^{2}+6^{2}}\)
= \(\sqrt{64+36}\)
= √100
= 10 cm
C.S.A. = πrl
= \(\frac{22}{7}\) × 8 × 10
= \(\frac{1760}{7}\) cm2
Cylinder:
Radius (r) = 8 cm;
Height (h) = 10 cm
C.S.A. = 2πrh
= 2 × \(\frac{22}{7}\) × 8 × 10
= \(\frac{3520}{7}\) cm2
Hemisphere:
Radius (r) = 8 cm
C.S.A. = 2πr2
= 2 × \(\frac{22}{7}\) × 8 × 8
= \(\frac{2816}{7}\) cm2
∴ Total surface area of the given solid
= \(\frac{1760}{7}\) + \(\frac{3520}{7}\) + \(\frac{2816}{7}\)
T.S.A. = \(\frac{8096}{7}\) = 1156.57 cm2.
![]()
Question 3.
A medicine capsule is ih the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the capsule is 14 mm. and the width is 5 mm. Find its surface area.
Answer:
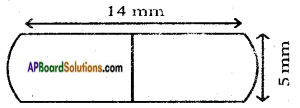
Surface area of the capsule = C.S.A. of 2 hemispheres + C.S.A. of the cylinder
i) Now for Hemisphere:
Radius (r) = \(\frac{d}{2}\) = \(\frac{5}{2}\) = 2.5 mm
C.S.A of each hemisphere = 2πr2
C.S.A of two hemispheres
= 2 × 2πr2 = 4πr2
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\) × \(\frac{5}{2}\)
= \(\frac{550}{7}\)
= 78.57 mm2.
ii) Now for Cylinder:
Length of capsule = AB =14 mm
Then height (length) cylinder part = 14 – 2(2.5)
h = 14 – 5 = 9 mm
Radius of cylinder part (r) = \(\frac{5}{2}\)
Now C.S.A of cylinder part = 2πrh
= 2 × \(\frac{22}{7}\) × \(\frac{5}{2}\) × 9
= \(\frac{900}{7}\)
= 141.428 mm2
Now total surface area of capsule
= 78.57 + 141.43 = 220 mm2
Question 4.
Two cubes each of volume 64 cm3 are joined end to end together. Find the surface area of the resulting cuboid.
Answer:
Given, volume of the cube.
V = a3 = 64 cm3
∴ a3 = 4 × 4 × 4 = 43 , Hence a = 4 cm
When two cubes are added, the length of cuboid = 2a = 2 × 4 = 8 cm,
breadth = a = 4 cm.
height = a = 4 cm is formed.
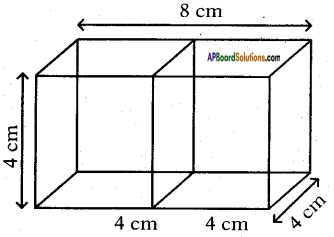
∴ T.S.A. of the cuboid
= 2 (lb + bh + lh)
= 2(8 × 4 + 4 × 4 + 8 × 4)
= 2(32 + 16 + 32)
= 2 × 80
= 160 cm2
∴ The surface area of resulting cuboid is 160 cm2.
![]()
Question 5.
A storage tank consists of a circular cylinder with a hemisphere stuck on either end. If the external diameter of the cylinder be 1.4 m. and its length be 8 m. Find the cost of painting it on the outside at rate of Rs. 20 per m2.
Answer:
Total surface area of the tank = 2 × C.S.A. of hemisphere + C.S.A. of cylinder.
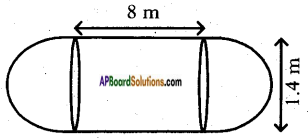
Hemisphere:
Radius (r) = \(\frac{d}{2}\) = \(\frac{1.4}{2}\) = 0.7 m
C.S.A. of hemisphere = 2πr2
= 2 × \(\frac{22}{7}\) × 0.7 × 0.7
= 3.08 m2.
2 × C.S.A. = 2 × 3.08 m2 = 6.16 m2
Cylinder:
Radius (r) = \(\frac{d}{2}\) = \(\frac{1.4}{2}\) = 0.7 m
Height (h) = 8 m
C.S.A. of the cylinder = 2πrh
= 2 × \(\frac{22}{7}\) × 0.7 × 8
= 35.2 m2
∴ Total surface area of the storage tank = 35.2 + 6.16 = 41.36 m2
Cost of painting its surface area @ Rs. 20 per sq.m, is
= 41.36 × 20 = Rs. 827.2.
Question 6.
A hemisphere is cut out from one face of a cubical wooden block such that the diameter of the hemisphere is equal to the length of the cube. Determine the surface area of the remaining solid.
Answer:
Let the length of the edge of the cube = a units
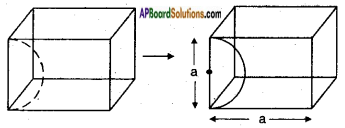
T.S.A. of the given solid = 5 × Area of each surface + Area of hemisphere
Square surface:
Side = a units
Area = a2 sq. units
5 × square surface = 5a2 sq. units
Hemisphere:
Diameter = a units;
Radius = \(\frac{a}{2}\)
C.S.A. = 2πr2
= 2π\(\left(\frac{a}{2}\right)^{2}\)
= 2π\(\frac{a^{2}}{4}\) = \(\frac{\pi \mathrm{a}^{2}}{2}\) sq. units
Total surface area = 5a2 + \(\frac{\pi \mathrm{a}^{2}}{2}\) = a2\(\left(5+\frac{\pi}{2}\right)\) sq. units.
![]()
Question 7.
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown in the figure. If the height of the cylinder is 10 cm and its base radius is of 3.5 cm, find the total surface area of the article.

Answer:
Surface area of the given solid = C.S.A. of the cylinder + 2 × C.S.A. of hemisphere.
If we take base = radius
Cylinder:
Radius (r) = 3.5 cm
Height (h) = 10 cm
C.S.A. = 2πrh
= 2 × \(\frac{22}{7}\) × 3.5 × 10
= 220 cm2
Hemisphere:
Radius (r) = 3.5 cm
C.S.A. = 2πr2
= 2 × \(\frac{22}{7}\) × 3.5 × 3.5
= 77 cm2
2 × C.S.A. = 2 × 77 = 154 cm2
∴ T.S.A. = 220 + 154 = 374 cm2.