AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 5 Quadratic Equations Ex 5.4 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 5th Lesson Quadratic Equations Exercise 5.4
10th Class Maths 5th Lesson Quadratic Equations Ex 5.4 Textbook Questions and Answers
Question 1.
Find the nature of the roots of the following quadratic equations. If real roots exist, find them.
i) 2x2 – 3x + 5 = 0
Answer:
Given: 2x2 – 3x + 5 = 0
a = 2; b = -3; c = 5
Discriminant = b2 – 4ac
b2 – 4ac = (-3)2 – 4(2)(5)
= 9 – 40
= -31 < 0
∴ Roots are imaginary.
ii) 3x2 – 4√3x + 4 = 0
Answer:
Given: 3x2 – 4√3x + 4 = 0
a = 3; b = -4√3; c = 4
b2 – 4ac = (-4√3)2 – 4(3)(4)
= 48 – 48 = 0
∴ Roots are real and equal and they
\(\frac{-b}{2a}\), \(\frac{-b}{2a}\)
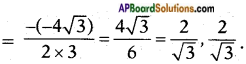
![]()
iii) 2x2 – 6x + 3 = 0
Answer:
Given: 2x2 – 6x + 3 = 0
a = 2; b = -6; c = 3
b2 – 4ac = (-6)2 – 4(2)(3)
= 36 – 24
= 12 > 0
∴ The roots are real and distinct. They are

Question 2.
Find the values of k for each of the fol-lowing quadratic equations so that they have two equal roots.
i) 2x2 + kx + 3 = 0
Answer:
Given : 2x2 + kx + 3 = 0 has equal roots
∴ b2 – 4ac = 0
Here a = 2; b = k; c = 3
b2 – 4ac = (k)2 – 4(2)(3) = 0
⇒ k2 – 24 = 0
⇒ k2 = 24
⇒ k = √24 = ± 2√6
ii) kx(x – 2) + 6 = 0
Answer:
Given: kx(x – 2) + 6 = 0
kx2 – 2kx + 6 = 0
As this Q.E. has equal roots,
b2 – 4ac = 0
Here
a = k; b = -2k; c = 6
∴ b2 – 4ac = (-2k)2 – 4(k)(6) = 0
⇒ 4k2 – 24k = 0
⇒ 4k(k – 6) = 0
⇒ 4k = 0 (or) k – 6 = 0
⇒ k = 0 (or) 6
But k = 0 is trivial
∴ k = 6.
![]()
Question 3.
Is it possible to design a rectangular mango grove whose length is twice its breadth, and the area is 800 m2? If so, find its length and breadth.
Answer:
Let the breadth = x m
Then length = 2x m
Area = length x breadth = x.(2x)
= 2x2 m2
By problem 2x2 = 800 ⇒ x2 = 400
and x = √400 = ± 20
∴ Breadth x = 20 m and
length 2x = 2 × 20 = 40 m.
Question 4.
The sum of the ages of two friends is 20 years. Four years ago, the product of their ages in years was 48. Is the above situation possible? If so, deter¬mine their present ages.
Answer:
Let the age one of the two friends be x years.
Then the age of the other = 20 – x
Then, 4 years ago their ages would be (x – 4) and (20 – x – 4) = 16 – x
∴ Product of their ages 4 years ago = (x – 4) (16 – x)
By problem (x – 4) (16 – x) = 48
⇒ x(16 – x) – 4(16 – x) = 48
⇒ 16x – x2 – 64 + 4x = 48
⇒ x2 – 20x + 112 = 0
Here a = 1; b = -20; c = 112
b2 – 4ac = (-20)2 – 4(1) (112)
= 400 – 448
= -48 < 0
Thus the roots are not real.
∴ The situation is not possible.
![]()
Question 5.
Is it possible to design a rectangular park of perimeter 80 m and area 400 m2? If so, find its length and breadth.
Answer:
Given: Perimeter of a rectangle 2(1 + b) = 80
⇒ 6 + b = \(\frac{80}{2}\) = 40
Area of the rectangle, l × b = 400
If possible, let us suppose that length of the rectangle = x m say
Then its breadth by equation (1) = 40 – x
By problem area = x . (40 – x) = 400
⇒ 40x – x2 = 400
⇒ x2 – 40x + 400 = 0
Here a = 1; b = -40; c = +400
b2 – 4ac = (-40)2 – 4(1)(+400)
= 1600 – 1600 = 0
∴ The roots are real and equal.
They are \(\frac{-b}{2a}\), \(\frac{-b}{2a}\)
i.e., \(\frac{-(-40)}{2 \times 1}\) = \(\frac{40}{2}\) = 20
∴ The dimensions are 20 m, 20 m.
(∴ The park is in square shape)