AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 7 Coordinate Geometry Ex 7.2 Textbook Questions and Answers.
AP State Syllabus SSC 10th Class Maths Solutions 7th Lesson Coordinate Geometry Exercise 7.2
10th Class Maths 7th Lesson Coordinate Geometry Ex 7.2 Textbook Questions and Answers
Question 1.
Find the coordinates of the point which divides the line segment joining the points (-1, 7) and (4, -3) in the ratio 2 :3.
Answer:
Given points P (-1, 7) and Q (4, – 3). Let ‘R’ be the required point which divides \(\overline{\mathrm{PQ}}\) in the ratio 2:3. Then
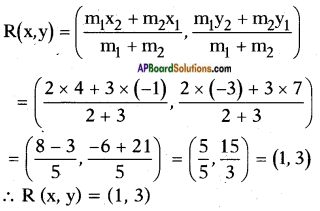
![]()
Question 2.
Find the coordinates of the points of trisection of the line segment joining (4, -1) and (-2, -3).
Answer:
Given points A (4, – 1) and B (- 2, – 3) Let P and Q be the points of trisection
of \(\overline{\mathrm{AB}}\), then AP = PQ = QB.

∴ P divides \(\overline{\mathrm{AB}}\) internally in the ratio 1 : 2.

Also, Q divides \(\overline{\mathrm{AB}}\) in the ratio 2 : 1 internally.
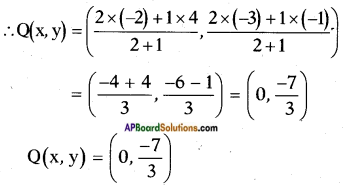
Question 3.
Find the ratio in which the line segment joining the points (-3, 10) and (6, -8) is divided by (-1, 6).
Answer:
Let the point (-1, 6) divides the line segment joining the points (-3, 10) and (6, -8) in a ratio of m : n
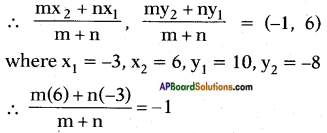
⇒ 6m – 3n = -(m + n) = -m – n
⇒ 6m + m = – n + 3n
⇒ 7m = 2n
⇒ \(\frac{m}{n}=\frac{2}{7}\)
⇒ m : n = 2 : 7
∴ The point (-1, 6) divides the given line segment in a ratio of 2 : 7.
![]()
Question 4.
If (1, 2), (4, y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y.
Answer:
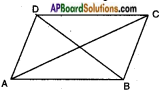
Given: ▱ ABCD is a parallelogram where A (1, 2), B (4, y), C (x, 6) and D (3, 5).
In a parallelogram, diagonals bisect each other.
i.e., the midpoints of the diagonals coincide with each other.
i.e.,midpoint of AC = midpoint of BD
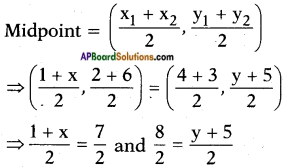
⇒ 1 + x = 7 and 8 = y + 5
⇒ x = 7 – 1 and y = 8 – 5
∴ x = 6 and y = 3.
Question 5.
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).
Answer:
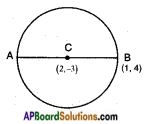
Given:
A circle with centre ‘C’ (2, -3). \(\overline{\mathrm{AB}}\) is a diameter where
B = (1, 4); A = (x, y).
C is the midpoint of AB.
[∵ Centre of a circle is the midpoint of the diameter]
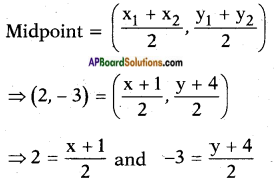
4 = x + 1 and – 6 = y + 4
⇒ x = 4 – 1 = 3 and y = -6 – 4 = -10
A (x, y) = (3, -10)
![]()
Question 6.
If A and B are (-2, -2) and (2, -4) respectively. Find the coordinates of P such that AP = \(\frac{3}{7}\) AB and P lies on the segment AB.
Answer:
Given: A (- 2, – 2) and B (2, – 4)
P lies on AB such that AP = latex]\frac{3}{7}[/latex] AB
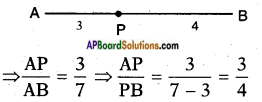
i.e., P divides \(\overline{\mathrm{AB}}\) in the ratio 3 : 4 By section formula,
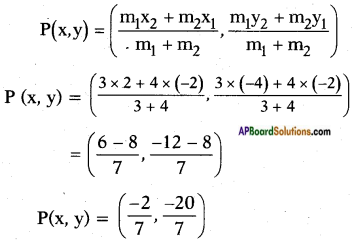
Question 7.
Find the coordinates of points which divide the line segment joining A (-4, 0) and B (0, 6) into four equal parts.
Answer:
Given, A (- 4, 0) and B (0, 6).
Let P, Q and R be the points which divide AB into four equal parts.

P divides \(\overline{\mathrm{AB}}\) in the ratio 1 : 3, Q → 1 : 1 and R → 3 : 1 Use section formula to find P, Q and R.
Then, Q is the midpoint of \(\overline{\mathrm{AB}}\)
P is the midpoint of \(\overline{\mathrm{AQ}}\)
R is the midpoint of \(\overline{\mathrm{QB}}\)
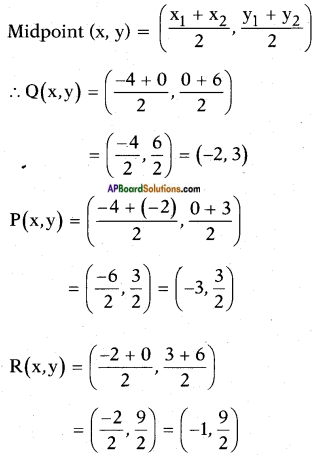
![]()
Question 8.
Find the coordinates of the points which divides the line segment joining A(-2, 2) and B(2, 8) into four equal parts.
Answer:
Given, A (- 2, 2) and B (2, 8).
Let P, Q and R be the points which divide AB into four equal parts.

Then, Q is the midpoint of \(\overline{\mathrm{AB}}\)
P is the midpoint of \(\overline{\mathrm{AQ}}\)
R is the midpoint of \(\overline{\mathrm{QB}}\)
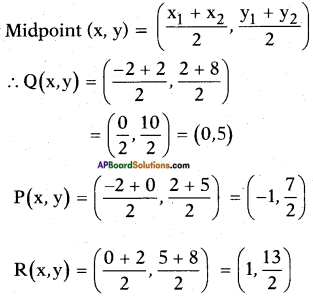
Question 9.
Find the coordinates of the point which divide the line segment joining the points (a + b, a-b) and (a-b, a + b) in the ratio 3 : 2 internally.
Answer:
Given : A (a + b, a – b) and B (a – b, a + b).
Let P (x, y) divides \(\overline{\mathrm{AB}}\) in the ratio 3 : 2 internally.
Section formula
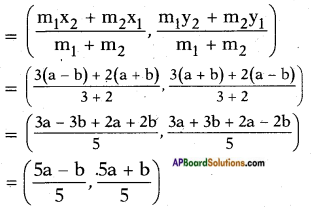
Question 10.
Find the coordinates of centroid of the triangle with following vertices:
i) (-1, 3), (6, -3) and (-3, 6)
Answer:
Given: △ABC in which- A (- 1, 3), B (6, -3) and C (-3, 6)

ii) (6, 2), (0, 0) and (4, -7)
Answer:
Given: The three vertices of a triangle are A (6, 2), B (0, 0) and C (4, – 7).
Centroid (x, y)

![]()
iii) (1,-1), (0, 6) and (-3, 0)
Answer:
Given: (1, -1), (0, 6) and (-3, 0) are the vertices of a triangle.
Centroid (x, y)
