AP SSC 10th Class Maths Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1

AP State Board Syllabus AP SSC 10th Class Maths Textbook Solutions Chapter 9 Tangents and Secants to a Circle Ex 9.1 Textbook Questions and Answers.

AP State Syllabus SSC 10th Class Maths Solutions 9th Lesson Tangents and Secants to a Circle Exercise 9.1

10th Class Maths 9th Lesson Tangents and Secants to a Circle Ex 9.1 Textbook Questions and Answers

Question 1.
Fill in the blanks.
i) A tangent to a circle intersects it in ——— point(s). (one)
ii) A line intersecting a circle in two points is called a ———. (secant)
iii) The number of tangents drawn at the end of the diameter is ———. (two)
iv) The common point of a tangent to a circle and the circle is called ———. (point of contact)
v) We can draw ——— tangents to a given circle. (infinite)

Question 2.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm. Find length of PQ.
Answer:
Given: A circle with centre O and radius OP = 5 cm
\(\overline{\mathrm{PQ}}\) is a tangent and OQ = 12 cm
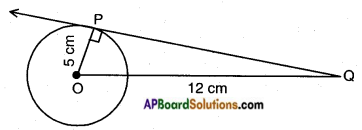We know that ∠OPQ = 90°
Hence in △OPQ
OQ² = OP² + PQ²
[∵ hypotenuse² = Adj. side² + Opp. side²]
12² = 5² + PQ²
∴ PQ² = 144 – 25 .
PQ² = 119
PQ = √119

Question 3.
Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
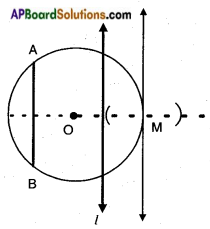Steps:

1. Draw a circle with some radius.
2. Draw a chord of the circle.
3. Draw a line parallel to the chord intersecting the circle at two distinct points.
4. This is secant of the circle (l).
5. Draw another line parallel to the chord, just touching the circle at one point (M). This is a tangent of the circle.

Question 4.
Calculate the length of tangent from a point 15 cm. away from the centre of a circle of radius 9 cm.
Answer:
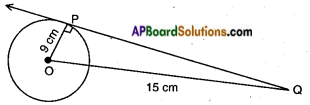Given: A circle with radius OP = 9 cm
A tangent PQ from a point Q at a distance of 15 cm from the centre, i.e., OQ =15 cm
Now in △POQ, ∠P = 90°
OP² + PQ² – OQ²
9² + PQ² = 15²
PQ² = 15² – 9²
PQ² = 144
∴ PQ = √144 = 12 cm.
Hence the length of the tangent =12 cm.

Question 5.
Prove that the tangents to a circle at the end points of a diameter are parallel.
Answer:
A circle with a diameter AB.
PQ is a tangent drawn at A and RS is a tangent drawn at B.
R.T.P: PQ || RS.
Proof: Let ‘O’ be the centre of the circle then OA is radius and PQ is a tangent.
∴ OA ⊥ PQ ……….(1)
[∵ a tangent drawn at the end point of the radius is perpendicular to the radius]
Similarly, OB ⊥ RS ……….(2)
[∵ a tangent drawn at the end point of the radius is perpendicular to the radius]
But, OA and OB are the parts of AB.
i.e., AB ⊥ PQ and AB ⊥ RS.
∴ PQ || RS.
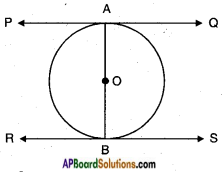O is the centre, PQ is a tangent drawn at A.
∠OAQ = 90°
Similarly, ∠OBS = 90°
∠OAQ + ∠OBS = 90° + 90° = 180°
∴ PQ || RS.
[∵ Sum of the consecutive interior angles is 180°, hence lines are parallel]