Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Addition of Vectors Solutions Exercise 4(a)
I.
Question 1.
ABCD is a Parallelogram. If L and M are the middle points of BC and CD, respectively, then find (i) AL and AM in terms of AB and AD (ii) λ, if AM = λ AD – LM.
Solution:



Question 2.
In ∆ABC, P, Q, and R are the midpoints of the sides AB, BC, and CA respectively. If D is any point.
(i) then express \(\overline{\mathrm{DA}}+\overline{\mathrm{DB}}+\overline{\mathrm{DC}}\) interms of \(\overline{D P}\), \(\overline{D Q}\) and \(\overline{D R}\).
(ii) If \(\overline{\mathbf{P A}}+\overline{\mathbf{Q B}}+\overline{\mathbf{R C}}=\bar{\alpha}\) then find \(\bar{\alpha}\)
Solution:

![]()
Question 3.
Let \(\overline{\mathbf{a}}=\overline{\mathbf{i}}+2 \overline{\mathbf{j}}+3 \overline{\mathbf{k}}\) and \(\overline{\mathbf{b}}=\mathbf{3} \overline{\mathbf{i}}+\overline{\mathbf{j}}\). Find the unit vector in the direction of \(\overline{\mathbf{a}}+\overline{\mathbf{b}}\).
Solution:

Question 4.
If the vectors \(-3 \overline{\mathbf{i}}+4 \bar{j}+\lambda \overline{\mathbf{k}}\) and \(\mu \bar{i}+8 \bar{i}+6 \bar{k}\) are coilinear vectors , then find λ and µ.
Solution:

Question 5.
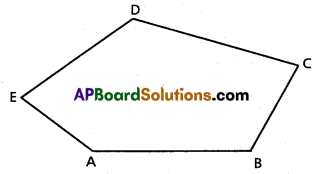
ABCDE is a pentagon. If the sum of the vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AE}}, \overline{\mathrm{BC}}, \overline{\mathrm{DC}}, \overline{\mathrm{ED}}\) and \(\overline{\mathbf{A C}}\) is λ \(\overline{\mathbf{A C}}\), then find the value of λ.
Solution:

Question 6.
If the position vectors of the points A, B and C are \(-2 \overline{\mathbf{i}}+\overline{\mathbf{j}}-\overline{\mathbf{k}},-4 \overline{\mathbf{i}}+2 \overline{\mathbf{j}}+2 \overline{\mathbf{k}}\) and \(6 \bar{i}-3 \bar{j}-13 \bar{k}\) respectively and \(\overline{\mathbf{A B}}=\lambda \overline{\mathrm{AC}}\), then find the value of λ.
Solution:

Question 7.
If \(\overline{\mathrm{OA}}=\overline{\mathbf{i}}+\overline{\mathbf{j}}+\overline{\mathbf{k}}, \overline{\mathrm{AB}}=3 \bar{i}-2 \overline{\mathbf{j}}+\overline{\mathbf{k}}\), \(\overline{B C}=\bar{i}+2 \bar{j}-2 \bar{k}\) and \(\overline{C D}=2 \bar{i}+\bar{j}+3 \bar{k}\), then find the vector \(\overline{O D}\).
Solution:
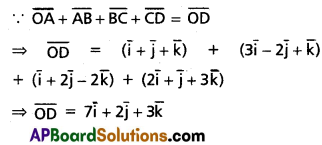
![]()
Question 8.
\(\overline{\mathbf{a}}=2 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}+\overline{\mathbf{k}}\) and \(\bar{b}=4 \bar{i}+m \bar{j}+n \bar{k}\) are collinear vectors, then find m and n.
Solution:

Question 9.
Let \(\bar{a}=2 \bar{i}+4 \overline{\mathbf{j}}-5 \overline{\mathbf{k}}, \bar{b}=\hat{i}+\bar{j}+\bar{k}\) and \(\bar{c}=\bar{j}+2 \bar{k}\). Find the unit vector in the opposite direction of \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}\).
Solution:

Question 10.
Is the triangle formed by the vectors \(3 \bar{i}+5 \bar{j}+2 \bar{k}, 2 \bar{i}-3 \bar{j}-5 \bar{k}\) and \(-5 \bar{i}-2 \bar{j}+3 \bar{k}\) equilateral?
Solution:

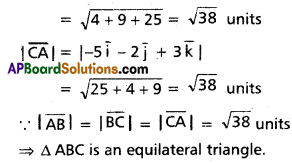
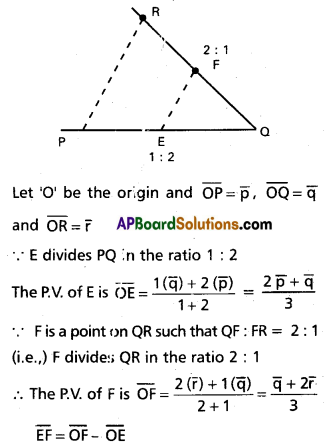
Question 11.
If α, β and γ be the angles made by the vector \(3 \bar{i}-6 \bar{i}+2 \bar{k}\) with the positive directions of the co-ordinate axes, then find cos α, cos β, cos γ.
Solution:
Unit vectors along the co-ordinate axes are respectively \(\bar{i}, \bar{j}, \bar{k}\).

Question 12.
Find the angles made by the straight line passing through the points (1, -3, 2) and (3, -5, 1) with the co-ordinate axes.
Solution:
Unit vectors along the co-ordinate axes are respectively \(\bar{i}, \bar{j}, \bar{k}\).
Let A(1, -3, 2) and B(3, -5, 1) be two given points.
Let ‘O’ be the origin. Then

II.
Question 1.
If \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}=\alpha \overline{\mathbf{d}}, \overline{\mathbf{b}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}=\beta \overline{\mathbf{a}}\) and \(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathrm{c}}\) are non-coplanar vectors, then show that \(\overline{\mathbf{a}}+\overline{\mathbf{b}}+\overline{\mathbf{c}}+\overline{\mathbf{d}}=\mathbf{0}\).
Solution:


![]()
Question 2.
\(\overline{\mathbf{a}}, \overline{\mathbf{b}}, \overline{\mathbf{c}}\) are non-coplanar vectors. Prove that the following four points are coplanar.
(i) \(-\overline{\mathbf{a}}+4 \overline{\mathbf{b}}-3 \bar{c}, \quad 3 \bar{a}+2 \bar{b}-5 \bar{c}\), \(-3 \overline{\mathbf{a}}+8 \overline{\mathbf{b}}-5 \overline{\mathbf{c}},-3 \overline{\mathbf{a}}+2 \overline{\mathbf{b}}+\overline{\mathbf{c}}\)
Solution:
Let ‘O’ be the origin and A, B, C, D be the four points.


4 + 2x + 2y = 0 ……..(1)
-2 – 4x + 2y = 0 ……..(2)
-2 + 2x – 4y = 0 …….(3)
Solve (1) and (3)
6y + 6 = 0 ⇒ y = -1
Substitute in (1)
2x + 2 (-1) + 4 = 0
⇒ 2x + 2 = 0
⇒ x = -1
Substitute x = -1, y = -1 in (2)
-2 – 4(-1) + 2(-1) = -4 + 4 = 0
∴ The vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}, \overline{\mathrm{AD}}\) are coplanar
⇒ A, B, C, D are coplanar
Hence the given points are coplanar.
(ii) \(6 \bar{a}+2 \bar{b}-\bar{c}, 2 \bar{a}-\bar{b}+3 \bar{c},-\bar{a}+2 \bar{b}-4 \bar{c},\)\(-12 \bar{a}-\bar{b}-3 \bar{c}\)
Solution:
Let O be the origin. Let A, B, C, D be the given points.

Let us suppose that one vector can be expressed as a linear combination of the other two.
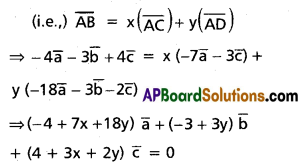
∵ \(\bar{a}, \bar{b}, \bar{c}\) are non-coplanar vectors.
7x + 18y – 4 = 0 ………(1)
-3 + 3y = 0 ⇒ y = 1 …….(2)
3x + 2y + 4 = 0 ………(3)
Substitute y =1 in (3)
3x + 2 + 4 = 0 ⇒ x = -2
Substitute x = -2 and y = 1 in (1)
7(-2) + 18(1) – 4 = 0 ⇒ 0 = 0
Hence \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}\) and \(\overline{\mathrm{AD}}\) are coplanar.
⇒ The points A, B, C, D are coplanar.
Question 3.
If \(\overline{\mathbf{i}}, \overline{\mathbf{j}}, \overline{\mathbf{k}}\) are unit vectors along the positive directions of the coordinate axes, then show that the four points \(4 \overline{\mathbf{i}}+5 \overline{\mathbf{j}}+\overline{\mathbf{k}},-\overline{\mathbf{j}}-\overline{\mathbf{k}}, 3 \overline{\mathbf{i}}+9 \overline{\mathbf{j}}+4 \overline{\mathbf{k}}\) and \(-4 \bar{i}+4 \bar{j}+4 \bar{k}\) are coplanar.
Solution:
Let ‘O’ be the origin and let A, B, C, D be the given points.


⇒ The given points A, B, C, D are coplanar.
Second Method:
\(\left[\begin{array}{lll}
\overline{\mathrm{AB}} & \overline{\mathrm{AC}} & \overline{\mathrm{AD}}
\end{array}\right]\) = \(\left|\begin{array}{ccc}
-4 & -6 & -2 \\
-1 & 4 & 3 \\
-8 & -1 & 3
\end{array}\right|\)
= -4(12 + 3) + 6(-3 + 24) – 2(1 + 32)
= -60 + 126 – 66
= 0
Hence the vectors \(\overline{\mathrm{AB}}, \overline{\mathrm{AC}}\) and \(\overline{\mathrm{AD}}\) are coplanar.
⇒ The given points A, B, C, D are coplanar.
![]()
Question 4.
If a, b, c are non-coplanar vectors, then test for the collinearity of the following points whose position vectors are given by
(i) \(\bar{a}-2 \bar{b}+3 \bar{c}, 2 \bar{a}+3 \bar{b}-4 \bar{c},-7 \bar{b}+10 \bar{c}\)
Solution:
Let ‘O’ be the origin. A, B, C be the given points.
Then \(\overline{\mathrm{OA}}=\overline{\mathrm{a}}-2 \overline{\mathrm{b}}+3 \overline{\mathrm{c}}\)

(ii) \(3 \bar{a}-4 \bar{b}+3 \bar{c}\), \(-4 \bar{a}+5 \bar{b}-6 \bar{c}\), \(4 \overline{\mathbf{a}}-7 \overline{\mathbf{b}}+6 \overline{\mathbf{c}}\)
Solution:

(iii) \(\begin{aligned}
&2 \bar{a}+5 \bar{b}-4 \bar{c}, \bar{a}+4 \bar{b}-3 \bar{c}, \\
&4 \bar{a}+7 \bar{b}-6 \bar{c}
\end{aligned}\)
Solution:
Let ‘O’ be the origin and A, B, C be the given points.
Then \(\overline{\mathrm{OA}}=2 \overline{\mathrm{a}}+5 \overline{\mathrm{b}}-4 \overline{\mathrm{c}}\), \(\overline{\mathrm{OB}}=\overline{\mathrm{a}}+4 \overline{\mathrm{b}}-3 \overline{\mathrm{c}}\)

∴ The points A, B, C are collinear.
III.
Question 1.
In the Cartesian plane, O is the origin of the coordinate axes. A person starts at O and walks a distance of 3 units in the NORTH-EAST direction and reaches point P. From P he walks 4 units of distance parallel to NORTH-WEST direction and reaches the point Q. Express the vector \(\overline{\mathbf{O Q}}\) in terms of \(\overline{\mathbf{i}}\) and \(\overline{\mathbf{j}}\) (observe that ∠XOP = 45°)
Solution:
‘O’ the origin of co-ordinate axes.
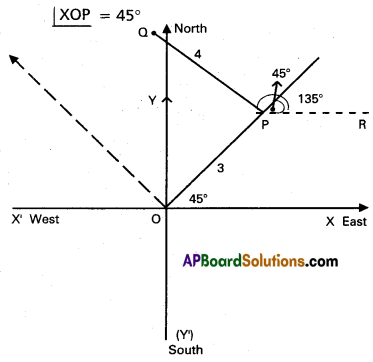

Question 2.
The points O, A, B, X and Y are such that \(\overline{\mathbf{O A}}=\overline{\mathbf{a}}, \overline{\mathbf{O B}}=\overline{\mathbf{b}}, \overline{\mathbf{O X}}=\mathbf{3} \overline{\mathbf{a}}\) and \(\overline{\mathbf{O Y}}=\mathbf{3} \overline{\mathbf{b}}\). Find \(\overline{\mathbf{B X}}\) and \(\overline{\mathbf{A Y}}\) interms of \(\bar{a}\) and \(\bar{b}\). Futher, if the point P divides AY in the ratio 1 : 3, then express \(\overline{\mathrm{BP}}\) interms of \(\bar{a}\) and \(\bar{a}\).
Solution:
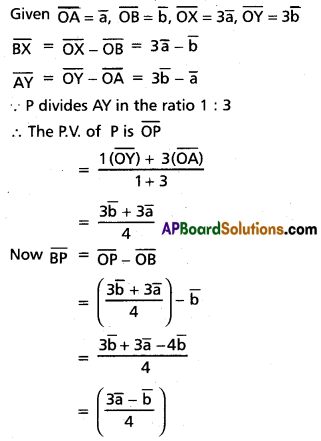
Question 3.
If ∆OAB, E is the midpoint of AB and F is a point on OA such that OF = 2(FA). If C is the point of intersection of \(\overline{\mathrm{OE}}\) and \(\overline{\mathrm{BF}}\), then find the ratios OC : CE and BC : CF.
Solution:
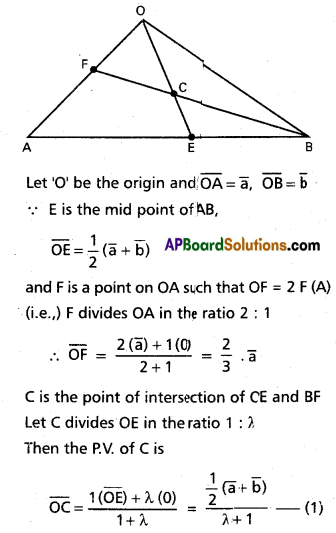


![]()
Question 4.
Point E divides the segment PQ internally in the ratio 1 : 2 and R is any point not on the line PQ. If F is a point on QR such that QF : FR = 2 : 1, then show that EF is parallel to PR.
Solution: