Inter 1st Year Maths 1A Functions Solutions Ex 1(b)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Functions Solutions Exercise 1(b) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Functions Solutions Exercise 1(b)

I.

Question 1.
If f(x) = e^x and g(x) = log_ex, then show that f o g = g o f and find f^-1 and g^-1.
Solution:
Given f(x) = e^x and g(x) = log_ex
Now (f o g) (x) = f(g(x))
= f(log_ex) [∵ g(x) = \(\log _{e} x\)]
= \(e^{\left(\log _{e} x\right)}\)
= x
∴ (fog) (x) = x ………(1)
and (g o f) (x) = g(f(x))
= g(e^x) [∵ f(x) = e^x]
= log_e (e^x) [∵ g(x) = log_ex]
= x log_e (e)
= x(1)
= x
∴ (g o f) (x) = x …….(2)
From (1) and (2)
f o g = g o f
Given f(x) = e^x
Let y = f(x) = e^x ⇒ x = f^-1(y)
and y = e^x ⇒ x = log_e (y)
∴ f^-1(y) = log_e (y) ⇒ f^-1(x) = log_e (x)
Let y = g(x) = log_e (x)
∵ y = g(x) ⇒ x = g^-1(y)
∵ y = log_e (x) ⇒ x = e^y
∴ g^-1(y) = e^y ⇒ g^-1(x) = e^x
∴ f^-1(x) = log_e (x) and g^-1(x) = e^x

Question 2.
If f(y) = \(\frac{y}{\sqrt{1-y^{2}}}\), g(y) = \(\frac{y}{\sqrt{1+y^{2}}}\) then show that (fog) (y) = y
Solution:
f(y) = \(\frac{y}{\sqrt{1-y^{2}}}\) and g(y) = \(\frac{y}{\sqrt{1+y^{2}}}\)
Now, (fog) (y) = f(g(y))

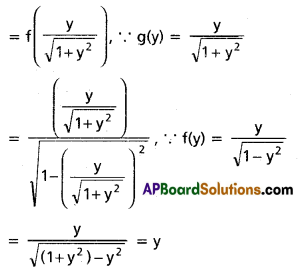
∴ (fog) (y) = y

Question 3.
If f : R → R, g : R → R are defined by f(x) = 2x² + 3 and g(x) = 3x – 2, then find
(i) (fog)(x)
(ii) (gof) (x)
(iii) (fof) (0)
(iv) go(fof) (3)
Solution:
f : R → R, g : R → R and f(x) = 2x² + 3; g(x) = 3x – 2
(i) (f o g) (x) = f(g(x))
= f(3x – 2) [∵ g(x) = 3x – 2]
= 2(3x- 2)² + 3 [∵ f(x) = 2x² + 3]
= 2(9x² – 12x + 4) + 3
= 18x² – 24x + 8 + 3
= 18x² – 24x + 11

(ii) (gof) (x) = g(f(x))
= g(2x² + 3) [∵ f(x) = 2x² + 3]
= 3(2x² + 3) – 2 [∵ g(x) = 3x – 2]
= 6x² + 9 – 2
= 6x² + 7

(iii) (fof) (0) = f(f(0))
= f(2(0) + 3) [∵ f(x) = 2x² + 3]
= f(3)
= 2(3)² + 3
= 18 + 3
= 21

(iv) g o (f o f) (3)
= g o (f (f(3)))
= g o (f (2(3)² + 3)) [∵ f(x) = 2x² + 3]
= g o (f(21))
= g(f(21))
= g(2(21)² + 3)
= g(885)
= 3(885) – 2 [∵ g(x) = 3x – 2]
= 2653

Question 4.
If f : R → R, g : R → R are defined by f(x) = 3x – 1, g(x) = x² + 1, then find
(i) (f o f) (x² + 1)
(ii) f o g (2)
(iii) g o f (2a – 3)
Solution:
f : R → R, g : R → R and f(x) = 3x – 1 ; g(x) = x² + 1
(i) (f o f) (x² + 1)
= f(f(x² + 1))
= f[3(x² + 1) – 1] [∵ f(x) = 3x – 1]
= f(3x² + 2)
= 3(3x² + 2) – 1
= 9x² + 5

(ii) (f o g) (2)
= f(g(2))
= f(2² + 1) [∵ g(x) = x² + 1]
= f(5)
= 3(5) – 1
= 14 [∵ f(x) = 3x – 1]

(iii) (g o f) (2a – 3)
= g(f(2a – 3))
= g[3(2a – 3) – 1] [∵ f(x) = 3x – 1]
= g(6a – 10)
= (6a – 10)² + 1 [∵ g(x) = x² + 1]
= 36a² – 120a + 100 + 1
= 36a² – 120a + 101

Question 5.
If f(x) = \(\frac{1}{x}\), g(x) = √x for all x ∈ (0, ∞) then find (g o f) (x).
Solution:
f(x) = \(\frac{1}{x}\), g(x) = √x, ∀ x ∈ (0, ∞)
(g o f) (x) = g(f(x))
= g(\(\frac{1}{x}\)) [∵ f(x) = \(\frac{1}{x}\)]
= \(\sqrt{\frac{1}{x}}\)
= \(\frac{1}{\sqrt{x}}\) [∵ g(x) = √x]
∴ (gof) (x) = \(\frac{1}{\sqrt{x}}\)

Question 6.
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) for all x ∈ R, find (g o f) (x).
Solution:
f(x) = 2x – 1, g(x) = \(\frac{x+1}{2}\) ∀ x ∈ R
(g o f) (x) = g(f(x))
= g(2x – 1) [∵ f(x) = 2x – 1]
= \(\frac{(2 x-1)+1}{2}\)
= x [∵ g(x) = \(\frac{x+1}{2}\)]
∴ (g o f) (x) = x

Question 7.
If f(x) = 2, g(x) = x², h(x) = 2x for all x ∈ R, then find (f o (g o h)) (x).
Solution:
f(x) = 2, g(x) = x², h(x) = 2x, ∀ x ∈ R
[f o (g o h) (x)]
= [f o g (h(x))]
= f o g (2x) [∵ h(x) = 2x]
= f[g(2x)]
= f((2x)²) [∵ g(x) = x²]
= f(4x²) = 2 [∵ f(x) = 2]
∴ [f o (g o h) (x)] = 2

Question 8.
Find the inverse of the following functions.
(i) a, b ∈ R, f : R → R defined by f(x) = ax + b, (a ≠ 0).
Solution:
a, b ∈ R, f : R → R and f(x) = ax + b, a ≠ 0
Let y = f(x) = ax + b
⇒ y = f(x)
⇒ x = f^-1(y) ……..(i)
and y = ax + b
⇒ x = \(\frac{y-b}{a}\) ……..(ii)
From (i) and (ii)
f^-1(y) = \(\frac{y-b}{a}\)
⇒ f^-1(x) = \(\frac{x-b}{a}\)

(ii) f : R → (0, ∞) defined by f(x) = 5^x
Solution:
f : R → (0, ∞) and f(x) = 5^x
Let y = f (x) = 5^x
y = f(x) ⇒ x = f^-1(y) ……(i)
and y = 5^x ⇒ log₅ (y) = x ……..(ii)
From (i) and (ii)
f^-1(y) = log₅(y) ⇒ f^-1(x) = log5 (x)

(iii) f : (0, ∞) → R defined by f(x) = log₂ (x).
Solution:
f : (0, ∞) → R and f(x) = log₂ (x)
Let y = f(x) = log₂ (x)
∵ y = f(x) ⇒ x = f^-1(y) ……..(i)
and y = log₂(x) ⇒ x = 2y
From (i) and (ii)
f^-1(y) = 2y ⇒ f^-1(x) = 2x

Question 9.
If f(x) = 1 + x + x² + …… for |x| < 1 then show that f^-1(x) = \(\frac{x-1}{x}\)
Solution:
f(x) = 1 + x + x² + ……..

Question 10.
If f : [1, ∞) ⇒ [1, ∞) defined by f(x) = \(2^{x(x-1)}\) then find f^-1(x).
Solution:

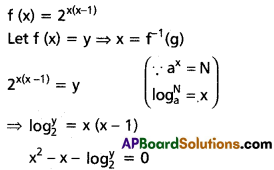
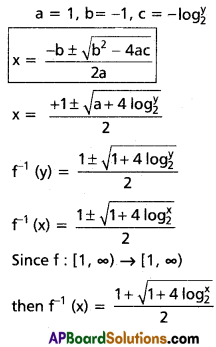
II.

Question 1.
If f(x) = \(\frac{x-1}{x+1}\), x ≠ ±1, then verify (f o f^-1) (x) = x.
Solution:
Given f(x) = \(\frac{x-1}{x+1}\), x ≠ ±1
Let y = f(x) = \(\frac{x-1}{x+1}\)
∵ y = f(x) ⇒ x = f^-1(y) ……(i)
and y = \(\frac{x-1}{x+1}\)

Question 2.
If A = {1, 2, 3}, B = {α, β, γ}, C = {p, q, r} and f : A → B, g : B → C are defined by f = {(1, α), (2, γ), (3, β)}, g = {(α, q), (β, r), (γ, p)}, then show that f and g are bijective functions and (gof)^-1 = f^-1 o g^-1.
Solution:
A = {1, 2, 3}, B = {α, β, γ},
f : A → B and f = {(1, α), (2, γ), (3, β)}
⇒ f(1) = α, f(2) = γ, f(3) = β
∵ Distinct elements of A have distinct f – images in B, f: A → B is an injective function.
Range of f = {α, γ, β} = B(co-domain)
∴ f : A → B is a surjective function.
Hence f : A → B is a bijective function.
B = {α, β, γ}, C = {p, q, r}, g : B → C and g : {(α, q), (β, r), (γ, p)}
⇒ g(α) = q, g(β) = r, g(γ) = p
∴ Distinct elements of B have distinct g – images in C, g : B → C is an injective function.
Range of g = {q, r, p} = C, (co-domain)
∴ g : B → C is a surjective function
Hence g : B → C is a bijective function
Now f = {(1, α), (2, γ), (3, β)}
g = {(α, q), (β, r), (γ, p)}
g o f = {(1, q), (2, p), (3, r)}
∴ (g o f)^-1 = {(q, 1), (r, 3), (p, 2)} ………(1)
g^-1 = {(q, α), (r, β), (p, γ)}
f^-1 = {(α, 1), (γ, 2),(β, 3)}
Now f^-1 o g^-1 = {(q, 1), (r, 3), (p, 2)} …….(2)
From eq’s (1) and (2)
(gof)^-1 = f^-1 o g^-1

Question 3.
If f : R → R, g : R → R defined by f(x) = 3x – 2, g(x) = x² + 1, then find
(i) (g o f^-1) (2)
(ii) (g o f)(x – 1)
Solution:
f : R → R, g : R → R and f(x) = 3x – 2
f is a bijective function ⇒ its inverse exists
Let y = f(x) = 3x – 2
∵ y = f(x) ⇒ x = f^-1(y) …….(i)
and y = 3x – 2
⇒ x = \(\frac{y+2}{3}\) ……..(ii)
From (i) and (ii)
f^-1(y) = \(\frac{y+2}{3}\)
⇒ f^-1(x) = \(\frac{x+2}{3}\)
Now (gof^-1) (2)
= g(f^-1(2))

∴ (g o f^-1) (2) = \(\frac{25}{9}\)

(ii) (g o f) (x -1)
= g(f(x – 1))
= g(3(x – 1) – 2) [∵ f(x) = 3x – 2]
= g(3x – 5)
= (3x – 5)² + 1 [∵ g(x) = x² + 1]
= 9x² – 30x + 26
∴ (g o f) (x – 1) = 9x² – 30x + 26

Question 4.
Let f = {(1, a), (2, c), (4, d), (3, b)} and g^-1 = {(2, a), (4, b), (1, c), (3, d)} then show that (gof)^-1 = f^-1 o g^-1
Solution:
f = {(1, a), (2, c), (4, d), (3, b)}
∴ f^-1 = {(a, 1), (c, 2), (d, 4), (b, 3)}
g^-1 = {(2, a), (4, b), (1, c), (3, d)}
∴ g = {(a, 2), (b, 4), (c, 1), (d, 3)}
(g o f) = {(1, 2), (2, 1), (4, 3), (3, 4)}
∴ (gof)^-1 = {(2, 1), (1, 2), (3, 4), (4, 3)} ……….(1)
f^-1 o g^-1 = {(2, 1), (4, 3), (1, 2), (3, 4)} ……..(2)
From eq’s (1) and (2), we observe (gof)^-1 = f^-1 o g^-1

Question 5.
Let f : R → R, g : R → R be defined by f(x) = 2x – 3, g(x) = x³ + 5 then find (f o g)^-1 (x).
Solution:
f : R → R, g : R → R and f(x) = 2x – 3 and g(x) = x³ + 5
Now (fog) (x) = f(g(x))
= f(x³ + 5) [∵ g(x) = x² + 5]
= 2(x³ + 5) – 3 [∵ f(x) = 2x – 3]
= 2x³ + 7
∴ (f o g) (x) = 2x³ + 7
Let y = (f o g) (x) = 2x³ + 7
∵ y = (fog)(x)
⇒ x = (fog)^-1 (y) …….(1)
and y = 2x³ + 7
⇒ x³ = \(\frac{y-7}{2}\)
⇒ x = \(\left(\frac{y-7}{2}\right)^{\frac{1}{3}}\) …..(2)
From eq’s (1) and (2),
(f o g)^-1 (y) = \(\left(\frac{y-7}{2}\right)^{\frac{1}{3}}\)
∴ (f o g)^-1 (x) = \(\left(\frac{x-7}{2}\right)^{\frac{1}{3}}\)

Question 6.
Let f(x) = x², g(x) = 2^x. Then solve the equation (f o g) (x) = (g o f) (x)
Solution:
Given f(x) = x² and g(x) = 2^x
Now (f o g) (x) = f(g(x))
= f(2^x) [∵ g(x) = 2^x]
= (2^x)²
= 2^2x [∵ f(x) = x²]
∴ (f o g) (x) = 2^2x ……(1)
and (g o f) (x) = g(f(x))
= g(x²) [∵ f(x) = x²]
= \((2)^{x^{2}}\) [∵ g(x) = 2^x]
∴ (g o f) (x) = \((2)^{x^{2}}\)
∵ (f o g) (x) = (g o f) (x)
⇒ 2^2x = \((2)^{x^{2}}\)
⇒ 2^x = x²
⇒ x² – 2x = 0
⇒ x(x – 2) = 0
⇒ x = 0, x = 2
∴ x = 0, 2

Question 7.
If f(x) = \(\frac{x+1}{x-1}\), (x ≠ ±1) then find (fofof) (x) and (fofofof) (x).
Solution:
f(x) = \(\frac{x+1}{x-1}\), (x ≠ ±1)
(i) (fofof) (x) = (fof) [f(x)]
= (fof) \(\left(\frac{x+1}{x-1}\right)\) [∵ f(x) = \(\left(\frac{x+1}{x-1}\right)\)]

(ii) (fofofof) (x) = f[(f o f o f) (x)]
= f [f(x)] {from (1)}

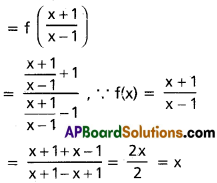
In the above problem if a number of f is even its answer is x and if a number of f is odd its answer is f(x).