Inter 1st Year Maths 1A Hyperbolic Functions Important Questions

Students get through Maths 1A Important Questions Inter 1st Year Maths 1A Hyperbolic Functions Important Questions which are most likely to be asked in the exam.

Intermediate 1st Year Maths 1A Hyperbolic Functions Important Questions

Question 1.
Prove that for any x ∈ R, sinh (3x) = 3 sinh x + 4sinh x
Answer:
LHS = sinh (3x)
= sinh (2x + x)
= sinh (2x) . cosh(x) + cosh (2x) . sinh (x) = (2sinh x cosh x)cosh x (1 +2sinh² x)sinh x
= 2 sinh x (cosh² x) + (1 + 2 sinh² x) sinh x
= 2 sinh x (1 + sinh² x) + (1 + 2 sinh² x) sinh x
∵ cosh² x – sinh² x = 1
= 3 sinh x + 4 sinh³ x
∴ sinh (3x) = 3 sinh x + 4 sinh³ x

Question 2.
Prove that for any x ∈ R, tanh 3x = \(\frac{3 \tanh x+\tanh ^{3} x}{1+3 \tanh ^{2} x}\)
Answer:
tanh 3x = tan (2x + x)

Question 3.
If cosh x = \(\frac{5}{2}\), find the values of
i) cosh (2x) and
ii) sinh (2x)
Answer:
cosh (x) = \(\frac{5}{2}\)
(i) cosh (2x) = 2 cosh² (x) – 1
= 2(\(\frac{5}{2}\))² – 1 = \(\frac{25}{2}\) – 1 = \(\frac{23}{2}\)

ii) sinh² (2x) = cosh² (2x) – 1
= (\(\frac{23}{2}\))² – 1 = \(\frac{529-4}{2}\) = \(\frac{525}{4}\)
∴ sinh (2x) = ±\(\sqrt{\frac{525}{4}}\) = ±\(\frac{5 \sqrt{21}}{2}\)

Question 4.
If coshx = sec θ then prove that tan h²\(\frac{x}{2}\) = tan²\(\frac{\theta}{2}\)
Answer:
tan h²\(\frac{x}{2}\) = \(\frac{\cosh x-1}{\cosh x+1}\)
= \(\frac{\sec \theta-1}{\sec \theta+1}\) = \(\frac{1-\cos \theta}{1+\cos \theta}\) = tan²\(\frac{\theta}{2}\)

Question 5.
If θ ∈ (-\(\frac{\pi}{4}\), \(\frac{\pi}{4}\)) and x = log_e(cot(\(\frac{\pi}{4}\) + θ) then prove that
i) cosh x = sec 2θ and
ii) sinh x = -tan 2θ
Answer:

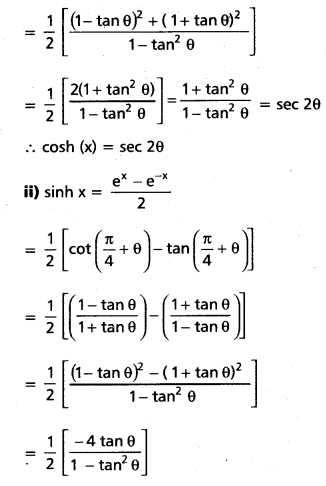
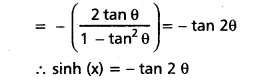
Question 6.
If sinh x = 5, show that x = log_e (5 + \(\sqrt{26}\))
Answer:
∴ sinh (x) = 5
⇒ x = sinh^-1 (5)
= log_e (5 + \(\sqrt{5^{2}+1}\))
= log_e (5 + \(\sqrt{26}\))
[sin^-1 (x) = log_e (x + \(\sqrt{x^{2}+1}\)) for all x ∈ R]

Question 7.
Show that tanh^-1(\(\frac{1}{2}\)) = \(\frac{1}{2}\) log_e3 (A.P) [Mar 15; May 07, 05; Mar 08, 05]
Answer:
∵tanh^-1 (x) = \(\frac{1}{2}\)log_e(\(\frac{1+x}{1-x}\)) for all x ∈ (-1, 1)
∵ tanh^-1 (\(\frac{1}{2}\)) = \(\frac{1}{2}\)log_e(\(\frac{1+\frac{1}{2}}{1-\frac{1}{2}}\))
= \(\frac{1}{2}\)log_e(3)