Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Matrices Solutions Exercise 3(g) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Matrices Solutions Exercise 3(g)
Examine whether the following systems of equations are consistent or inconsistent and if consistent find the complete solutions.
Question 1.
x + y + z = 4
2x + 5y – 2z = 3
x + 7y – 7z = 5
Solution:

ρ(A) = 2, ρ(AB) = 3
ρ(A) ≠ ρ(AB)
∴ The given system of equations are in consistent.
![]()
Question 2.
x + y + z = 6
x – y + z = 2
2x – y + 3z = 9
Solution:


Question 3.
x + y + z = 1
2x + y + z = 2
x + 2y + 2z = 1
Solution:
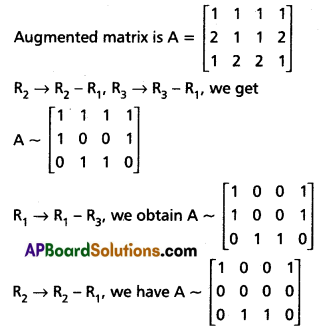
ρ(A) = 2 = ρ(AB) < 3
The given system of equations are consistent and have infinitely many solutions.
The solutions are given by [(x, y, z) 1x = 1, y + z = 0].
Question 4.
x + y + z = 9
2x + 5y + 7z = 52
2x + y – z = 0
Solution:

∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent have a unique solution.
∴ Solution is given by x = 1, y = 3, z = 5.
![]()
Question 5.
x + y + z = 6
x + 2y + 3z = 10
x + 2y + 4z = 1
Solution:
Augmented matrix A = \(\left[\begin{array}{cccc}
1 & 1 & 1 & 6 \\
1 & 2 & 3 & 10 \\
1 & 2 & 4 & 1
\end{array}\right]\)
By R2 → R2 – R1, R3 → R3 – R2, we obtain

∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent.
They have a unique solution.
∴ Solution is given by x = -7, y = 22, z = -9.
Question 6.
x – 3y – 8z = -10
3x + y – 4z = 0
2x + 5y + 6z = 13
Solution:
The Augmented matrix
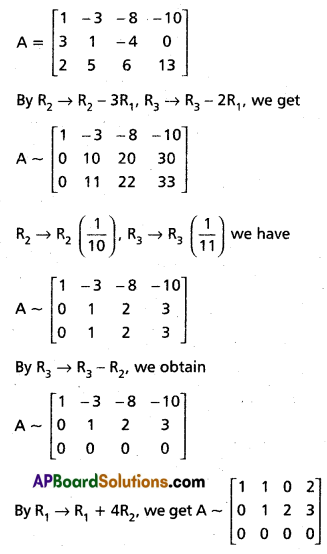
ρ(A) = ρ(AB) = 2 < 3
∴ The given system of equations are consistent have infinitely many solutions.
x + y = 2 and y + 2z = 3
Taking z = k, y = 3 – 2z = 3-2k
x = 2 – y
= 2 – (3 – 2k)
= 2 – 3 + 2k
= 2k – 1
∴ The solutions are given by x = -1 + 2k, y = 3 – 2k, z = k where ‘k’ is any scalar.
Question 7.
2x + 3y + z = 9
x + 2y + 3z = 6
3x + y + 2z = 8
Solution:

∴ ρ(A) = ρ(AB) = 3
The given system of equations are consistent have a unique solution.
∴ Solution is given by x = \(\frac{35}{18}\), y = \(\frac{29}{18}\), z = \(\frac{5}{18}\)
![]()
Question 8.
x + y + 4z = 6
3x + 2y – 2z = 9
5x + y + 2z = 13
Solution:

∴ ρ(A) = ρ(AB) = 3
∴ The given system of equations are consistent have a unique solution.
∴ Solution is given by x = 2, y = 2, z = \(\frac{1}{2}\)