Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(b) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(b)
I. Find the periods for the given 1 – 5 functions.
Question 1.
cos(3x + 5) + 7
Solution:
f(x) = cos(3x + 5) + 7
We know that the function g(x) = cos x for all x ∈ R has the period 2π.
Now f(x) = cos(3x + 5) + 7
We get that f(x) is periodic and the period of f is \(\frac{2 \pi}{|3|}=\frac{2 \pi}{3}\)
Question 2.
tan 5x
Solution:
The function g(x) = tan x periodic and π is the period.
∴ f(x) = tan 5x periodic and its period is \(\frac{\pi}{|5|}=\frac{\pi}{5}\)
![]()
Question 3.
\(\cos \left(\frac{4 x+9}{5}\right)\)
Solution:
The function h(x) = cos x for all x ∈ R has the period 2π.
Now f(x) = \(\cos \left(\frac{4 x}{5}+\frac{9}{5}\right)\) is periodic and period of f is \(\frac{2 \pi}{\left(\frac{4}{5}\right)}=\frac{5 \pi}{2}\)
Question 4.
|sin x|
Solution:
The function h(x) = sin x for all x ∈ R has the period 2π.
But f(x) = |sin x| is periodic and its period is π.
∵ f(x + π) = |sin(x + π)|
= |-sin x|
= sin x
Question 5.
tan(x + 4x + 9x + …… + n2x) (n any positive integer)
Solution:
tan(12 + 22 + 32 + …… + n2) x = \(\tan \left[\frac{n(n+1)(2 n+1)}{6}\right] x\)
period = \(\frac{6 \pi}{n(n+1)(2 n+1)}\)
Question 6.
Find a sine function whose period is \(\frac{2}{3}\)
Solution:
\(\frac{2 \pi}{|k|}=\frac{2}{3}\)
3π = |k|
∴ sin kx = sin 3πx
![]()
Question 7.
Find a cosine function whose period is 7.
Solution:
\(\frac{2 \pi}{|k|}\) = 7
\(\frac{2 \pi}{7}\) = |k|
∴ cos kx = cos \(\frac{2 \pi}{7}\) x
II. Sketch the graph of the following functions.
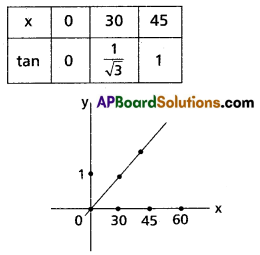
Question 1.
tan x between 0 and \(\frac{\pi}{4}\)
Solution:
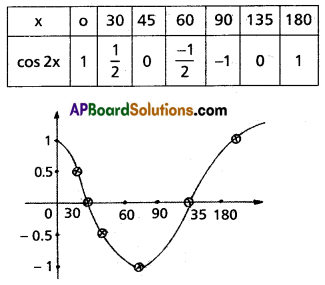
Question 2.
cos 2x in [0, π]
Solution:
Question 3.
sin 2x in the interval (0, π)
Solution:
![]()
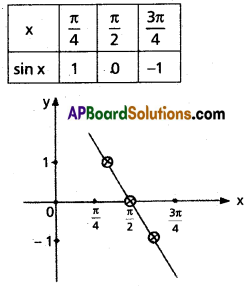
Question 4.
sin x in the interval [-π, +π]
Solution:
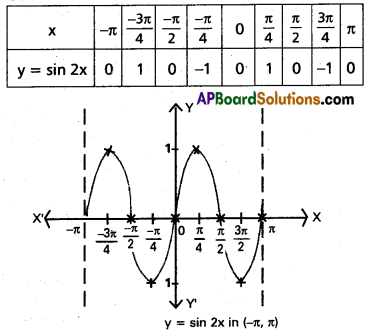
Question 5.
cos2x in [0, π]
Solution:
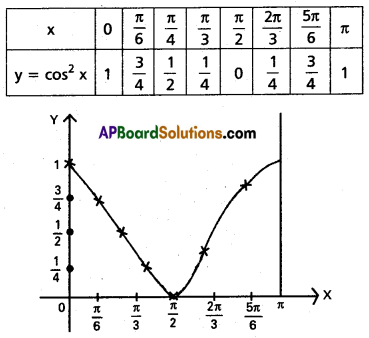
III.
Question 1.
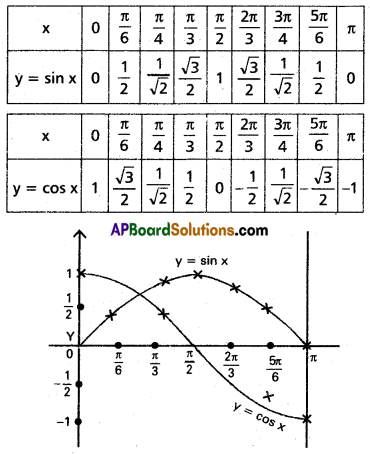
Sketch the region enclosed by y = sin x, y = cos x and X-axis in the interval [0, π].
Solution: