Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Ex 6(c)

Practicing the Intermediate 1st Year Maths 1A Textbook Solutions Inter 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1A Trigonometric Ratios up to Transformations Solutions Exercise 6(c)

I.

Question 1.
Simplify the following.
(i) cos 100° cos 40° + sin 100° sin 40°
Solution:
cos 100° cos 40° + sin 100° sin 40° = cos(100° – 40°)
= cos 60°
= \(\frac{1}{2}\)

(ii) \(\frac{\cot 55 \cot 35}{\cot 55+\cot 35}\)
Solution:
\(\frac{\cot 55 \cot 35}{\cot 55+\cot 35}\) = cot(55 + 35)
= cot 90
= 0

(iii) \(\tan \left[\frac{\pi}{4}+\theta\right] \cdot \tan \left[\frac{\pi}{4}-\theta\right]\)
Solution:
\(\tan \left[\frac{\pi}{4}+\theta\right] \cdot \tan \left[\frac{\pi}{4}-\theta\right]\)
\(\left[\frac{1+\tan A}{1-\tan A}\right]\left[\frac{1-\tan A}{1+\tan A}\right]\) = 1

(iv) tan 75° + cot 75°
Solution:
tan 75° + cot 75°
= 2 + √3 + 2 – √3
= 4

(v) sin 1140° cos 390° – cos 780° sin 750°
Solution:
sin 1140° cos 390° – cos 780° sin 750°
= sin(3 × 360° + 60°) cos(360°+ 30°) – cos(2 × 360° + 60°) sin(2 × 360° + 30)
= sin 60° cos 30° – cos 60° sin 30°
= sin(60° – 30°)
= sin 30°
= \(\frac{1}{2}\)

Question 2.
(i) Express \(\frac{\sqrt{3} \cos 25+\sin 25}{2}\) as a sine of an angle.
Solution:
\(\frac{\sqrt{3} \cos 25+\sin 25}{2}\)
= \(\frac{\sqrt{3}}{2}\) cos 25° + \(\frac{1}{2}\) sin 25°
= sin 60° cos 25° + cos 60° sin 25°
= sin (60° + 25°)
= sin 85°

(ii) Express (cos θ – sin θ) as a cosine of an angle.
Solution:
cos θ – sin θ
Divide & multiply with √2
\(\frac{1}{\sqrt{2}}\) √2 (cos θ – sin θ)
= √2 \(\frac{1}{\sqrt{2}}\) cos θ – sin θ \(\frac{1}{\sqrt{2}}\)
= √2 [cos \(\frac{\pi}{4}\) cos θ – sin \(\frac{\pi}{4}\) sin θ]
= √2 \(\cos \left[\frac{\pi}{4}+\theta\right]\)

(iii) Express tan θ in terms of tan α, If sin (θ + α) = cos (θ + α).
Solution:
tan θ in term of tan α, if sin(θ + α) = cos (θ + α)
given sin(θ + α) = cos(θ + α)
sin θ cos α + cos θ sin α = cos θ cos α – sin θ sin α and cos θ cos α
\(\frac{\sin \theta \cos \alpha}{\cos \theta \cos \alpha}+\frac{\cos \theta \sin \alpha}{\cos \theta \cos \alpha}=\frac{\cos \theta \cos \alpha}{\cos \theta \cos \alpha}\) – \(\frac{\sin \theta \sin \alpha}{\cos \theta \cos \alpha}\)
tan θ + tan α = 1 – tan θ tan α
tan θ + tan θ tan α = 1 – tan α
tan θ (1 + tan α) = 1 – tan α
tan θ = \(\frac{1-\tan \alpha}{1+\tan \alpha}\)

Question 3.
(i) If tan θ = \(\frac{\cos 11^{\circ}+\sin 11^{\circ}}{\cos 11^{\circ}-\sin 11^{\circ}}\) and θ is the third quadrant find θ.
Solution:
Given tan θ = \(\frac{\cos 11^{\circ}+\sin 11^{\circ}}{\cos 11^{\circ}-\sin 11^{\circ}}\)
= \(\frac{1+\tan 11^{\circ}}{1-\tan 11^{\circ}}\)
= tan (45° + 11°)
= tan (56°)
tan θ = tan 56° = tan (180° + 50°) = tan 236°
∴ θ = 236°

(ii) If 0° < A, B < 90°, such that cos A = \(\frac{5}{13}\) and sin B = \(\frac{4}{5}\), find the value of sin(A – B).
Solution:

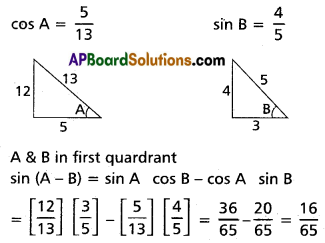
(iii) What is the value of tan 20° + tan 40° + √3 tan 20° tan 40°?
Solution:
consider 20° + 40° = 60°
tan (20° + 40°) = tan 60°
\(\frac{\tan 20^{\circ}+\tan 40^{\circ}}{1-\tan 20^{\circ} \tan 40^{\circ}}\) = √3
tan 20° + tan 40° = √3 – √3 tan 20° tan 40°
tan 20° + tan 40° + √3 tan 20° tan 40° = √3

(iv) Find the value of tan 56° – tan 11° – tan 56° tan 11°.
Solution:
consider 56° – 11° = 45°
tan (56° – 11) = tan 45°
\(\frac{\tan 56^{\circ}-\tan 11^{\circ}}{1+\tan 56^{\circ} \tan 11^{\circ}}\) = 1
tan 56° – tan 11 ° = 1 + tan 56° tan 11°
tan 56° – tan 11° – tan 56° tan 11° = 1

(v) Evaluate \(\sum \frac{\sin (A+B) \sin (A-B)}{\cos ^{2} A \cos ^{2} B}\); if none of cos A, cos B, cos C is zero.
Solution:

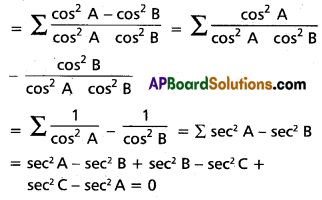
(vi) Evaluate \(\sum \frac{\sin (C-A)}{\sin C \sin A}\) if none of sin A, sin B, sin C is zero.
Solution:

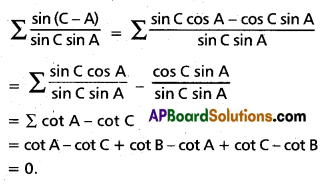
Question 4.
Prove that
(i) cos 35° + cos 85° + cos 155° = 0
Solution:
cos 35° + cos 85° + cos 155°
= -cos 85° + 2 cos\(\left(\frac{35+155}{2}\right)\) cos\(\left(\frac{35-155}{2}\right)\)
= -cos 85° + 2 cos 85° \(\left(\frac{1}{2}\right)\)
= -cos 85° + cos 85°
= 0

(ii) tan 72° = tan 18° + 2 tan 54°
Solution:
cos A – tan A = \(\frac{1}{\tan A}\) – tan A
= \(\frac{1-\tan ^{2} A}{\tan A}\)
= \(\frac{2\left(1-\tan ^{2} A\right)}{2 \tan A}\)
= \(\frac{2}{\tan 2 A}\)
= 2 cot 2A
cot A = tan A + 2 cot 2A
put A = 18
cot 18° = tan 18° + 2 cot 36°
cot (90° – 72°) = tan 18° + 2 cot (90° – 54°)
tan 72° = tan 18° + 2 tan 54°

(iii) sin 750° cos 480° + cos 120° cos 60° = \(\frac{-1}{2}\)
Solution:
sin 750° = sin (2 × 360° + 30°)
= sin 30°
= \(\frac{1}{2}\)
cos 480° = cos (360° + 120°)
= cos 120°
= \(\frac{-1}{2}\)
L.H.S. = sin 750° cos 480° + cos 120° cos 60°
= \(\frac{1}{2}\left(\frac{-1}{2}\right)+\left(\frac{-1}{2}\right)\left(\frac{1}{2}\right)\)
= \(\frac{-1}{4}-\frac{1}{4}\)
= \(\frac{-1}{2}\)

(iv) cos A + cos(\(\frac{4 \pi}{3}\) – A) + cos(\(\frac{4 \pi}{3}\) + A) = o
Solution:
cos A + cos(\(\frac{4 \pi}{3}\) – A) + cos(\(\frac{4 \pi}{3}\) + A)
= cos A + 2 cos \(\frac{4 \pi}{3}\) cos A (∵ cos(A + B) + cos(A – B) = 2 cos A cos B)
= cos A + 2\(\left(\frac{-1}{2}\right)\) cos A
= cos A – cos A
= 0

(v) cos²θ + cos²(\(\frac{2 \pi}{3}\) + θ) + cos²(\(\frac{2 \pi}{3}\) – θ)
Solution:

Question 5.
Evaluate
(i) \(\sin ^{2} 82 \frac{1}{2}^{\circ}-\sin ^{2} 22 \frac{1^{\circ}}{2}\)
Solution:

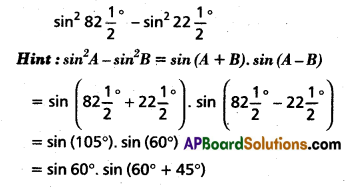
(ii) \(\cos ^{2} 112 \frac{1}{2}^{\circ}-\sin ^{2} 52 \frac{1}{2}^{\circ}\)
Solution:

(iii) \(\sin ^{2}\left[\frac{\pi}{8}+\frac{A}{2}\right]-\sin ^{2}\left[\frac{\pi}{8}-\frac{A}{2}\right]\)
Solution:

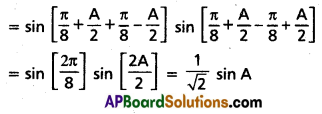
(iv) \(\cos ^{2} 52 \frac{1}{2}^{\circ}-\sin ^{2} 22 \frac{1}{2}^{\circ}\)
Solution:

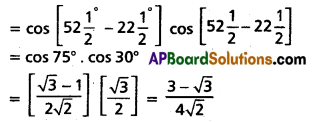
Question 6.
Find the minimum and maximum values of
(i) 3 cos x + 4 sin x
Solution:
a = 4, b = 3, c = 0
Minimum value = \(c-\sqrt{a^{2}+b^{2}}=\sqrt{16+9}=-5\)
Maximum value = \(c+\sqrt{a^{2}+b^{2}}=\sqrt{16+9}=5\)

(ii) sin 2x – cos 2x
Solution:
a = 1, b = -1, c = 0
minimum value = \(c-\sqrt{a^{2}+b^{2}}=-\sqrt{1+1}\) = -√2
maximum value = \(c+\sqrt{a^{2}+b^{2}}=\sqrt{1+1}=\sqrt{2}\)

Question 7.
Find the range of
(i) 7 cos x – 24 sin x + 5
Solution:

(ii) 13 cos x + 3√3 sin x – 4
Solution:

II.

Question 1.
(i) If cos α = \(\frac{-3}{5}\) and sin β = \(\frac{7}{25}\), where \(\frac{\pi}{2}\) < α < π and 0 < β < \(\frac{\pi}{2}\), then find the values of tan(α + β) and sin(α + β).
Solution:

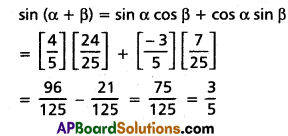
(ii) If 0 < A < B < \(\frac{\pi}{4}\) and sin (A + B) = \(\frac{24}{25}\) and cos (A – B) = \(\frac{4}{5}\), then find the value of tan 2A.
Solution:

(iii) If A + B, A are acute angles such that sin (A + B) = \(\frac{24}{25}\) and tan A = \(\frac{3}{4}\), then find the value of cos B.
Solution:
sin (A + B) = \(\frac{24}{25}\) and (A + B) is acute angle

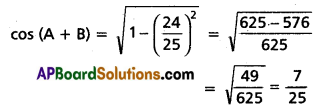
(iv) If tan α – tan β = m and cot α – cot β = n, then prove that cot (α – β) = \(\frac{1}{m}-\frac{1}{n}\)
Solution:

(v) If tan (α – β) = \(\frac{7}{24}\) and tan α = \(\frac{4}{3}\), where α and β are in the first quadrant prove that α – β = \(\frac{\pi}{2}\).
Solution:

Question 2.
(i) Find the expansion of sin (A + B – C).
Solution:
sin (A + B – C) = sin [(A + B) – C]
= sin (A + B). cos C – cos (A + B) sin C
= (sin A cos B + cos A sin B) cos C – (cos A cos B – sin A sin B) sin C
= sin A cos B cos C + cos A sin B cos C – cos A cos B sin C + sin A sin B sin C

(ii) Find the expansion of cos (A – B – C).
Solution:
cos (A – B – C) = cos {(A – B) – C}
= cos (A – B) cos C + sin (A – B) sin C
= (cos A cos B + sin A sin B) cos C + (sin A cos B – cos A sin B) sin C
= cos A cos B cos C + sin A sin B cos C + sin A cos B sin C – cos A sin B sin C

(iii) In a ΔABC, A is obtuse. If sin A = \(\frac{3}{5}\) and sin B = \(\frac{5}{13}\), then show that sin C = \(\frac{16}{65}\)
Solution:
Given sin A = \(\frac{3}{5}\)
cos²A = 1 – sin²A
= 1 – \(\frac{9}{25}\)
= \(\frac{16}{25}\)
cos A = ±\(\frac{4}{5}\)
A is obtuse ⇒ 90° < A < 180°
A tan in II quadrant ⇒ cos A is negative
∴ cos A = \(\frac{-4}{5}\),
Given sin β = \(\frac{5}{13}\)
cos²β = 1 – sin²β
= 1 – \(\frac{25}{169}\)
= \(\frac{144}{169}\)
cos β = ±\(\frac{5}{13}\)
β is acute ⇒ cos β is possible
sin β = \(\frac{12}{13}\)
A + B + C = 180°
C = 180° – (A + B)
sin C = sin (180° – (A + B))
= sin (A + B)
= sin A cos B + cos A sin B
= \(\left(\frac{3}{5}\right)\left(\frac{12}{13}\right)+\left(\frac{-4}{5}\right)\left(\frac{5}{13}\right)\)
= \(\frac{36-20}{65}\)
= \(\frac{16}{65}\)
∴ sin C = \(\frac{16}{65}\)

(iv) If \(\frac{\sin (\alpha+\beta)}{\sin (\alpha-\beta)}=\frac{a+b}{a-b}\), then prove that tan β = ab tan α
Solution:

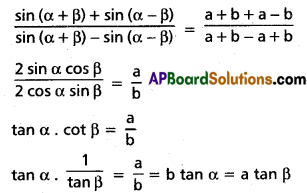
III.

Question 1.
(i) If A – B = \(\frac{3 \pi}{4}\), then show that (1 – tan A) (1 + tan B) = 2.
Solution:
A – B = \(\frac{3 \pi}{4}\)
tan (A – B) = tan \(\frac{3 \pi}{4}\)
\(\frac{\tan A-\tan B}{1+\tan A \tan B}\) = -1
tan A – tan B = -1 – tan A tan B
1 = -tan A + tan B – tan A tan B
2 = 1 – tan A + tan B – tan A tan B
2 = (1 – tan A) – tan B (1 – tan A)
(1 – tan A) (1 – tan B) = 2

(ii) If A + B + C = \(\frac{\pi}{2}\) and none of A, B, C is an odd multiple of \(\frac{\pi}{2}\), then prove that
(a) cot A + cot B + cot C = cot A cot B cot C
(b) tan A tan B + tan B tan C + tan C tan A = 1 and hence, show that \(\sum \frac{\cos (B+C)}{\cos B \cos C}\) = 2
Solution:

Question 2.
(i) Prove that sin²α + cos²(α + β) + 2 sin α sin β cos(α + β) is independent of α.
Solution:
sin²α + cos²(α + β) + 2 sin α cos (α + β)
= sin²α + cos(α + β) (cos(α + β) + 2 sin α sin β)
= sin²α + cos(α + β) (cos α cos β – sin α sin β + 2 sin α sin β)
= sin²α + cos(α + β) (cos α cos β + sin α sin β)
= sin²α + cos(α + β) cos(α – β)
= sin²α + cos²β – sin²α
= cos²β

(ii) Prove that cos²(α – β) + cos²β – 2 cos(α – β) cos α cos β is independent of β.
Solution:
cos²(α – β) + cos²β – 2 cos (α – β) cos α cos β
= cos²(α – β) + cos²β – cos (α – β) [cos (α + β) + cos (α – β)]
= cos²(α – β) + cos²β – cos (α – β) cos (α + β) – cos²(α – β)
= cos²β – [cos²β – sin²α]
= cos²β – cos²β + sin²α
= sin²α