Inter 1st Year Maths 1B Applications of Derivatives Solutions Ex 10(g)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(g) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Applications of Derivatives Solutions Exercise 10(g)

I.

Question 1.
Without using the derivative, show that
i) The function f(x) = 3x + 7 is strictly increasing on R.
Solution:
Let x₁, x₂ ∈ R with x₁ < x₂
Then 3x₁ < 3x₂
Adding 7 on both sides
3x₁ + 7 < 3x₂ + 7
⇒ f(x₁) < f(x₂)
∴ x₁ < x₂ ⇒ f(x₁) < f(x₂) ∀ x₁ x₂ ∈ R
∴ The given function is strictly increasing on R

ii) The function f(x) = (\(\frac{1}{2}\))^x is strictly decreasing on R.
Solution:
f(x) = (\(\frac{1}{2}\))^x
Let x₁, x₂ ∈ R
Such that x₁ < x₂
⇒ (\(\frac{1}{2}\))^x₁ > (\(\frac{1}{2}\))^x₂
⇒ f(x₁) > f(x₂)
∴ f(x) is strictly decreasing on R.

iii) The function f(x) = e^3x is strictly increasing on R.
Solution:
f(x) = e^3x
Let x₁, x₂ ∈ R such that x₁ < x₂
We know that of a > b then e^a > e^b
Then e^3x < e^3x₂
⇒ f(x₁) < f(x₂)
∴ f is strictly increasing on R.

iv) The function f(x) = 5. – 7x is strictly decreasing on R.
Solution:
f(x) = 5 – 7x
Let x₁ x₂ ∈ R
Such that x₁ < x₂
Then 7x₁ < 7x₂
-7x₁ > -7x₂
Adding 5 on bothsides
5 – 7x₁ > 5 – 7x₂
f(x₁) > (x₂)
∴ x₁ < x₂ ⇒ f(x₁) > f(x₂) V x₁ x₂ ∈ R.
The given function f is strictly decreasing on R.

Question 2.
Show that the function f(x) = sin x. Define on R is neither increasing nor decreasing on (0, π).
Solution:
f(x) = sin x
Since 0 < x < n
Consider 0 < x
f(0) < f(x)
sin 0 < sin x
0 < sin x ……….. (1)
Consider x < n
f(x) < f(π)
sin x < sin π 0 > sin x ………….. (2)
From (1) & (2); f(x) is neither increasing nor decreasing.

II.

Question 1.
Find the intervals in which the following functions are strictly increasing or strictly decreasing.
i) x² + 2x – 5
Solution:
Let f(x) = x² + 2x – 5
f'(x) = 2x + 2
f(x) is increasing if f'(x) > 0
⇒ 2x + 2 < 0 ⇒ x+ 1 > 0
x > -1
f(x) is increasing If x ∈ (-1, ∞)
f(x) is decreasing If f'(x) < 0
⇒ 2x + 2 < 0
⇒ x + 1 < 0
⇒ x < -1 f(x) is decreasing if x ∈ (-∞, -1).

ii) 6 – 9x – x².
Solution:
Let f(x) = 6 – 9x – x²
f'(x) = -9 – 2x
f(x) is increasing if f'(x) > 0
⇒ -9 -2x > 0
⇒ 2x + 9 < 0
x < \(\frac{-9}{2}\)
f(x) is increasing if x ∈ (-∞, \(\frac{-9}{2}\))
f(x) is decreasing if f'(x) < 0
⇒ 2x + 9 > 0
⇒ x > \(\frac{-9}{2}\)
f(x) is decreasing of x ∈ (\(\frac{-9}{2}\), ∞)

iii) (x + 1)³ (x – 1)³.
Solution:
Let f(x) = (x + 1)³ (x – 1)³
= (x² – 1)³
x⁶ – 1 – 3x⁴ + 3x ²
f'(x) = 6x⁵ – 12x³ + 6x
= 6(x⁵ – 2x³ + x)
= 6x(x⁴ – 2x² +1)
= 6x(x² – 1)²
f'(x) ≤ 0
⇒ 6x(x² – 1)² < 0
f(x) is decreasing when (-∞, -1) ∪ (-1, 0)
f'(x) > 0
f(x) is increasing when (0, 1) ∪ (1, ∞)

iv) x³(x – 2)²
Solution:
f'(x) = x³. 2(x – 2) + (x – 2)².3x²
= x² (x – 2) [2x + 3 (x- 2)]
= x² (x – 2) (2x + 3x – 6)
= x² (x – 2) (5x – 6) ∀ x ∈ R, x² ≥ 0
For increasing, f'(x) = 0
x²(x – 2) (5x – 6) > 0
x ∈ (-∞, \(\frac{6}{5}\)) ∪ (2, ∞)
For decreasing, f'(x) < 0
x²(x – 2) (5x – 6) < 0
x ∈ (\(\frac{6}{5}\), 2)

v) xe^x
Solution:
f'(x) = x . e^x + e^x. 1 = e^x(x + 1)
e^x is positive for all real values of x
f'(x)>0 ⇒ x + 1 > 6 ⇒ x > – 1
f(x) is increasing when x > – 1
f(x) < 0 ⇒ x + 1 < 0 ⇒ x < -1
f(x) is decreasing when x < – 1

vi) \(\sqrt{(25-4x^{2})}\)
Solution:
f(x) is real only when 25 – 4x² > 0
-(4x² – 25) > 0
-(2x + 5) (2x – 5) > 0
∴ x lies between –\(\frac{5}{2}\) and \(\frac{5}{2}\)
Domain of f = (-\(\frac{5}{2}\), \(\frac{5}{2}\))
f'(x) = \(\frac{1}{2 \sqrt{25-4 x^{2}}}\) (-8x)
= –\(\frac{4x}{\sqrt{25-4 x^{2}}}\)
f(x) is increasing when f'(x) > 0
⇒ \(\frac{-4x}{\sqrt{25-4 x^{2}}}\) > 0
i.e., x < o
f(x) is increasing when (-\(\frac{5}{2}\), 0)
f(x) is decreasing when f'(x) < 0
⇒ –\(\frac{4x}{\sqrt{25-4 x^{2}}}\) < 0
∴ x > 0
f(x) is decreasing when (0, \(\frac{5}{2}\)).

vii) ln (ln(x)); x > 1.
Solution:
f'(x) = –\(\frac{1}{lnx}•\frac{1}{x}\)
f(x) is decreasing when f'(x) > 0
\(\frac{1}{x.ln x}\) >0
⇒ x. In x > 0
ln x is real only when x > 0
∴ ln x < 0 = ln 1
i.e., x > 1
f(x) is increasing when x > 1 i.e., in (1, ∞)
f(x) is decreasing when f'(x) < 0 ⇒ ln x > 0 = ln 1
i.e., x < 1
f(x) is decreasing in (0, 1)

viii) x³ + 3x² – 6x + 12.
Solution:
f(x) = x³ + 3x² – 6x + 12
f(x) = 3x² + 6x – 6
= 3(x² + 2x – 2)
= 3((x + 1)² – 3)
= 3[(x + 1) + √3] [(x + 1) – √3]
= 3(x + (1 + √3) (x + (1 – √3 )
f (x) < 0
⇒ x = -(1+ √3 ) or -(1 – √3 )
x = -1 – √3 or √3 – 1
f(x) is decreasing in (-1 -√3 , √3 -1)
f (x) > 0
f(x) increasing when (-∞, -1 – √3 ) ∪ (√3 – 1, ∞)

Question 2.
Show that f(x) = cos²x is strictly increasing on (0, π/2).
Solution:
f(x) = cos² X
⇒ f(x) = 2 cos x (-sin x)
= -2 sin x cos x
= -sin 2x
Since 0 < x < \(\frac{\pi}{2}\)
⇒ 0 < 2x < π
Since ‘sin x’ is +ve between 0 and π
∴ f(x) is clearly -ve.
∴ f'(x) < 0
∴ f(x) is strictly decreasing.

Question 3.
Show that x + \(\frac{1}{x}\) is increasing on [1, ∞)
Solution:
Let f(x) = x + \(\frac{1}{x}\)
f'(x) = 1 – \(\frac{1}{x^{2}}\) = \(\frac{x^{2}-1}{x^{2}}\)
Since x ∈ [1, ∞) = \(\frac{x^{2}-1}{x^{2}}\) > 0
∴ f'(x) > 0
∴ f(x) is increasing.

Question 4.
Show that \(\frac{x}{1+x}\) < ln (1 + x) < x ∀ x > 0
Solution:
Let f(x) = ln(1 + x)- \(\frac{x}{1+x}\)
= ln(1 + x) – \(\frac{1+x-1}{1+x}\)
= ln(1 + x) – 1 + \(\frac{1}{1+x}\)
f'(x) = \(\frac{1}{1+x}\) – \(\frac{1}{(1+x)^{2}}\)
= \(\frac{1+x-1}{(1+x)^{2}}\)
= \(\frac{x}{(1+x)^{2}}\) > 0 since x > 0
f(x) is increasing when x > 0
∴ f(x) > f(0)
f(0) = ln 1 – \(\frac{0}{1+0}\) = 0 – 0 = 0
Since xe [1, ∞) =
ln (1 + x) – \(\frac{x}{1+x}\) > 0
⇒ ln (1 + x) > \(\frac{x}{1+x}\) ……… (1)
Let g(x) = x – ln (1 + x)
g'(x) = 1 – \(\frac{x}{1+x}=\frac{1+x-1}{1+x}\)
= \(\frac{x}{1+x}\) > 0 since x > 0
g(x) is increasing when x > 0
i.e., g(x) > g(0)
g(0) = 0 – ln (1) = 0 – 0 = 0
∴ x – ln (1 + x) > 0
x > ln(1 + x) ………….. (2)
From (1), (2) we get
\(\frac{x}{1+x}\) < ln (1 + x) < x ∀ x > 0

III.

Question 1.
Show that \(\frac{x}{1+x^{2}}\) < tan^-1 x < x when x > 0.
Solution:
Let f(x) = tan^-1 x – \(\frac{x}{1+x^{2}}\)

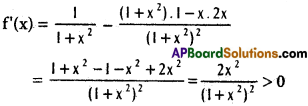
f(x) is increasing when x > 0
f(x) > f(0)
But f(0) = tan^-1 0 – 0 = 0 – 0 = 0
i.e., f(x) > 0

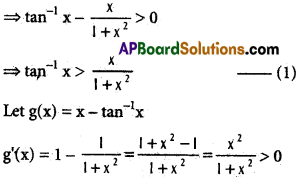
g(x) is increasing when x > 0
g(x) > g(0)
g(0) = 0 – tan^-1 0 = 0 – 0 = 0
∴ x – tan^-1 x > 0
⇒ x > tan^-1 x ………. (2)
From (1), (2) we get
\(\frac{x}{1+x^{2}}\) <tan^-1 x< x for x > 0

Question 2.
Show that tan x > x for all (0, \(\frac{\pi}{2}\))
Solution:
Let f(x) = tan x – x
f'(x) = sec² x – 1 > 0 for every
x ∈ (0, \(\frac{\pi}{2}\))
f(x) is increasing for every x ∈ (0, \(\frac{\pi}{2}\))
i.e., f(x) > f(0)
f(0) = tan 0 – 0 = 0 – 0 = 0
∴ tan x – x > 0
⇒ tan x > x for every x ∈ (0, \(\frac{\pi}{2}\))

Question 3.
If x ∈ (0, \(\frac{\pi}{2}\)) then show that \(\frac{2x}{\pi}\) < sin x < x.
Solution:
Let f(x) = x – sin x
f(x) = 1- cos x > 0 for every x ∈ (0, \(\frac{\pi}{2}\))
f(x) is increasing for every x ∈ (0, \(\frac{\pi}{2}\))
⇒ f(x) > f(0)
f(0) = 0 – sin 0 = 0 – 0 = 0
∴ x – sin x > 0
⇒ x > sin x ………….. (1)
Let g(x) = sin x – \(\frac{2x}{\pi}\)
g'(x) = cos x – \(\frac{2}{\pi}\) > 0 for every x ∈ (0, \(\frac{\pi}{2}\))
g(x) is increasing in (0, \(\frac{\pi}{2}\))
g(x) > g(0)
g(0) = sin 0 – 0 = 0 – 0 = 0
∴ sin x – \(\frac{2x}{\pi}\) > 0
⇒ sin x > \(\frac{2x}{\pi}\) ………… (2)
From (1), (2) we get
\(\frac{2x}{\pi}\) < sin x < x for every x ∈ (0, \(\frac{\pi}{2}\))

Question 4.
If x e (0,1) then show that 2x < ln [latex]\frac{(1+x)}{(x-1)}[/latex] < 2x [1 + \(\frac{x^{2}}{2(1+x^{2})}\)] Solution:
Let f(x) = ln \(\frac{(1+x)}{1-x}\) – 2x
= ln (1 + x) – ln (1 – x) – 2x

f(x) is increasing ih (0, 1)
i.e., x > 0 ⇒ f(x) > f(0)
f(0) = ln 1 – 0 = 0 – 0 = 0


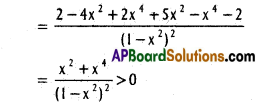
g(x) is increasing when x > 0
g(x) > g(0)
g(0) = 0 – ln 1 = 0 – 0 = 0

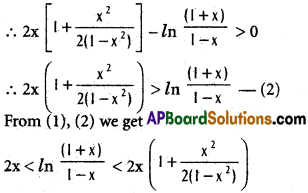
for x ∈ (0,1)

Question 5.
At what point the slopes of the tangents y = \(\frac{x^{3}}{6}-\frac{3x^{3}}{2}+\frac{11x}{2}\) + 12 increases?
Solution:
Equation of the curve is
y = \(\frac{x^{3}}{6}-\frac{3}{2}x^{2}+\frac{11x}{2}\) + 12

Slope = m = \(\frac{x^{2}}{c}-3x+\frac{11}{2}\)
\(\frac{dm}{dx}\) = \(\frac{2x}{2}\) -3 = x – 3
Slope increases ⇒ m > 0
x – 3 > 0
x > 3
The slope increases in (3, ∝)

Question 6.
Show that the functions ln \(\frac{(1+x)}{x}\) and \(\frac{x}{(1+x)ln(1+x)}\) are decrasing on (0, ∞).
Solution:
i)


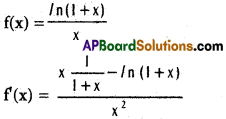
∴ f(x) is decreasing for x ∈ (0, ∝)

ii) let f(x) = \(\frac{x}{(1+x)ln(1+x)}\)

∴ f(x) is decreasing for x ∈ (0, ∝)

Question 7.
Find the intervals in which the function f (x) = x3 – 3×2 + 4 is strictly increasing all x e R.
Solution:
f(x) = x³ – 3x² + 4
f'(x) = 3x² – 6x
f(x) is increasing if f'(x) > 0
3x² – 6x > 0
3x(x – 2) > 0
(x – 0)(x – 2) > 0
f(x) is increasing if x £ (-∞, 0) u (0, ∞)
f(x) is decreasing if f'(x) < 0
(x – 0) (x – 2) < 0
x ∈ (0, 2)

Question 8.
Find the intervals in which the function f(x) = sin⁴x + cos⁴x ∀ x ∈ [0, \(\frac{\pi}{2}\)] is increasing and decreasing.
Solution:
f(x) = sin⁴x + cos⁴x
f(x) = (sin²x)² + (cos²x)²
= (sin²x + cos²x)² – 2sin²x cos²x
= 1 – \(\frac{1}{2}\) sin² 2x
f'(x) = \(\frac{-1}{2}\) 2sin 2x. cos 2x(2)
= -2 sin 2x. cos 2x
= -sin 4x
Let 0 < x < \(\frac{\pi}{4}\)
∴ f(x) is decreasing if f'(x) < 0
⇒ -sinx < 0 ⇒ sinx > 0
∴ x ∈ (0, \(\frac{\pi}{4}\))
f(x) is increasing if f'(x) > 0
⇒ – sinx > 0
⇒ sinx < 0
∴ x ∈ (\(\frac{\pi}{4}\), \(\frac{\pi}{2}\))