Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(a) will help students to clear their doubts quickly.
Intermediate 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(a)
I.
Question 1.
Find the acute angle between the pair of lines represented by the following equations.
(i) x² – 7xy + 12y² = 0
(ii) y² – xy – 6x² = 0
(iii) (x cos α – y sin α)² = (x² + y²) sin² α
(iv) x² + 2xy cot α – y² = 0
Solution:
(i) x² – 7xy + 12y² = 0
a = 1, b = 12, h = –\(\frac{7}{2}\)
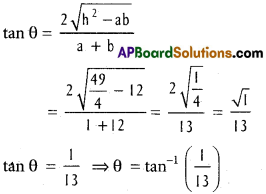
(ii) y² – xy – x² = 0
a = -6, b = 1, h = –\(\frac{1}{2}\)
\(\cos \theta=\frac{|a+b|}{\sqrt{(a-b)^{2}+4 h^{2}}}\)
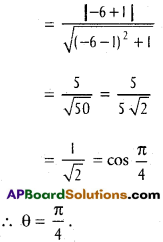
(iii) (x cos α – y sin α)² = (x² + y²) sin² α
x2 cos² α + y² sin² a – 2xy cos α sin α = x² sin² α + y² sin² α
∴ x² (cos² α – sin² α) – 2xy cos α sin α = 0
x².cos 2α – xy sin 2α = 0
a = cos 2α, b = 0, 2h = -sin 2α
\(\cos \theta=\frac{\|\cos 2 \alpha+0\|}{\sqrt{(\cos 2 \alpha-0)^{2}+\sin ^{2} 2 \alpha}}\)
= cos 2α
∴ θ = 2α
(iv) x² + 2xy cot a – y² = 0
a + b = 1 – 1 = 0
∴ θ = \(\frac{\pi}{2}\)
II.
Question 1.
Show that the following pairs of straight lines have the same set of angular bisectors (that is they are equally inclined to each other).
i) 2x² + 6xy + y² = 0,
4x² + 18xy + y² = 0.
ii) a²x² + 2h(a + b) xy + b²y² = 0,
ax² + 2hxy + by² = 0, a + b ≠ 0.
iii) ax² + 2hxy + by² + λ(x² + y²) = 0; (λ ∈ R),
ax² + 2hxy + by² = 0.
Solution:
(i) Combined equation of OA, OB is
2x² + 6xy + y² = 0
Equation of the pair of bisectors is
3(x² – y²) = (2 – 1) xy
3(x² – y2² = xy ………… (1)
Combined equation of OP, OQ is
4x² + 18xy + y² = 0
Equation of the pair of bisectors is
9(x² – y²) = (4 – 1) xy 9(x² – y²) = 3xy
3(x² – y²) = xy ………….. (2)
(1), (2) are same.
∴ OA, OB and OP, OQ are inclined to each other.
(ii) Combined equation of OA, OB is
a²x² + 2h(a + b) xy + b²y² = 0
Equation of the pair of bisectors is
h (a + b) (x² – y²) = (a² – b²) xy
h (a + b) (x² – y²) = (a + b)(a – b) xy
i.e., h(x² – y²) = (a – b) xy ………… (1)
Combined equation of OP, OQ is
ax² + 2hxy + by² = 0
Equation of the pair of bisectors is
h (x² – y²) = (a – b) xy …………. (2)
(1), (2) are same.
∴ OA, OB and OP, OQ are equally inclined to each other.
(iii) Combined equation of OA, OB is
ax² + 2hxy + by² + λ(x² + y²) = 0
(a + λ) x² + 2hxy + (b + λ) y² = 0
Equation of the pair of bisectors of OA, OB is
h (x2 – y2) = (a + λ – b – λ)xy
= (a – b)xy ……….. (1)
Combined equation of OP, OQ is
ax² + 2hxy + by² = 0
Equation of the pair of bisectors of OP, OQ is
h(x² – y²) = (a – b) xy …………. (2)
(1), (2) are same.
∴ OA, OB and OP, OQ are equally inclined to each other.
![]()
Question 2.
Find the value of h, if the slopes of the lines represented by 6x² + 2hxy + y² = 0 are in the ratio 1: 2.
Solution:
Combined equation of the lines is
6x² + 2hxy + y² = 0
Suppose individual equations of the given lines are y = m1x and y = m2x

Question 3.
If ax² + 2hxy + by² = 0 represents two straight lines such that the slope of one line is twice the slope of the other, prove that 8h² = 9ab.
Solution:
Combined equation of the lines is
ax² + 2hxy + by² =0
Suppose, y = m1x and y = m2x are the individual equations of the lines.
∴ m1 + m2 = –\(\frac{2h}{b}\), m1m2 = \(\frac{a}{b}\)
Given m2 = 2m1
∴ 3m1 = –\(\frac{2h}{b}\) ; 2m1² = \(\frac{a}{b}\)
m1 = –\(\frac{2h}{3}\) ; m1² = \(\frac{a}{2b}\)
∴ (-\(\frac{2h}{3b}\))² = \(\frac{a}{2b}\)
\(\frac{4 h^{2}}{9 b^{2}}=\frac{a}{2 b}\)
8h² = 9ab.
Question 4.
Show that the equation of the pair of straight lines passing through the origin and making an angle of 30° with the line 3x – y – 1 = 0 is 13x² + 12xy – 3y² = 0
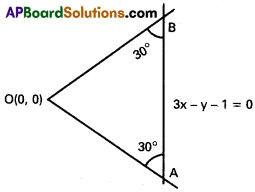
Solution:
Equation of AB is 3x – y – 1 = 0
OA, OB make an angle of 30° with AB and pass through the origin.
Suppose slope of OA is m
∴ Equation of OA is
y – 0 = m (x – 0) = mx or mx – y = 0
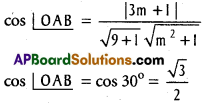
∴ \(\frac{\sqrt{3}}{2}=\frac{|3 m+1|}{\sqrt{10} \sqrt{m^{2}+1}}\)
Squaring and cross multiplying
\(\frac{3\left(m^{2}+1\right)}{4}=\frac{(3 m+1)^{2}}{10}\)
15(m² + 1) = 2 (3m + 1)²
15m² + 15 = 2 (9m² + 6m + 1)
= 18m² + 12m + 2
3m² + 12m -13 = 0
Suppose m1, m2 are two roots of the equation
m1 + m2 = -4, m1 m2 = \(\frac{-13}{3}\)
Combined equation of OA and OB is
(m1x – y) (m2x – y) = 0
m1m2x² – (m1 + m2) xy + y² = 0
\(\frac{-13}{3}\)x² + 4xy + y² = 0
-13 x² + 12xy + 3y² = 0 or
13x² – 12xy – 3y² = 0
Question 5.
Find the equation to the pair of straight lines passing through the origin and making an acute angle a with the straight line x + y + 5 = 0.
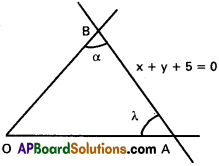
Solution:
Equation of AB is x + y + 5 = 0 ……….. (1)
Slope of AB = – λ
Suppose OA and OB are the required lines
Suppose equation of OA is
y = mx ⇒ mx – y = 0
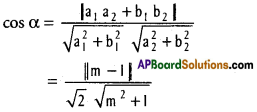
2(m² + 1) cos² α = (m – 1)²
2(m² + 1) = \(\frac{(m-1)^{2}}{\cos ^{2} \alpha}\) = (m – 1)² sec² α.
2m² + 2 = m² sec² α – 2m sec² α + sec² α.
m² (sec² α – 2) – 2m sec² α + (sec² α – 2) = 0
m1 + m2 = \(\frac{2 \sec ^{2} \alpha}{\sec ^{2} \alpha-2}\), m1m2 = 1
Combined equation of OA and OB is
(y – m1x) (y – m2x) = 0
y² (m1 + m2) xy + m1m2 x² = 0

Combined equation of OA and OB is
x² + 2xy sec 2a + y² = 0
Question 6.
Show that the straight lines represented by (x + 2a)² – 3y² = 0 and x = a form an equilateral triangle.
Solution:
Combined equation of OA, OB is
(x + 2a)² – 3y² = 0
(x + 2a)² – (√3y)² =0
(x + 2a + √3 y) (x + 2a – √3 y) = 0
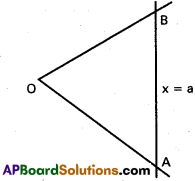
Equation of OA is
x + √3y + 2a = 0 ………….. (1)
Equation of OB is
x – √3y + 2a = 0 ………. (2)
Equation of AB is x – a = 0
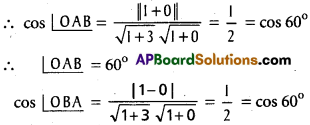
∴ ∠OBA =60°
∴ ∠AOB = 180°- (∠OAB + ∠OBA)
= 180° – (60° + 60°)
= 180° – 120°
= 60°
∴ ∆OAB is an equilateral triangle.
![]()
Question 7.
Show that the pair of bisectors of the angles between the straight lines (ax + by)² = c (bx – ay)², c > 0 are parallel and perpen-dicular to the line ax+ by + k= 0.
Solution:
Combined equation of the given lines is (ax + by)² = c (bx – ay)²
a²x² + b²y² + 2ab xy = c (b²x² + a²y² – 2abxy)
= cb²x² +ca²y² – 2cabxy
(a² – cb²)x² + 2ab (1 + c²) xy + (b² – ca²)y² = 0
Equation of the pair of bisectors is
h (x – y²) = (a – h) xy ^
ab (1 + c) (x² – y²)
= (a² – cb² – b² + ca²) (x² – y²) = 0
= (a² – b²)(1 + c) xy.
i.e., ab (x² – y²) – (a² – b²) xy = 0
(ax + by) (bx – ay) = abx² – a2xy +b²xy – aby²
= ab(x² – y²) – (a² – b²)xy
∴ The equation of the pair of bisectors are (ax + by) (bx – ay) = 0
The bisectors are ax + by = 0 and bx – ay = 0
ax + by = 0 is parallel to ax + by + k = 0
bx – ay = 0 is perpendicular to ax + by +k=0.
Question 8.
The adjacent sides of a parallelogram are 2x² – 5xy + 3y² = 0 and one diagonal is x + y + 2 = 0. Find the vertices and the other diagonal.
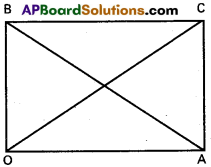
Solution:
Combined equation of OA and OB is 2x² – 5xy + 3y² = 0
Equation of AB is x + y+ 2 = 0
y = -(x + 2)
Substituting in (1)
2x² + 5x (x + 2) + 3(x +2)² = 0
2x² + 5x² + 10x + 3(x² + 4x + 4) = 0
7x² + 10x + 3x² + 12x + 12 = 0
10x² + 22x + 12 = 0
5x² + 11x + 6 = 0
(x + 1) (5x + 6) = 0
x + 1 = 0 or 5x + 6 = 0
x = -1 or 5x = -6
x = –\(\frac{6}{5}\)
y = -(x + 2)
x = -1 ⇒ y = – (-1 + 2) = – 1
⇒ co-ordinates of A are (-1, -1)
x = –\(\frac{6}{5}\) ⇒ y = -(\(\frac{6}{5}\)+ 2) = –\(\frac{4}{5}\)
⇒ co-ordinates of B are (-\(\frac{6}{5}\), –\(\frac{4}{5}\))
Suppose the diagonals AB, OC intersect in O’ O’ bisects AB and OC.
Suppose co-ordinates of C are (x, y)
Midpoint of OC = Midpoint of AB

∴ The vertices are O(0, 0), A(-1, -1)
C(-\(\frac{11}{5}\), –\(\frac{9}{5}\)), B(-\(\frac{6}{5}\), –\(\frac{4}{5}\))
Question 9.
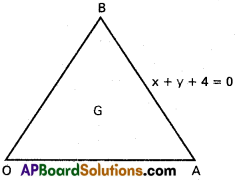
Find the centroid and the area of the triangle formed by the following lines.
(i) 2y² – xy – 6x² = 0, x + y + 4 = 0
(ii) 3x² – 4xy + y² = 0, 2x – y = 6
Solution:
(i) Combined equation of OA, OB is
2y² – xy – 6x² = 0 ………… (1)
Equation of AB is x + y + 4 = 0
y = – (x + 4) ………… (2)
Substituting in (1)
2(x + 4)² + x (x + 4) – 6x² = 0
2(x² + 8x + 16) + x² + 4x – 6x² = 0
2x² + 16x + 32 + x² + 4x – 6×2 = 0
-3x² + 20x + 32 = 0
3x² – 20x – 32 = 0
(3x + 4) (x-8) = 0
3x + 4 = 0 or x – 8 = 0
x = –\(\frac{4}{3}\) or 8
Case (i) : x = –\(\frac{4}{3}\)
y = – (x + 4)
= -(\(\frac{-4}{3}\) + 4) = –\(\frac{8}{3}\)
Co – ordinates of A are (-\(\frac{4}{3}\), –\(\frac{8}{3}\))
Case (ii) : x = 8
y = -(x + 4) = – (8 + 4) = – 12
Co-ordinates of B are (8, – 12)
Suppose G is the centroid of ∆ AOB
Co-ordinates of G are

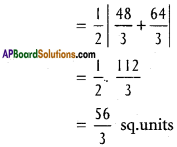
(ii) Combined equation of OA, OB is
3x² – 4xy + y² = 0 ……………. (1)
Equation of AB is 2x – y = 6
y = 2x – 6 ……………. (2)
Substituting in (1)
3x² – 4x (2x – 6) + (2x – 6)² = 0
3x² + 8x² + 24x + 4x² + 36 – 24x = 0
– x + 36 = 0
x² – 36 = 0
(x + 6) (x – 6) = 0
x + 6 = 0 or x – 6 = 0
x = – 6 or 6
y = 2x – 6
x = 6 ⇒ y = 12 – 6 = 6
Go -ordinates of A are (6, 6)
x = -6 ⇒ y = – 12 – 6 = -18
Co-ordinates of B are (-6, -18)
Co-ordinates of G ate
(\(\frac{0+6-6}{3}\), \(\frac{0+6-18}{3}\)) = (0, -4)
∆OAB = \(\frac{1}{2}\)|x1y2 – x2y1|
= \(\frac{1}{2}\)|16 (-18) – (-6). 6|
= \(\frac{1}{2}\)|- 108 + 36|
= \(\frac{1}{2}\) . 72 =36 sq.units
Question 10.
Find the equation of the pair of lines intersecting at (2, -1) and
(i) perpendicular to the pair
6x² – 13xy – 5y² = 0 and
(ii) parallel to the pair
6x² – 13xy – 5y² = 0.
Solution:
Equation of OA, OB is 6x² – 13xy – 5y² = 0
(i) Equation of the pair of lines through (x1 y1) and perpendicular to
ax² + 2hxy + by² = 0 is
b(x – x1)² – 2h(x – x1) (y – y1) + a (y – y1)² = 0
Equation of the perpendicular pair of lines is
-5(x – 2)² + 13(x – 2) (y + 1) + 6(y+ 1)² =0
-5(x² – 4x + 4) + 13(xy + x – 2y – 2) + 6(y² + 2y + 1) = 0
-5x² + 20x – 20 + 13xy + 13x – 26y – 26 + 6y² + 12y + 6 = 0
-5x² + 13xy + 6y² + 33x – 14y – 40 = 0
or 5x² – 13xy – 6y² – 33x + 14y + 40 = 0
(ii) Equation of the pair of lines through (x1, y1) and parallel to ax² + 2hxy + by² = 0 is
a(x – x1)² + 2h (x – x1) (y – y1) + b (y – y1)² = 0
Equation of the pair of parallel lines is
6(x- 2)² – 13(x – 2) (y + 1) – 5(y + 1)² = 0
6(x² – 4x + 4) – 13(xy + x – 2y – 2) – 5(y² + 2y + 1) = 0
6x² – 24x + 24 – 13xy – 13x + 26y + 26 – 5y² – 10y – 5 = 0
6x² – 13xy – 5y² – 37x + 16y + 45 = 0.
![]()
Question 11.
Find the equation of the bisector of the acute angle between the lines
3x – 4y + 7 = 0 and 12x + 5y – 2 = 0
Solution:
Given lines
3x – 4y + 7 = 0 ………….. (1)
12x + 5y – 2 = 0 ………… (2)
The equations of bisector’s angles between (1) & (2) is
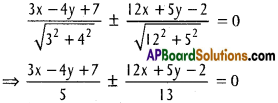
13 (3x – 4y + 7) ± 5 (12x + 5y- 2) = 0
(39x – 52y + 51) ± (60x + 25y – 10) = 0
(i) 39x- 52y + 51 + 60x + 25y- 10 = 0
99x-27y + 41 = 0 ……… (3)
(ii) (39x – 52y + 51) – (60x + 25y- 10) = 0
39x – 52y + 51 – 60x – 25y +10 = 0
– 21x – 77y + 61 =0
21x + 77y- 61 = 0 ……… (4)
Let ‘θ’ be the angle between (1), (4)
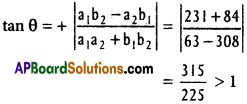
∴ (4) is obtuse angle bisector, then other one (3) is the accute angle bisector.
∴ 99x – 27y + 41 = 0 is the accute angle bisector.
Question 12.
Find the equation of the bisector of the obtuse angle between the lines x + y – 5 = 0 and x – 7y + 7 = 0
Solution:
Given lines
x + y- 5 = 0 ………. (1)
x – 7y + 7 = 0 ……..(2)
The equations of bisectors of angles between (1), (2) is
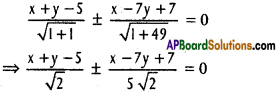
⇒ (5x + 5y-25)±(x-7y + 7) = 0
(i) 5x + 5y – 25 + x – 7y + 7 = 0
6x – 2y – 18 = 0
3x-y-9 = 0 ………. (3)
(ii) (5x + 5y – 25) – (x – 7y + 7) = 0
4x+ 12y – 32 = 0
x + 3y – 8 = 0 ……… (4)
Let ‘θ’ be the angle between (1), (4)
![]()
∴ (4) is the ocute angle bisector, then other one 3x – y – 9 = 0 is the obtuse angle bisector.
III.
Question 1.
Show that the lines represented by (lx + my)² – 3(mx – ly)² = 0 and lx + my + n = 0 form an equilateral triangle with area \(\frac{n^{2}}{\sqrt{3}\left(l^{2}+m^{2}\right)}\).
Solution:
Combined equation of A and is
(lx + my)² – 3(mx – ly)² = 0
l²x² + m²y² + 2lmxy – 3m²x² – 3l²y² + 6 lmxy = 0
(l² – 3m²) x² + 8lmxy + (m² – 3l²) y² = 0
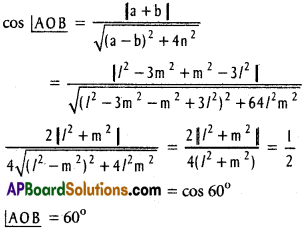
Combined equation of the bisectors of OA
and OB is h (x² – y²) = (a – b) xy
4 lm (x² – y²) = (l² – 3m² – m² + 3l²) xy
4 lm (x² – y²) = 4(l² – m²) xy
lmx² – (l² – m²)xy – lmy² = 0
(lx – my) (mx – ly) = 0
lx + my = 0 and mx – ly = 0
∴ The bisectors mx – ly = 0 is perpendicular to AB whose equation lx + my + n = 0
OAB is an scales triangle and ∠AOB = 60°
OAB is an equalated tringle
P = Length of the X lan prove P and AB
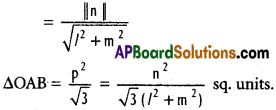
Question 2.
Show that the straight tines represented by 3x² + 48xy + 23y² = 0 and 3x – 2y + 13 = 0 form an equilateral triangle of area \(\frac{13}{\sqrt{3}}\) sq.umts.
Solution:
Combined equation of OA, OB is
3x² + 48xy + 23y² = 0 …………. (1)
Equation of AB is 3x – 2y + 13 = 0 …….. (2)
(1) can be written as
(9x² – 12xy + 4y²) – 3(4x² + 12xy + 9y²) = 0
i.e., (3x – 2y)² – 3(2x + 3y)² = 0
⇒ [(3x – 2y) + √3(2x +3y)] [(3x – 2y) – √3(2x+3y)] = 0
⇒ [(3 + 2√3)x+ (3√3 – 2)y] [(3 – 2√3)x – (3√3 + 2)y]=0
Equation of OA is
(3 + 2√3)x – (3√3 – 2)y = 0 ………….. (1)
Equation of OB is
(3 – 2√3)x – (3√3 +2)y =0 ………… (2)

∴ OAB is an equilateral triangle.

Question 3.
Show that the equation of the pair of lines bisecting the angles between the pair of bisectors of the angles between the pair of lines ax² + 2hxy + by² = 0 is (a – b) (x² – y²) + 4hxy = 0
Solution:
Equation of the given lines is
ax² + 2hxy + by² = 0
Equation of the pair of bisectors is
h(x² – y²) = (a – b)xy …………. (1)
hx² – hy² – (a – b) xy = 0
∴ A = h, B = -h, 2H = -(a – b)
Equation of the pair of bisectors of (1) is
H(x² – y²) = (A – B) xy
–\(\frac{(a-b)}{2}\)(x² – y²) = 2hxy
-(a – b) (x² – y²) = 4hxy
or (a – b) (x² – y²) + 4hxy = 0
∴ Equation of the pair of bisectors of the pair of bisectors of ax² + 2hyx + by² = 0 is
(a – b) (x² – y²) + 4hxy = 0.
![]()
Question 4.
If one line of the pair of lines ax² + 2hxy + by² = 0 bisects the angle between the co-ordinate axes, prove that (a + b)²= 4h².
Solution:
The angular bisectors of the co-ordinate axes are:
y = ±x
Case (i) :
y = x is one of the lines of
ax² + 2hxy + by² = 0
x²(a + 2h + b) = 0
a + 2h + b = 0 ………….. (1)
Case (ii) :
y = – x is one of the lines of
ax² + 2hxy + by² = 0
x² (a – 2h + b) = 0
a – 2h + b = 0 ………. (2)
Multiplying (1) and (2), we get
(a + b + 2h).(a + b – 2h) = 0
(a + b)² – 4h² = 0
(a + b)² = 4h².
Question 5.
If (α, β) is the centroid of the triangle formed by the lines ax² + 2hxy + by² =0 and lx + my = 1, prove that
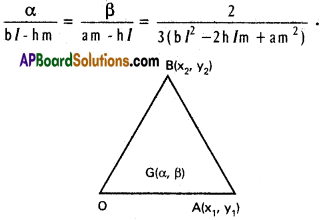
Solution:
Combined equation of OA, OB is
ax² + 2hxy + by² = 0 …………. (1)
Equation of AB is lx + my = 1
my = 1 – lx
\(y=\frac{1-1 x}{m}\) …………. (2)
Substituting in (1)
ax² + 2hx\(\frac{(1-b)}{m}\) + b\(\frac{(1-1 x)^{2}}{m^{2}}\) = 0
am²x² + 2hmx(1 – lx) + b(1 + l²x² – 2lx) = 0
am²x² + 2hmx – 2hlmx² + b + bl²x² – 2blx = 0
(am² – 2hlm + bl²)x² – 2(bl – hm)x + b = 0
Suppose coordinates of A are (x1, y1) and B are (x2, y2)
x1 + x2 = \(\frac{2(b /-h m)}{a m^{2}-2 h / m+b l^{2}}\) …………. (3)
A and B are points on
lx + my = 1
lx1 + my1 = 1
lx2 + my2 = 1
l(x1 + x2) + m(y1 + y2) = 2
m(y1 + y2) = 2 – l(x1 + x2)

Co-ordinates of the vertices are
O(0, 0), A(x1, y1), B(x2, y2)
Co-ordinates of G are


Question 6.
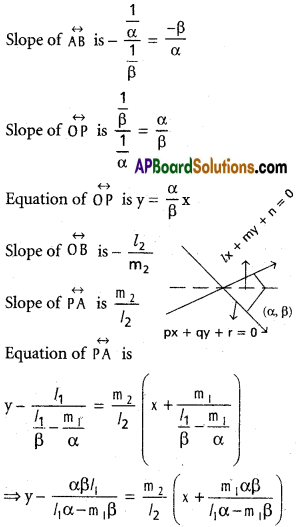
Prove that the distance from the origin to the orthocentre of the triangle formed by the lines \(\frac{x}{\alpha}+\frac{y}{\beta}\) = 1 and ax² + 2hxy + by² = 0 is (α² + β²)1/2 \(\left|\frac{(a+b) \alpha \beta}{a \alpha^{2}-2 h \alpha \beta+b \beta^{2}}\right|\).
Solution:
Let ax² + 2hxy + by² = 0 represent the lines
l1x + m1y = 0 ………… (1)
l2x + m2y = 0 ………… (2)
∴ (l1x + m1y) (l2x + m2y) = ax² + 2hxy + by²
Comparing both sides
l1l2 = a, m1m2 = b, l1m2 + l2 m1 = 2h
Given line is lx + my =1 ……….. (3)
Clearly the origin O is the point of intersection of (1) & (2)
Let A be the point of intersection of (1) & (3)
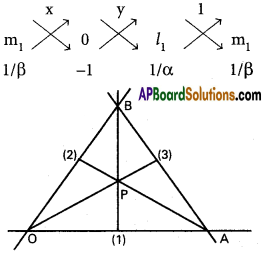
By the method of cross multiplication,
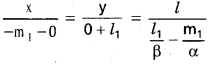
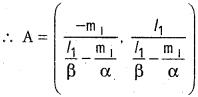
Let B be the point of intersection of (2) & (3)
Let P be the orthocentre of ∆ OAB.
⇒ yl2(l1α – m1β) – αβl1l2 = m2(x(l1α – m1β) + m1αβ)
⇒ (l1α – m1P) (m2x – l2y) = m1m2αβ + l1l2αβ


![]()
Question 7.
The straight line lx + my + n = 0 bisects an angle between the pair of lines of which one is px + qy + r = 0. Show that the other line is (px + qy + r) (l² + m²) – 2(lp + mq) (lx + my + n) = 0.
Solution:
lx + my + n – 0 is a bisector and let (a, P) be any point on it so that
lα + mβ + n = 0 …………….. (1)
The other line will pass through the intersection of given lines and given bisector and hence by p +λq = 0
Its equation is
(px + qy + r) + λ(lx + my + n) = 0 …………….. (2)
Also px + qy + r = 0
If (α, β) be a point on the bisector then its perpendicular distance from the lines (2) and (3) is same.
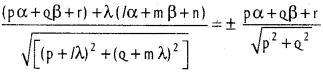
Putting lα + mβ + n = 0 by (1) in the above and cancelling pα + qβ + r and then squaring both sides, we get
(p + lλ)² + (q + mλ)² = p² + q² or
2λ(pl + qm)+ λ²(l² + m²) = 0
∴ λ = -2\(\frac{p l+Q m}{l^{2}+m^{2}}\)
Substitute X value in (2),
(px + qy + r) + \(\left(\frac{-2(p /+Q m)}{l^{2}+m^{2}}\right)\) lx + my + n = 0
⇒ (px + qy + r)(l² + m²) -2(pl + qm) (lx + my + n ) = 0