Inter 1st Year Maths 1B Pair of Straight Lines Solutions Ex 4(c)

Practicing the Intermediate 1st Year Maths 1B Textbook Solutions Inter 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c) will help students to clear their doubts quickly.

Intermediate 1st Year Maths 1B Pair of Straight Lines Solutions Exercise 4(c)

I.

Question 1.
Find the equation of the lines joining the origin to the points of intersection of x² + y² = 1 and x + y = 1.
Solution:
The given curves are
x² + y² = 1 …….. (1)
x + y = 1 ……….. (2)
Homogenising (1) with the help of (2) Combined equation of OA and OB is

x² + y² = (x + y)²
= x² + y² + 2xy
i.e., 2xy = 0 ⇒ xy – 0

Question 2.
Find the angle between the lines joining the origin to the points of intersection of y2 = x and x + y = 1.
Solution:
Equation of the centre is y² = x …………. (1)
Equation of AB is x + y = 1 ………. (2)
Hamogonsing (1) with the help of O
Combined equation of A & OB is
y² = x(x + y) = x² + xy
x² + xy – y2 = 0
a + b = 1 – 1 = 0
OA, OB an perpendicular
∴ ∠AOB =90°

II.

Question 1.
Show that the lines joining the origin to the points of intersection of the curve x² – xy + y² + 3x + 3y – 2 = 0 and the straight line x – y – √2 = 0 are mutually perpendicular.
Solution:

Equation of the curve is
x² – xy + y² + 3x + 3y – 2 = 0 ……….. (1)
Equation of AB is x – y – √2 = 0
x – y = √2
\(\frac{x-y}{\sqrt{2}}\) = 1 ………. (2)
Homogenising, (1) with the help of (2) combined equation of OA, OB is
x² – xy + y² + 3x.1 + 3y.1 – 2.1² = 0
x² – xy + y² + 3(x + y)\(\frac{x-y}{\sqrt{2}}\) – 2\(\frac{(x-y)^{2}}{2}\) = 0
x² – xy + y² + \(\frac{3}{\sqrt{2}}\)(x² – y²) – (x² – 2xy + y²) = 0
x² – xy + y² + \(\frac{3}{\sqrt{2}}\)x² – \(\frac{3}{\sqrt{2}}\)y² – x² + 2xy – y² = 0
\(\frac{3}{\sqrt{2}}\)x² + xy – \(\frac{3}{\sqrt{2}}\)y² = 0
a + b = \(\frac{3}{\sqrt{2}}\) – \(\frac{3}{\sqrt{2}}\) = 0
∴ OA, OB are perpendicular.

Question 2.
Find the values of k, if the lines joining the origin to the points of intersection of the curve 2x² – 2xy + 3y² + 2x – y – 1 = 0 and the line x + 2y = k are muiually perpendicular.
Solution:
Given equation of the curve is
S ≡ 2x² – 2xy + 3y² + 2x – y – 1 = 0 ……….. (1)
Equation of AB is x + 2y = k

\(\frac{x+2y}{k}\) = 1
Homogenising, (1) with the help of (2), combined equation of OA, OB is
2x² – 2xy + 3y² + 2x.1 – y.1 – 1² = 0
2x² – 2xy + 3y² + 2x\(\frac{x+2y}{k}\) – y\(\frac{x+2y}{k}\) – \(\frac{(x+2y)^{2}}{k^{2}}\) = 0
Multiplying with k²
2k²x² – 2k²xy + 3k²y² + 2kx(x + 2y) – ky(x + 2y) – (x + 2y)² = 0
2k²x² – 2k²xy + 3k²y² + 2kx² + 4kxy – kxy – 2ky² – x² – 4xy – 4y² = 0
(2k² + 2k – 1)x² + (-2k² + 3k – 4) xy + (3k² – 2k – 4) y² = 0
Since OA, OB are perpendicular.
Co-efficient x² + Co-efficient of y² = 0
2k² + 2k – 1 + 3k² – 2k – 4 = 0
5k² = 5 ⇒ k² = 1
∴ k = ± 1

Question 3.
Find the angle between the lines joining the origin to the points of intersection of the curve x² + 2xy + y² + 2x + 2y – 5 = 0 and the line 3x – y + 1 = 0
Solution:

Equation of the curve is
x² + 2xy + y² + 2x + 2y- 5 = 0 …….. (1)
Equation of AB is 3x – y + 1 = 0
y – 3x = 1…………. (2)
Homogenising (1) with the help of (2), combined equation of OA, OB is
x² + 2xy + y² + 2x.1 + 2y.1 – 5.1² = 0
x² + 2xy + y² + 2x(y – 3x) + 2y(y – 3x) – 5 (y – 3x)² = 0
x² + 2xy + y² + 2xy – 6x² + 2y² – 6xy – 5(y² + 9x² – 6xy) = 0
– 5x² – 2xy + 3y² – 5y² – 45x² + 30 xy = 0
-50x² + 28xy – 2y² = 0
i.e, 25x² – 14xy + y² = 0
Suppose θ is the angle between OA and OB

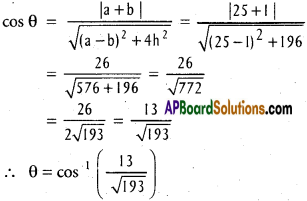
III.

Question 1.
Find the condition for the chord lx + my = 1 of the circle x² + y² = a² (whose centre is the origin) to subtend a right angle at the origin.
Solution:

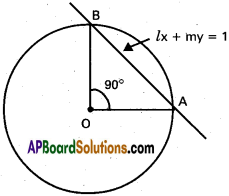
Equation of the circle is x² + y² = a² ………. (1)
Equation of AB is lx + my = 1 ……….. (2)
Homogenising (1) with the help of (2)
Gombined equation of OA, OB is
x² + y² = a².l²
x² + y² = a² (lx + my)²
= a²(l²x² + m²y² + 2lmxy)
= a²l²x² + a²m²y² + 2a²lmxy
i.e., a²l²x² + 2a²lmxy + a²m²y² – x² – y² = 0
(a²l² – 1) x² + 2a² lmxy + (a²m² – 1)y² = 0
Since OA, OB are perpendicular
Co-efficient of x² + co-efficient of y² = 0
a²l² – 1 + a²m² – 1 = 0
a²(l² + m²) = 2
This is the required condition.

Question 2.
Find the condition for the lines joining the origin to the points of intersection of the circle x² + y² = a² and the line lx + my = 1 to coincide.
Solution:

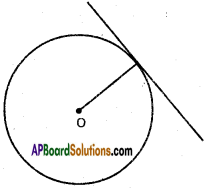
Equation of the circle is
x² + y² = a² ………. (1)
Equation of AB is lx + my = 1 ……….. (2)
Homogenising (1) with the help of (2)
Combined equation of OA, OB is
x² + y² = a².l²
= a²(lx + my)²
= a²(l²x² + m²y² + 2lmxy)
i.e., x² + y² = a²l²x² + a²m²y² + 2a²lmxy
(a²l² – 1)x² + 2a²lmxy + (a²m² – 1)y² = 0
Since OA, OB are coincide
⇒ h² = ab
a⁴ l²m² = (a²l² – 1)(a²m² – 1)
a⁴ l²m² = a⁴ l²m² – a²l² – a² m² + 1
∴ a²l² – a²m² +1=0
a² (l² + m²) = 1
This is the required condition.

Question 3.
Write down the equation of the pair of straight lines joining the origin to the points of intersection of the line 6x – y + 8 = 0 with the pair of straight lines 3x² + 4xy – 4y² – 11x + 2y + 6 = 0. Show that the lines so obtained make equal angles with the coordinate axes.
Solution:
Given pair of lines is
3x² + 4xy – 4y² – 11x + 2y + 6 = 0 ……….. (1)
Given line is
6x – y + 8 = 0 ⇒ \(\frac{6x-y}{-8}\) = 1
⇒ \(\frac{y-6x}{8}\) = 1
Homogenising (1) w. r. t. (2)
3x² + 4xy – 4y² – (11x – 2y) (\(\frac{y-6x}{8}\)) = 6(\(\frac{y-6x}{8}\))² = 0
64[3x² + 4xy – 4y²] – 8[11xy – 66x² – 2y² + 12xy] + 6[y² + 36x² – 12xy] = 0
936x² + 256 xy – 256 xy – 234y² = 0
∴ 468x² – 117y² = 0 …….. (3)
⇒ 4x² – y² = 0
is eq. of pair of lines joining the origin to the point of intersection in.
The eq. pair of angle bisectors to (3) is
h(x² – y²) – (a – b)xy = 0
0(x² – y²) – f4 – l)xy = 0
⇒ xy = 0
x = 0 or y = 0 [Eqs. is of coordinate axes]
∴ The pair of lines are equally inclined to the co-ordinate axes.