Use these Inter 1st Year Maths 1B Formulas PDF Chapter 3 The Straight Line to solve questions creatively.
Intermediate 1st Year Maths 1B The Straight Line Formulas
→ Equation of a horizontal line is y = k
→ Equation of a vertical line is x = h
→ If ‘θ ‘ is the inclination of a line then slope = m = tan θ
→ If m1 m2 are slopes of two lines and ‘θ ‘ is angle between them then tan θ = \(\frac{m_{1}-m_{2}}{1+m_{1} m_{2}}\)
→ If two lines are parallel then their slopes are equal i.e., m1 = m2
→ If two lines are perpendicular, then m1m2 = -1
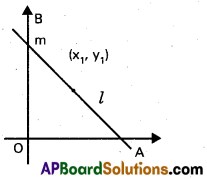
→ Equation of a line passing through (x1, y1) with slope ‘m’ is y – y1 = m(x – x1)
→ Equation of a line passing through origin with slope m is y = mx
→ Equation of the line passing through (x1, y1) and (x2, y2) is \(\) (or) (x – x1)(y1 – y2) = (y – y1)(x1 – x2)
→ Equation of the line with slope’m’ and having
- y-intercept ‘c’ is y = mx + c (slope intercept form)
- x-intercept ‘a’ is y = m(x – a)
![]()
→ Equation of a line in intercept form is \(\frac{x}{a}+\frac{y}{b}\) = 1
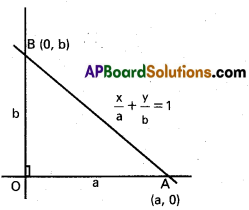
- Intersecting point on X – axis = (a, 0)
- Intersecting point on Y – axis = (0, b)
→ Area of Δle formed by the line with co-ordinate axis is = \(\frac{1}{2}\)|ab|
→ Area of Δle formed by the line ax + by + c = 0 with co-ordinate axis is \(\frac{c^{2}}{2|a b|}\)
→ If a point (x1, y1) divides the line segment between the co-ordinate axes in the ratio l: m then equation of the line is \(\frac{m x}{x_{1}}+\frac{l y}{y_{1}}\) = l + m
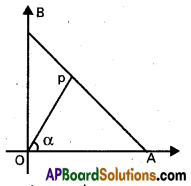
→ Equation of a line in normal form or perpendicular form is x cos α + y sin α = p where ‘α’ is the angle made by the perpendicular with +ve X – axis. ‘p’ is length of normal form origin to the line.
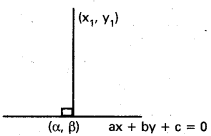
→ Perpendicular distance from (x1, y1) to the line ax + by + c = 0 is \(\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
→ Perpendicular distance from origin to the line ax + by + c = 0 is \(\frac{|c|}{\sqrt{a^{2}+b^{2}}}\)
→ The ratio in which the line L ax + by + c = 0 (ab ≠ 0) divides the line segment AB joining the points A(x1, y1) and B(x2, y2) is –\(\left(\frac{a x_{1}+b y_{1}+c}{a x_{2}+b y_{2}+c}\right)\) or –\(\frac{L_{11}}{L_{22}}\)
where L11 = a1x + b1y + c; L22 = a2x + b2y + c
→ If L11, L22 are having same sign or opposite sign’s then those points lies same side or opposite sides of the line L = 0 respectively.
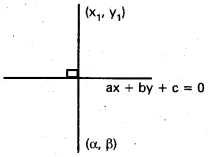
→ If the foot of the perpendicular from (x1, y1) to the line ax + by + c = 0 is (α, β) then \(\frac{\alpha-x_{1}}{a}=\frac{\beta-y_{1}}{b}=\frac{-\left(a x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\)
→ If the image of(x1, y1) w.r.t. the line ax +by + c = 0 is (α, β) then
\(\frac{\alpha-x_{1}}{a}=\frac{\beta-y_{1}}{b}=\frac{-2\left(a x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\)
→ The point of intersection of two lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 is
\(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}} \cdot \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)
![]()
→ If θ |0 ≤ θ ≤ π| is angle between the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 then cos θ = \(\frac{a_{1} a_{2}+b_{1} b_{2}}{\sqrt{a_{1}^{2}+b_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
sin θ = \(\frac{a_{1} b_{2}-a_{2} b_{1}}{\sqrt{a_{1}^{2}+b_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
and tan θ = \(\frac{a_{1} b_{2}-a_{2} b_{1}}{a_{1} a_{2}+b_{1} b_{2}}\)
- The lines are perpendicular ⇔ a1a2 + b1b2 = 0
- Then lines are parallel ⇔ \(\frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\)
→ The equation of a line passing through the point (x1, y1) and parallel to the line ax + by + c = 0 is a(x – x1) + b(y – y1) = 0
→ The equation of a line passing through the point (x1, y1) and perpendicular to ax + by + c = 0 is b(x – x1) – a(y – y1) = 0
→ The distance between the two parallel straight lines a1x + b1y + c1 = 0 and a1x + b1y + c2 = 0 is \(\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}}}\)
→ Area of the parallelogram formed by the lines a1x + b1y + c1 = 0,a 2x + b2y + d1= 0, a2x + b2y + c2 = 0 and a2x + b2y + d2 = 0 is \(\left|\frac{\left(d_{1}-c_{1}\right)\left(d_{2}-c_{2}\right)}{a_{1} b_{2}-a_{2} b_{1}}\right|\)
→ Equation of the line parallel to X – axis and passing through (x1, y1) is y = y1
→ Equation of the line parallel to Y- axis and passing through (x1, y1) is x = x1
Concurrent lines-properties related to a Triangle
Theorem:
The medians of a triangle are concurrent.
Proof:
Let A(x1, y1), B(x2, y2), C(x3, y3) be the vertices of the triangle
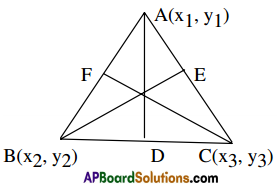
Let D,E,F be the mid points of BC, CA, AB respectively
∴ D = \(\left(\frac{x_{2}+x_{3}}{2}, \frac{y_{2}+y_{3}}{2}\right)\)
E = \(\left(\frac{x_{3}+x_{1}}{2}, \frac{y_{3}+y_{1}}{2}\right)\)
F = \(\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)\)
Slope of \(\overline{A D}\) is \(\frac{\frac{y_{2}+y_{3}}{2}-y_{1}}{\frac{x_{2}+x_{3}}{2}-x_{1}}=\frac{y_{2}+y_{3}-2 y_{1}}{x_{2}+x_{3}-2 x_{1}}\)
Equation of \(\overline{A D}\) is
y – y1 = \(\frac{y_{2}+y_{3}-2 y_{1}}{x_{2}+x_{3}-2 x_{1}}\)(x – x1)
⇒ (y – y1)(x2 + x3 – 2x1) = (x – x1)(y2 + y3 – 2y1)
⇒ L1 = (x – x1)(y2 + y3 – 2y1) – (y – y1)(x2 + x3 – 2x1) = 0
Similarly, the equations to \(\overline{B E}\) and \(\overline{C F}\) respectively are L2 s (x – x2)(y3 + y1 – 2y2) – (y – y2) (x3 + x1 – 2x2) = 0.
L3 = (x – x3)(y1 + y2 – 2y3) – (y – y3) (x1 + x2 – 2x3) = 0.
Now 1. L1 + 1.L2 + 1. L3 = 0
The medians L1 = 0, L2 = 0, L3 = 0 are concurrent.
Theorem:
The altitudes of a triangle are concurrent.
Proof:
Let A(x1, y1), B(x2, y2), C(x3, y3) be the vertices of the triangle ABC. Let AD, BE,CF be the altitudes.
Slope of \(\overline{B C}\) is \(\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\) and AD ⊥ BC
Slope of the altitude through A is – \(\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\)
Equation of the altitude through A is y – y1 = \(\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\) (x – x1)
(y – y1) (y3 – y2) = -(x – x1) (x3 – x2)
L1 = (x – x1)(x – x3) + (y – y1)(y – y3) = 0.
Similarly equations of the altitudes through B,C are
L2 = (x – x2) (x3 – x1) + (y – y2) (y2 – y3) = 0,
L3 = (x – x3) (x1 – x2) + (y – y3) (y1 – y2) = 0.
Now 1.L1 + 1.L2 + 1.L3 = 0
The altitudes L1 = 0, L2 = 0, L3 = 0 are concurrent.
Theorem:
The internal bisectors of the angles of a triangle are concurrent.
Theorem:
The perpendicular bisectors of the sides of a triangle are concurrent
![]()
Point of Intersection of Two Straight Lines:
Theorem:
The point of intersection of the two non parallel lines
a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 is \(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}, \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)
Proof:
The lines are not parallel ^ Slopes are not equal
⇒ \(\frac{-a_{1}}{b_{1}} \neq \frac{-a_{2}}{b_{2}}\) ⇒ a1b2 ≠ a2b1 ⇒ a1b2 – a2b1 ≠ 0
Let P (α, β) be the point of intersection. Then a1 α + b1β + C1 = 0 and a2 α + b2β + c2 = 0.
Solving by the method of cross multiplication
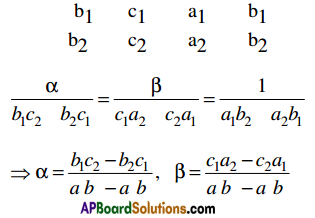
Point of intersection is P = \(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}, \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)
Theorem:
The ratio in which the line L = ax + by + c = 0 divides the line segment joining A(x1, y1), B(x2, y2) is -L11 : L22, where L11 = L(x1, y1) = ax1 + by1 + c and L22 = L(x2, y2) = ax2 + by2 + c.
Proof:
Let k : 1 be the ratio in which the line divides the line segment.
The point which divides in the ratio k : 1 is P = \(\left(\frac{k x_{2}+x_{1}}{k+1}, \frac{k y_{2}+y_{1}}{k+1}\right)\)
Since P lies on the line ax + by + c = 0 ⇒ a\(\left(\frac{k x_{2}+x_{1}}{k+1}\right)\) + b\(\left(\frac{k y_{2}+y_{1}}{k+1}\right)\) + c = 0
⇒ a(kx2 + x1) + b(ky2 + y1) + c(k + 1) = 0
⇒ k(ax2 + by2 + c) = -(ax1 + by1 + c)
⇒ k = –\(\frac{\left(a x_{1}+b y_{1}+c\right)}{a x_{2}+b y_{2}+c}\)
Required Ratio = -(ax1 + by1 + c) : (ax2 + by2 + c)
= -L11: L22.
Note:
The points A,B lie in the same side or opposite side of the line L = 0 according as L11, L22 have the same sign or opposite signs.
- The points A,B are opposite sides of the line L = 0 iff L11 and L22 have opposite signs.
- The points A,B are same side of the line L = 0 iff L11 and L22 have same sign.
Concurrent Lines:
Three or more lines are said to be concurrent if they have a point in common. The common point is called the point of concurrence.
Condition for Concurrency of Three Straight Lines:
Theorem:
The condition that the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0, a3x + b3y + c3 = 0 to be concurrent is a3(b1c2 – b2c1) + b3(c1a2 – c2a1) + c3(a1b2 – a2b1) = 0.
Proof:
Suppose the given lines are concurrent.
Let P(α, β) be the point of concurrence.
Then a1 α + b1 β + c1 = 0 ………..(1)
a2 α + b2 β + c2= 0 ………..(2)
a3 α + b3 β + c3= 0 ………….(3)
By solving (1) and (2) we get
α = \(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)
β = \(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\)
Therefore P = \(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}, \frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\)
Substituting P in eq.(3), we get
a3\(\left(\frac{b_{1} c_{2}-b_{2} c_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\) + b3\(\left(\frac{c_{1} a_{2}-c_{2} a_{1}}{a_{1} b_{2}-a_{2} b_{1}}\right)\) + c3 = 0
a3(b1c2 – b2c1) + b3(c1a2 – c2a1) + C3 (a1b2 – a2b1) = 0 which is required Condition.
Above condition can be written in a determinant form as \(\left|\begin{array}{lll}
a_{1} & b_{1} & c_{1} \\
a_{2} & b_{2} & c_{2} \\
a_{3} & b_{3} & c_{3}
\end{array}\right|\) = 0
![]()
Problem:
Find the Condition that the lines ax + hy + g = 0, hx + by + f = 0, gx + fy + c = 0 to be Concurrent.
Answer:
Let P be the point of ConCurrenCe
aα + h β + g = 0 …………..(1)
hα + b β + f = 0 ………….(2)
gα + f β + c = 0 …………(3)
solving (1) and (2) we get
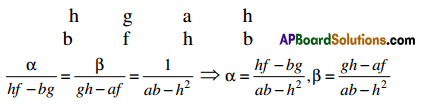
Sub these values in eq.(3)
g\(\left(\frac{h g-b g}{a b-h^{2}}\right)\) + f\(\left(\frac{g h-a f}{a b-h^{2}}\right)\) + c = 0
⇒ g(hf – bg) + f(gh – af) + C(ab – h2) = 0
⇒ fgh – bg2 + fgh – af2 + abc – ch2 = 0
⇒ abc + 2fgh – af2 – bg2 – ch2 = 0
The Condition is abc + 2fgh – af2 – bg2 – ch2 = 0
Family of Straight Lines – Concurrent Straight Lines:
Theorem:
Suppose L1 = a1x + b1y + c1 = 0, L2 = a2x + b2y + c2 = 0 are two intersection lines.
(i) If (λ1, λ2) ≠ (0,0) then λ1L1 + λ2L2 = 0represents a straight line passing through the point of intersection of L1 = 0 and L2 = 0.
(ii) The equation of any line passing through the point of intersection of
L1 = 0, L2 = 0 is of the form where (λ1, λ2) ≠ (0,0).
Note: If L1 = 0, L2 = 0 are two intersecting lines, then the equation of any line other than L2 = 0 passing through their point of intersection can be taken as L1 + λL2 = 0 where λ is a parameter.
Theorem:
If there exists three constants p,q,r not all zero such that
p(a1x + b1y + c1) + q(a2x + b2y + c2) + r(a3x + b3y + c3) = 0 for all x and y then the three lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 and a3x + b3y + c3 = 0 in which no two of them are parallel, are concurrent.
Theorem:
Let L1 = a1x + b1y + c1 = 0, L2 = a2x + b2y + c2 = 0 represent two parallel lines.Then the straight line represented by λ1L1 + λ2L2 = 0 is parallel to each of the straight line L1 = 0 and L2 = 0.
A Sufficient Condition for Concurrency of Three Straight Lines:
Theorem:
If L1 = a1x + b1y + c1 = 0, L2 = a2x + b2y + c2 = 0, L3 = a3x + b3y + c3 = 0 are three straight lines, no two of which are parallel, and
if non-zero real numbers λ1, λ2, λ3 exist such that λ1 L1 + λ2 L2 + λ3 L3 = 0 then the straight lines L1 = 0, L2 = 0 and L3 = 0are concurrent.
![]()
Length of The Perpendicular From A Point to A Straight Line and Distance Between Two Parallel Lines
Theorem:
The perpendicular distance from a point P(x1, y1) to the line ax + by + c = 0 is \(\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
Proof:
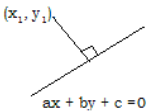
Let the axes be translated to the point P(x1, y1).
Let (X,Y) be the new coordinates of (x, y). Then x = X + x1, y = Y + y1
The transformed equation of the given line is
a(X + x1) + b(Y + y1) + c = 0
⇒ aX + bY + (ax1 + by1 + c) = 0
The perpendicular distance from the new origin P to the line is (from normal form) The perpendicular distance from a point
P(x1, y1) to the line ax+ by + c = 0 is \(\frac{\left|a x_{1}+b y_{1}+c\right|}{\sqrt{a^{2}+b^{2}}}\)
Distance Between Parallel Lines Theorem:
The distance between the two parallel lines ax + by + c1 = 0 and ax + by + c2 = 0 is \(\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
Proof:
Given lines are ax + by + c1 = 0 …………(1)
ax + by + c2 = 0 …………(2)
Let P(x1, y1) be a point on the line (2).
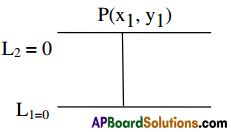
Then
ax1 + by1 + c2 = 0
ax1 + by1 = -c2.
Distance between the parallel lines = Perpendicular distance from P to line (i)
= \(\frac{\left|a x_{1}+b y_{1}+c_{1}\right|}{\sqrt{a^{2}+b^{2}}}=\frac{\left|c_{1}-c_{2}\right|}{\sqrt{a^{2}+b^{2}}}\)
Foot of The Perpendicular:
Theorem:
If (h, k) is the foot of the perpendicular from (x1, y1) to the line ax + by + c = 0 (a0, b0) then \(\frac{h-x_{1}}{a}=\frac{k-y_{1}}{b}=\frac{-\left(a x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\).
Proof:
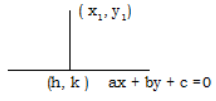
Let A = (x1, y1) P = (h, k)
P lies on ax + by + c = 0
ah + bk + c = 0
ah + bk = – c
Slope of \(\overline{A P}\) is \(\frac{k-y_{1}}{h-x_{1}}\)
Slope of given line is \(-\frac{a}{b}\)
\(\overline{A P}\) is perpendicular to the given line
⇒ \(\left(\frac{k-y_{1}}{h-x_{1}}\right)\left(-\frac{a}{b}\right)\) = -1
⇒ \(\frac{k-y_{1}}{b}=\frac{h-x_{1}}{a}\)
By the law of multipliers in ratio and proportion
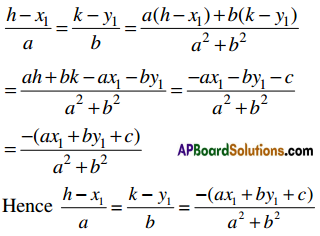
![]()
Image of A Point
Theorem:
If (h, k) is the image of (x1, y1) w.r.t the line ax + by + c = 0 (a ≠ 0, b ≠ 0), then \(\frac{h-x_{1}}{a}=\frac{k-y_{1}}{b}=\frac{-2\left(x_{1}+b y_{1}+c\right)}{a^{2}+b^{2}}\).
Proof:
Let A(x1, y1), B(h, k)
Mid Point of is P = \(\left(\frac{x_{1}+h}{2}, \frac{y_{1}+k}{2}\right)\)
Since B is the image of A,therefore mid point P lies on ax + by + c = 0.
a\(\left(\frac{x_{1}+h}{2}\right)\) + b\(\left(\frac{y_{1}+k}{2}\right)\) + c = 0
⇒ ax1 + by1 + ah + bk + 2c = 0
⇒ ah + bk = -ax1 + by1 – 2c.
Slope of \(\overline{A B}\) is \(\frac{k-y_{1}}{h-x_{1}}\)
Slope of given line is \(-\frac{a}{b}\)
\(\overline{A B}\) is perpendicular to the given line a
⇒ \(\left(\frac{k-y_{1}}{h-x_{1}}\right)\left(-\frac{a}{b}\right)\) = -1
⇒ \(\frac{k-y_{1}}{b}=\frac{h-x_{1}}{a}\)
By the law of multipliers in ratio and proportion
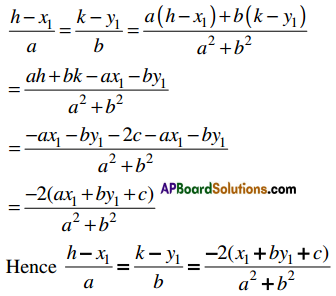
Note :
- The image of (x1, y1) w.r.t the line x = y is (y1, x1)
- The image of (x1, y1) w.r.t the line x + y = 0 is (-y1, -x1)
Theorem:
If the four straight lines ax + by + p = 0, ax + by + q = 0, cx + dy + r = 0 and cx + dy + s = 0 form a parallelogram. Then the area of the parallelogram so formed is
\(\left|\frac{(p-q)(r-s)}{b c-a d}\right|\)
Proof:
Let L1 = ax + by + p = 0
L2 = ax + by + q = 0
L3 = cx + dy + r = 0
L4 = cx + dy + s = 0
Clearly
L1 ∥ L2 and L3 ∥ L4. So L1 and L3 are nonparallel. Let be the angle between L1 and L3.
Let d1 = distance between L1 and L2= \(\frac{|p-q|}{\sqrt{a^{2}+b^{2}}}\)
Let d2 = distance between L3 and L4 = \(\frac{|r-s|}{\sqrt{c^{2}+d^{2}}}\)
Now cos θ = \(\frac{|a c+b d|}{\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\) and sin θ = \(\sqrt{\frac{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)-(a c+b d)^{2}}{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\)
= \(\frac{|b c-a d|}{\sqrt{\left(a^{2}+b^{2}\right)\left(c^{2}+d^{2}\right)}}\)
Now area of the parallelogram is \(\frac{d_{1} d_{2}}{\sin \theta}=\left|\frac{(p-q))(r-s)}{b c-a d}\right|\)
Angle Between Two Lines
Theorem:
If θ is an angle between the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 then
cos θ = ±\(\frac{a_{1} a_{2}+b_{1} b_{2}}{\sqrt{a_{1}^{2}+b_{2}^{3}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
Proof:
The lines passing through the origin and parallel to the given lines are
a1x + b1y = 0, ……… (1)
a2x + b2y = 0. …………….(2)
Let θ1, θ2 be the inclinations of (1) and (2) respectively (θ1 > θ2)
Now θ is an angle between (1) and (2)
θ = θ1 – θ2
P(-b1, a1) satisfies eq(1), the point lies on (1)
Similarly, Q(-b2, a2) lies on (2)
Let L and M be the projection of P, Q respectively on the x – axis.

Note :
- If is the acute angle between the lines then cos θ = \(\frac{\left|a_{1} a_{1}+b_{1} b_{2}\right|}{\sqrt{a_{1}^{2}+b_{1}^{2}} \sqrt{a_{2}^{2}+b_{2}^{2}}}\)
- If is an angle between two lines, then is another angle between the lines.
- If is an angle between two lines are not a right angle then the angle between the lines means the acute angle between the lines.
- If 0 is an angle between the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 then tan θ = \(\frac{a_{1} b_{2}-a_{2} b_{1}}{a_{1} a_{2}+b_{1} b_{2}}\)
- If is the acute angle between the lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 then
tan θ = \(\left|\frac{a_{1} b_{2}-a_{2} b_{1}}{a_{1} a_{2}+b_{1} b_{2}}\right|=\left|\frac{a_{1} / b_{1}-a_{2} / b_{2}}{\left(a_{1} a_{2}\right) /\left(b_{1} b_{2}\right)+1}\right|\)
= \(\left|\frac{\left(-a_{1} / b_{1}\right)-\left(-a_{2} / b_{2}\right)}{1+\left(-a_{1} / b_{1}\right)\left(-a_{2} / b_{2}\right)}\right|\) where mj, m2 are the slopes of the lines.
![]()
Theorem:
The equation of the line parallel to ax + by + c = 0 and passing through (x1, y1) is a(x – x1) + b(y – y1) = 0.
Proof:
Slope of the given line is -a/b.
⇒ Slope of the required line is -a/b.(lines are parallel)
Equation of the required line is
y – y1 = –\(\frac{a}{b}\)(x – x1)
b(y – y1) = -a(x – x1)
a(x – x1) + b(y – y1) = 0.
Note :
- The equation of a line parallel to ax + by + c = 0 may be taken as ax + by + k = 0.
- The equation of a line parallel to ax + by + c = 0 and passing through the origin is ax + by = 0.
Theorem:
The equation of the line perpendicular to ax + by + c = 0 and passing through (x1, y1) is b(x – x1) – a(y – y1) = 0.
Proof:
Slope of the given line is -a/b. ⇒ Slope of the required line is b/a. (since product of slopes = -1)
Equation of the required line is y – y1 = \(\frac{b}{a}\) (x – x1)
a(y – y1) = b(x – x1)
b(x – x1) – a(y – y1) = 0.
Note :
- The equation of a line perpendicular to ax + by + c = 0 may be taken as bx – ay + k = 0
- The equation of a line perpendicular to ax + by + c = 0 and passing through the origin is bx – ay = 0.
Concurrent Lines- Properties Related to A Triangle
Theorem:
The medians of a triangle are concurrent.
Proof:
Let A(x1, y1), B(x2, y2), C(x3, y3) be the vertices of the triangle
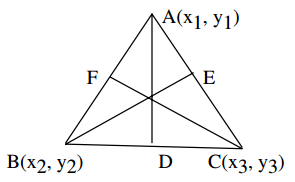
Let D, E, F be the mid points of \(\overline{B C}, \overline{C A}, \overline{A B}\) respectively
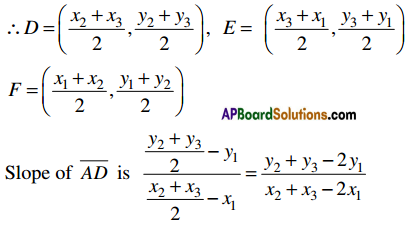
Equation of \(\overline{A D}\)
y – y1 = (x – x1)
(y – y1) (x2 + x3 – 2x1) = (x – x1)(y2 + y3 – 2y1)
⇒ L1 ≡ (x – x1)(y2 + y3 – 2y1) – (y – y1) (x2 + x3 – 2x1) = 0.
Similarly, the equations to \(\overline{B E}\) and \(\overline{C F}\) respectively are L2 ≡ (x – x2)(y3 + y1 – 2y2) – (y – y2) (x3 + x1 – 2x2) = 0.
L3 ≡ (x – x3)(y1 + y2 – 2y3) – (y – y3) (x1 + x2 – 2x3) = 0.
Now 1. L1 + 1.L2 + 1. L3 = 0
The medians L1 = 0, L2 =0, L3 = 0 are concurrent.
Theorem:
The altitudes of a triangle are concurrent.
Proof:
Let A(x1, y1), B(x2, y2), C(x3, y3) be the vertices of the triangle ABC.
Let AD, BE,CF be the altitudes.
Slope of \(\overline{B C}\) is \(\frac{y_{3}-y_{2}}{x_{3}-x_{2}}\) and AD ⊥ BC
Slope of the altitude through A is \(-\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\)
Equation of the altitude through A is y – y1 = \(\frac{x_{3}-x_{2}}{y_{3}-y_{2}}\)(x – x1)
(y – y1) (y3 – y2) = -(x – x1) (x3 – x2)
L1 = (x – x1)(x2 – x3) + (y – y1)(y2 – y3) = 0.
Similarly equations of the altitudes through B,C are
L2 = (x – x2) (x3 – x1) + (y – y2) (y2 – y3) = 0
L3 = (x – x3) (x1 – x2) + (y – y3) (y1 – y2) = 0.
Now 1.L1 + 1.L2 + 1.L3 = 0
The altitudes L1 = 0, L2 =0, L3 = 0 are concurrent.
Theorem:
The internal bisectors of the angles of a triangle are concurrent.
Theorem:
The perpendicular bisectors of the sides of a triangle are concurrent