Students get through Maths 1B Important Questions Inter 1st Year Maths 1B Transformation of Axes Important Questions which are most likely to be asked in the exam.
Intermediate 1st Year Maths 1B Transformation of Axes Important Questions
Question 1.
When the origin is shifted to (2, 3) by the translation of axes, the coordinates of a point p are changed as (4, -3). Find the coordinates of P in the original system.
Solution:
(h, k) = (2, 3) ⇒ h = 2, k = 3
(x’, y’) = (4, 3) ⇒ x = 4, y = -3
x = x’ + h = 4 + 2 = 6, y = y’ + k = -3 + 3 = 0
original Co-ordinates are (6, 0)
![]()
Question 2.
Find the point to which the origin is to be shifted by the translation of axes so as to remove the first-degree terms from the equation
ax2 + 2hxy + by2 + 2gx + 2fy + c = 0, where h2 ≠ ab.
Solution:
Let the origin be shifted to (α, β) by the translation of axes.
Then x = x’ + α,
y = y’ + β
On substituting these in the given equation, we get
a(x’ + α)2 + 2h(x’ + α) (y’ + β) + b(y’ + β)2 + 2g(x’ + α) + 2f(y’ + β) + c = 0
Which gives
ax’2 + 2hx’y’ + by2 + 2x'(α + β + g) + 2y'(hα + bβ + f) + aα2 + 2hαβ + bβ2 + 2gα + 2fβ + c = 0 ……….. (1)
If equation (1) has to be free from the first degree terms, then we have
aα + hβ + g = 0 and hα + bβ +1 = 0
Solving these equations for a and 13, we get
α =\(\frac{h f-b g}{a b-h^{2}}\) , β = \(\frac{g h-a f}{a b-h^{2}}\)
Therefore, the origin is to be shifted to
\(\left(\frac{h f-b g}{a b-h^{2}}, \frac{g h-a f}{a b-h^{2}}\right)\)
Question 3.
Find the point to which the origin is to be shifted by the translation of axes so as to remove the first degree terms from the equation
ax2 + by2 + 2gx + 2fy + c = 0, where a ≠ 0, b ≠ 0.
Solution:
Here the given equation does not contain xy term. Hence writing h = 0 in the result of
Problem 12, the required point is \(\left(\frac{-g}{a}, \frac{-f}{b}\right)\)
![]()
Question 4.
If the point P changes to (4, -3) when the axes are rotated through an angle of 135°, find the coordinates of P with respect to the original system.
Solution:
Here (x’, y’) = (4, -3); θ = 135°
Let (x, y) be the coordinates of P, then
x = x’ cos θ – y’ sin θ
= 4cos 135° – (-3) sin 135°

Therefore, the coordinates of P with respect to the original system are (\(\frac{-1}{\sqrt{2}}\), \(\frac{7}{\sqrt{2}}\))
Question 5.
Show that the axes are to be rotated through an angle of \(\frac{1}{2}\) Tan-1(\(\frac{2 h}{a-b}\)) so as to remove the xy term from the equation ax2 + 2hxy + by2 = 0, if a ≠ b and through the angle \(\frac{\pi}{4}\), if a = b. [Mar 13, 06]
Solution:
If the axes are rotated through an angle ‘θ’,
then
x = x’ cos θ – y’ sin θ
y = x’ sin θ + y’ cos θ
Therefore the given equation transforms as
a(x’ cos θ – y’ sin θ)2 + 2h(x’ cosθ – y’ sinθ) (x’ sinθ + y’ cosθ) + b(x’ sin θ + y’ cos θ)2 = o
To remove x’y’ term from the equation, the coefficient of x’y’ term must be zero.
So, (b – a) sin θ cos θ + h(cos2θ – sin2θ) = 0
i.e., h cos 2θ = \(\frac{a-b}{2}\) sin 2θ
i.e., tan 2θ = \(\frac{2 h}{a-b}\), if a ≠ b and h cos 2θ = 0, if a = b
Therefore θ = \(\frac{1}{2}\) Tan-1(\(\frac{2 h}{a-b}\)), if a ≠ b and θ = \(\frac{\pi}{4}\), If a = b
![]()
Question 6.
When the origin is shifted to (-2, -3) and the axes are rotated through an angle 45° find the transformed equation of 2x2 + 4xy – 5y2 + 20x – 14 = 0.
Solution:
Here (h, k) = (-2, -3), h = -2, k = -3
θ = 45°
Let (x’, y’) be the new co-ordinates of any point (x, y) is the plane after transformation
x = x’ cos θ – y’ sin θ + h = -2 + x’ cos 45° – y’ sin 45°.
= -2 + \(\frac{x^{\prime}-y^{\prime}}{\sqrt{2}}\)
y = x’ si nθ + y’ cos θ + k = x’ sin 45° + y’ cos
45° – 3 = -3 + \(\frac{x^{\prime}+y^{\prime}}{\sqrt{2}}\)
The transformed equation is
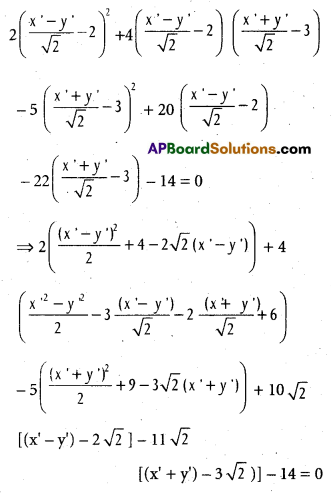
⇒ (x’ – y’)2 + 8 – 4\(\sqrt{2}\) (x’ – y’) + 2(x’2 – y’2) – 6\(\sqrt{2}\) (x’ – y’) – 4\(\sqrt{2}\) (x’ + y’) + 24 = 0
⇒ –\(\frac{5}{2}\) (x’ – y’)2 – 45 + 15\(\sqrt{2}\) (x’ + y’) + 10\(\sqrt{2}\) (x’ – y’) – 40 – 11\(\sqrt{2}\) (x’ + y’) + 66 – 14 = 0
⇒ x’2 + y’2 – 2x’y’ + 2x’2 – 2y’2 – \(\frac{5}{2}\) (x’2 + y’2 + 2x’y’) – 1 = 0
\(\frac{1}{2}\) x’2 – \(\frac{7}{2}\) y’2 – 7x’y’ – 1 = 0
i.e., x’2 – 7y’2 – 14x’y’ – 2 = 0
The transformed equation is (dropping dashes)
x2 – 7y2 – 14xy – 2 = 0
Question 7.
When the origin is shifted to (-2, 3) by translation of axes, let us find the co-ordinates of (1, 2) with respect to new axes.
Solution:
Here (h, k) = (-2, 3)
Let (x, y) = (1, 2) be shifted to (x’ y’) by the translation of axes.
Then (x’, y’) = (x – h, y – k)
= (1 – (-2), 2 – 3) = (3, -1)
![]()
Question 8.
When the origin is shifted to (3, 4) by the translation of axes, let us find the transformed equation of 2x2 + 4xy + 5y2 = 0.
Solution:
Here (h, k) = (3, 4)
on substituting x = x’ + 3 and y = y’ + 4 in the given equation.
as per note the equation f(x, y) = 0 of the curve is transformed as f(x’ + h, y’ + k) = 0]
we get
2(x’ + 3) + 4(x’ + 3) (y’ + 4) + 5(y’ + 4)2 = o
Simplifying this equation, we get
2x’2 + 4x’y’ + 5y’2 + 28x’ + 52y’ + 146 = 0
This equation can be written (dropping dashes) as
2x2 + 4xy + 5y2 + 28x + 52y + 146 = 0