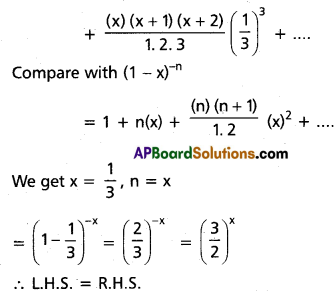Inter 2nd Year Maths 2A Binomial Theorem Solutions Ex 6(b)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Binomial Theorem Solutions Exercise 6(b)

I.

Question 1.
Find the set of values of x for which the binomial expansions of the following are valid.
(i) (2 + 3x)^-2/3
(ii) (5 + x)^3/2
(iii) (7 + 3x)^-5
(iv) \(\left(4-\frac{x}{3}\right)^{-1 / 2}\)
Solution:
(i) (2 + 3x)^-2/3 = \(\left[2\left(1+\frac{3}{2} x\right)\right]^{-2 / 3}\)

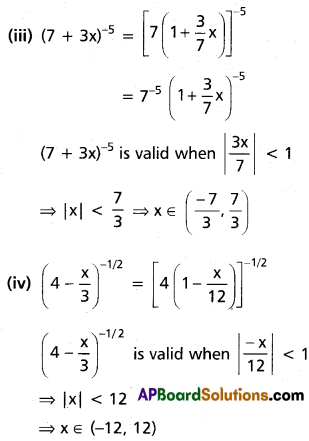
Question 2.
Find the
(i) 6th term of \(\left(1+\frac{x}{2}\right)^{-5}\)
Solution:

(ii) 7th term of \(\left(1-\frac{x^2}{3}\right)^{-4}\)
Solution:

(iii) 10th term of (3 – 4x)^-2/3
Solution:

(iv) 5th term of \(\left(7+\frac{8 y}{3}\right)^{7 / 4}\)
Solution:

Question 3.
Write down the first 3 terms in the expansion of
(i) (3 + 5x)^-7/3
Solution:

(ii) (1 + 4x)^-4
Solution:

(iii) (8 – 5x)^2/3
Solution:

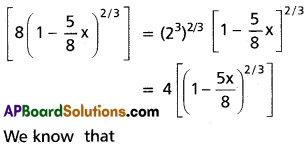
(iv) (2 – 7x)^-3/4
Solution:

Question 4.
Find the general term (r + 1)^th term in the expansion of
(i) (4 + 5x)^-3/2
Solution:

(ii) \(\left(1-\frac{5 x}{3}\right)^{-3}\)
Solution:

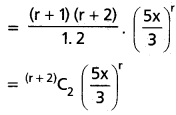
(iii) \(\left(1+\frac{4 x}{5}\right)^{5 / 2}\)
Solution:

(iv) \(\left(3-\frac{5 x}{4}\right)^{-1 / 2}\)
Solution:

II.

Question 1.
Find the coefficient of x¹⁰ in the expansion of \(\frac{1+2 x}{(1-2 x)^2}\)
Solution:

Question 2.
Find the coefficient of x⁴ in the expansion of (1 – 4x)^-3/5
Solution:

Question 3.
(i) Find the coefficient of x⁵ in \(\frac{(1-3 x)^2}{(3-x)^{3 / 2}}\)
Solution:

(ii) Find the coefficient of x⁸ in \(\frac{(1+x)^2}{\left(1-\frac{2}{3} x\right)^3}\)
Solution:

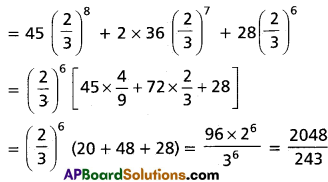
(iii) Find the coefficient of x⁷ in \(\frac{(2+3 x)^3}{(1-3 x)^4}\)
Solution:

Question 4.
Find the coefficient of x³ in the expansion of \(\frac{\left(1+3 x^2\right)^{3 / 2}}{(3+4 x)^{1 / 3}}\)
Solution:

III.

Question 1.
Find the sum of the infinite series
(i) \(1+\frac{1}{3}+\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\ldots\)
Solution:

(ii) \(1-\frac{4}{5}+\frac{4.7}{5.10}-\frac{4.7 .10}{5.10 .15}+\ldots \ldots\)
Solution:

(iii) \(\frac{3}{4}+\frac{3.5}{4.8}+\frac{3.5 .7}{4.8 .12}+\ldots\)
Solution:

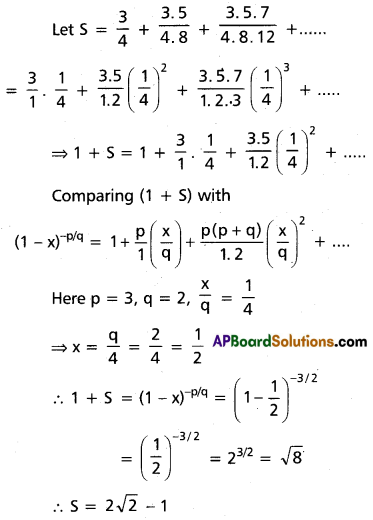
(iv) \(\frac{3}{4.8}-\frac{3.5}{4.8 .12}+\frac{3.5 .7}{4.8 .12 .16}-\ldots \ldots\)
Solution:

Question 2.
If t = \(\frac{4}{5}+\frac{4.6}{5.10}+\frac{4.6 .8}{5.10 .15}+\ldots \ldots \ldots \infty\), then prove that 9t = 16.
Solution:

Question 3.
If x = \(\frac{1.3}{3.6}+\frac{1.3 .5}{3.6 .9}+\frac{1.3 .5 .7}{3.6 .9 .12}+\ldots \ldots\) then prove that 9x² + 24x = 11.
Solution:

⇒ 3x + 4 = 3√3
Squaring on both sides
(3x + 4)² = (3√3)²
⇒ 9x² + 24x + 16 = 27
⇒ 9x² + 24x = 11

Question 4.
If x = \(\frac{5}{(2 !) \cdot 3}+\frac{5 \cdot 7}{(3 !) \cdot 3^2}+\frac{5 \cdot 7 \cdot 9}{(4 !) \cdot 3^3}+\ldots\) then find the value of x² + 4x.
Solution:

Question 5.
Find the sum of the infinite series \(\frac{7}{5}\left(1+\frac{1}{10^2}+\frac{1.3}{1.2} \cdot \frac{1}{10^4}+\frac{1.3 .5}{1.2 .3} \cdot \frac{1}{10^6}+\ldots .\right)\)
Solution:

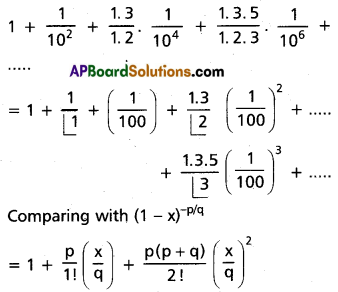
Question 6.
Show that \(1+\frac{x}{2}+\frac{x(x-1)}{2.4}+\frac{x(x-1)(x-2)}{2.4 .6}+\ldots .\) = \(1+\frac{x}{3}+\frac{x(x+1)}{3.6}+\frac{x(x+1)(x+2)}{3.6 .9}+\ldots\)
Solution: