Inter 2nd Year Maths 2A Partial Fractions Solutions Ex 7(b)

Practicing the Intermediate 2nd Year Maths 2A Textbook Solutions Inter 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2A Partial Fractions Solutions Exercise 7(b)

Resolve the following into partial fractions.

Question 1.
\(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}\)
Solution:
Let \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{A}{x-1}+\frac{B x+C}{x^2+2}\)
Multiplying with (x – 1) (x² + 2)
2x² + 3x + 4 = A(x² + 2) + (Bx + C) (x – 1)
x = 1
⇒ 2 + 3 + 4 = A(1 + 2)
⇒ 9 = 3A
⇒ A = 3
Equating the coefficients of x²
2 = A + B
⇒ B = 2 – A = 2 – 3 = -1
Equating constants
4 = 2A – C
⇒ C = 2A – 4 = 6 – 4 = 2
∴ \(\frac{2 x^2+3 x+4}{(x-1)\left(x^2+2\right)}=\frac{3}{x-1}+\frac{-x+2}{x^2+2}\)

Question 2.
\(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}\)
Solution:
Let \(\frac{3 x-1}{\left(1-x+x^2\right)(x+2)}=\frac{A}{2+x}+\frac{B x+C}{1-x+x^2}\)
Multiplying with (2 + x) (1 – x + x²)
3x – 1 = A(1 – x + x²) (Bx + C) (2 + x)
x = -2
⇒ -7 = A(1 + 2 + 4) = 7A
⇒ A = -1
Equating the coefficients of x²
0 = A + B ⇒ B = -A = 1
Equating the constants
-1 = A + 2C
⇒ 2C = -1 – A = -1 + 1 = 0
⇒ C = 0
∴ \(\frac{3 x-1}{\left(1-x+x^2\right)(2+x)}=-\frac{1}{2+x}+\frac{x}{1-x+x^2}\)

Question 3.
\(\frac{x^2-3}{(x+2)\left(x^2+1\right)}\)
Solution:
Let \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{A}{x+2}+\frac{B x+C}{x^2+1}\)
Multiplying with (x + 2) (x² + 1)
x² – 3 = A(x² + 1) + (Bx + C) (x + 2)
x = -2
⇒ 4 – 3 = A(4 + 1)
⇒ 1 = 5A
⇒ A = \(\frac{1}{5}\)
Equating the coefficients of x²
1 = A + B
⇒ B = 1 – A = 1 – \(\frac{1}{5}\) = \(\frac{4}{5}\)
Equating the constants
-3 = A + 2C
⇒ 2C = -3 – A
⇒ 2C = -3 – \(\frac{1}{5}\)
⇒ 2C = \(-\frac{16}{5}\)
⇒ C = \(-\frac{8}{5}\)
∴ \(\frac{x^2-3}{(x+2)\left(x^2+1\right)}=\frac{1}{5(x+2)}+\frac{4 x-8}{5\left(x^2+1\right)}\)

Question 4.
\(\frac{x^2+1}{\left(x^2+x+1\right)^2}\)
Solution:
Let \(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{A x+B}{x^2+x+1}+\frac{C x+D}{\left(x^2+x+1\right)^2}\)
Multiplying with (x² + x + 1)²
x² + 1 = (Ax + B) (x² + x + 1) + (Cx + D)
Equating the coefficients of x³,
A = 0
Equating the coefficients of x²,
A + B = 1 ⇒ B = 1
Equating the coefficients of x,
A + B + C = 0
⇒ 1 + C = 0
⇒ C = -1
Equating the constants,
B + D = 1
⇒ D = 1 – B = 1 – 1 = 0
∴ Ax + B = 1, Cx + D = -x
∴ \(\frac{x^2+1}{\left(x^2+x+1\right)^2}=\frac{1}{x^2+x+1}-\frac{x}{\left(x^2+x+1\right)^2}\)

Question 5.
\(\frac{x^3+x^2+1}{(x-1)\left(x^3-1\right)}\)
Solution:

∴ x³ + x² + 1 = A(x – 1) (x² + x + 1) + B(x² + x + 1) + (Cx + D) (x – 1)² …….(2)
Put x = 1 in (2)
1 + 1 + 1 = A(0) + B(1 + 1 + 1) + (C(1) + D) (0)
⇒ 3B = 3
⇒ B = 1
Equating the coefficients of x³ in (2)
1 = A + C ………(3)
Equating the coefficients of x² in (2)
1 = A(1 – 1) + B(1) + C(-2) + D(1)
⇒ 1 = B – 2C + D
∵ B = 1,
⇒ 1 = 1 – 2C + D
⇒ 2C = D ………(4)
Put x = 0 in (2)
1 = A(-1)(1) + B(1) + D(-1)²
⇒ -A + B + D = 1
⇒ -A + 1 + D = 1
⇒ A = D ………(5)
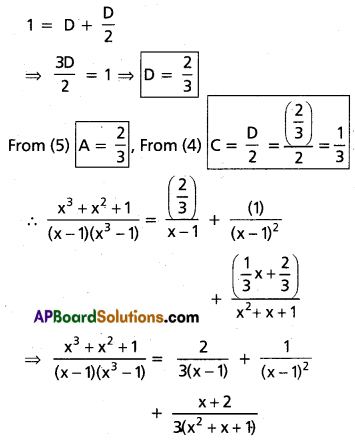
From (3), (4) and (5)