Inter 2nd Year Maths 2B Definite Integrals Solutions Ex 7(c)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(c) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Definite Integrals Solutions Exercise 7(c)

I. Evaluate the following definite integrals.

Question 1.
\(\int_{\pi/2}^{\pi/2}\)sin¹⁰ x dx
Solution:

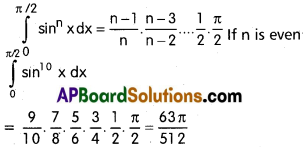
Question 2.
\(\int_0^{\pi/2}\)cos¹¹ x dx
Solution:

Question 3.
\(\int_0^{\pi/2}\)cos⁷ x . sin²x dx.
Solution:

Question 4.
\(\int_0^{\pi/2}\)sin⁴ x . cos⁴ x dx.
Solution:

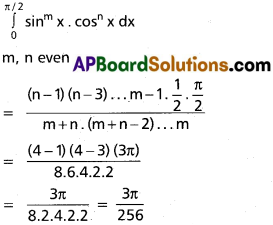
Question 5.
\(\int_0^{\pi/2}\)sin³ x cos⁶ x dx.
Solution:
\(\int_0^{\pi/2}\)sin³ x cos⁶ x dx.
\(\int_0^{\pi/2}\)(1 – cos² x) cos⁶ x.sin x dx

Question 6.
\(\int_0^{2\pi}\)sin² x cos⁴ x dx.
Solution:

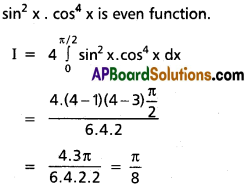
Question 7.
\(\int_{-\pi/2}^{\pi/2}\)sin² θ cos⁷ θ dθ.
Solution:
sin² θ cos⁷ θ is even function
f(θ) = sin² θ . cos⁷ θ dθ
f(-θ) = sin² (-θ) . cos⁷ (-θ)
= f(θ)
= 2\(\int_{-\pi/2}^{\pi/2}\)sin² θ cos⁷ θ dθ

\(\int_0^{\pi/2}\)sin^m x cosⁿx dx
n is odd n = 7

Question 8.
\(\int_{-\pi/2}^{\pi/2}\)sin³ θ .cos³ θ dθ.
Solution:
f(θ) = sin³ θ . cos³ θ dθ
f(-θ) = sin³ (-θ) . cos³ (-θ)
= -sin³ θ cos³ θ = -f(θ)
f(θ) is odd
∴ \(\int_{-\pi/2}^{\pi/2}\)sin³ θ.cos³ θ dθ = 0

Question 9.
\(\int_0^a\)x(a² – x²)^7/2 dx
Solution:
x = a sin θ, a = a sin θ
dx = a cos θ dθ, θ = π/2
= \(\int_0^{\pi/2}\)a sin θ(a² – a²sin²θ)^7/2 a cos θ dθ
= \(\int_0^{\pi/2}\)a⁹ cos⁸ θ sin θ dθ
= a⁹\(\int_0^{\pi/2}\)cos⁸ . θ sin θ dθ

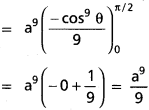
Question 10.
\(\int_0^2\)x^3/2.\(\sqrt{2-x}\)dx
Solution:
x = 2 cos² θ
dx = 4 cos θ sin θ dθ

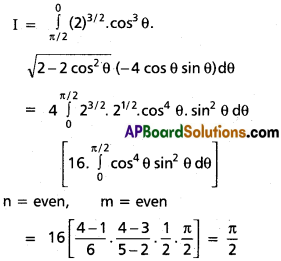
II. Evaluate the following integrals.

Question 1.
\(\int_0^1\)x⁵(1 – x)^3/2 dx
Solution:
x = sin² θ
dx = 2 sin θ . cos θ . dθ

Question 2.
\(\int_0^4\)(16 – x²)^5/2 dx
Solution:

Question 3.
\(\int_{-3}^3\)(9 – x²)^3/2 x dx
Solution:
Let f(x) = (9 – x²)^3/2_x
f(x) = (9 – (-x²))^3/2(-x)
= (9 – x²)^3/2 . x
= -f(x)
∴ f is odd function
∴ \(\int_{-3}^3\)(9 – x²)^3/2 x dx = 0

Question 4.
\(\int_0^5\)x³(25 + x²)^7/2 dx
Solution:
Let I = \(\int_0^5\)x³(25 + x²)^7/2 dx
Put x = 5 sin θ
dx = 5 cosθ dθ

Question 5.
\(\int_{-\pi}^{\pi}\)sin⁸ x cos⁷ x dx
Solution:
Let f(x) = sin⁸ x. cos⁷ x
f(-x) = sin⁸ (-x) . cos⁷ (-x)
= sin⁸ x. cos⁷ x
∴ f is even function.
∴ \(\int_{-\pi}^{\pi}\)sin⁸ x cos⁷ x dx = 2\(\int_0^{\pi}\)sin⁸ x cos⁷ x = 0

Question 6.
\(\int_3^7 \sqrt{\frac{7-x}{x-3}}\)dx
Solution:
Put x = 3 cos²θ + 7 sin²θ
dx = (7 – 3)sin2θ dθ
dx = 4 sin 2θ dθ
U.L.
x = 3 cos²θ + 7 sin²θ
7 = 3 cos²θ + 7 sin²θ
4 cos²θ = 0
θ = \(\frac{\pi}{2}\)
L.L
x = 3 cos²θ + 7 sin²θ
3 = 3 sin²θ + 7 sin²θ
4 sin²θ = 0
sinθ = 0
θ = 0
7 – x = 7 – (3 cos²θ + 7 sin²θ)
= (7 – 3)cos²θ
= 4 cos²θ
x – 3 = 3 cos²θ + 7 sin²θ – 3
= (7 – 3)sin²θ
= 4 sin²θ

Question 7.
\(\int_2^6\sqrt{(6-x)(x-2)}\)dx
Solution:
Put x = 2 cos²θ + 6 sin²θ
dx = (6 – 2) sin2θ dθ
dx = 4 sin2θ dθ
U.L
x = 2 cos²θ + 6 sin²θ
6 = 2 cos²θ + 6 sin²θ
4 cos²θ = 0
cos θ = 0
θ = \(\frac{\pi}{2}\)

L.L
x = 2 cos²θ + 6 sin²θ
2 = 2 cos²θ + 6 sin²θ
4 sin²θ = 0
θ = 0
6 – x = 6 – (2 cos²θ + 6 sin²θ)
= (6 – 2) cos²θ
= 4 cos²θ
x – 2 = 2 cos²θ + 6 sin²θ – 2
= (6 – 2)sin²θ
= 4 sin²θ

Question 8.
\(\int_0^{\pi}\)tan⁵x cos⁸x dx
Solution:

III. Evaluate the following integrals.

Question 1.
\(\int_0^1\)x^7/2 (1 – x)^5/2 dx
Solution:
Put x = sin²θ
dx = 2 sin θ cos θ dθ
U.L
x = sin²θ
1 = sin²θ
θ = \(\frac{\pi}{2}\)

L.L
x = sin²θ
0 = sin²θ
θ = 0

Question 2.
\(\int_0^{\pi}\)(1 + cos x)³ dx
Solution:

Question 3.
\(\int_4^9\frac{dx}{\sqrt{(9 – x)(x – 4)}}\)
Solution:
Put x = 4 cos²θ + 9 sin²θ
dx = (9 – 4)sin2θ dθ
dx = 5 sin2θ dθ

U.L
x = 4 cos²θ + 9 sin²θ
9 = 4 cos²θ + 9 sin²θ
5 cos²θ = 0
θ = \(\frac{\pi}{2}\)

L.L
x = 4 cos²θ + 9 sin²θ
4 = 4 cos²θ + 9 sin²θ
5 sin²θ = 0
θ = 0

9 – x = 9 – (4 cos²θ + 9 sin²θ)
= (9 – 4) cos²θ
= 5 cos²θ

x – 4 = 4 cos²θ + 9 sin²θ – 4
= (9 – 4) sin²θ
= 5 sin²θ

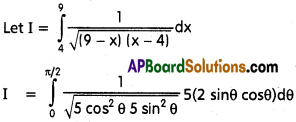
Question 4.
\(\int_0^5\)x²(\(\sqrt{5-x}^7\) dx
Solution:
Put x = 5 sin²θ
dx = 10 sinθ cosθ dθ

U.L
x = 5 sin²θ
5 = 5 sin²θ
sin²θ = 1
θ = \(\frac{\pi}{2}\)

L.L
x = 5 sin²θ
0 = 5sin²θ
sin²θ = 0
θ = 0

Question 5.
\(\int_0^{2\pi}\)(1 + cos x)⁵(1 – cos x)³ dx.
Solution:
\(\int_0^{2\pi}\)(1 + cos x)⁵(1 – cos x)³ dx . (1 + cos x)³(1 + cos x)²(1 – cos x)³