Inter 2nd Year Maths 2B Differential Equations Solutions Ex 8(b)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Differential Equations Solutions Exercise 8(b)

I.

Question 1.
Find the general solution of \(\sqrt{1-x^2}\) dy + \(\sqrt{1-y^2}\) dx = 0.
Solution:
Given differential equation is

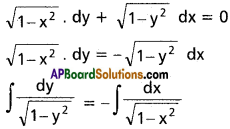
sin^-1 y = – sin^-1 x + c
Solution is sin^-1 x + sin^-1 y = c, where c is a constant.

Question 2.
Find the general solution of \(\frac{dy}{dx}=\frac{2y}{x}\).
Solution:
\(\frac{dy}{dx}=\frac{2y}{x}\)
∫\(\frac{dy}{dx}\) = 2∫\(\frac{2y}{x}\)
log c + log y = 2 log x
log cy = log x²
Solution is cy = x², where c. is a constant.

II. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{1+y^2}{1+x^2}\)
Solution:
\(\frac{dy}{dx}=\frac{1+y^2}{1+x^2}\)
∫\(\frac{dy}{1+y^2}\) = ∫\(\frac{dx}{1+x^2}\)
tan^-1 y = tan^-1 x + tan^-1c where c is a constant.

Question 2.
\(\frac{dy}{dx}\) = e^y-k
Solution:
\(\frac{dy}{dx}=\frac{e^y}{e^x}\)
\(\frac{dy}{e^y}=\frac{dx}{e^x}\)
∫e^-xdx = ∫e^-ydy
-e^-x = -e^-y + C
e^-y = e^-x + c where c is a constant.

Question 3.
(e^x + 1) y dy + (y + 1) dx = 0
Solution:
(e^x + 1 )y. dy = – (y + 1) dx

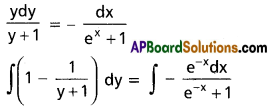
y – log (y + 1) = log (e^-x + 1) + log c
⇒ y – log (y + 1) = log c (e^-x + 1)
⇒ y = log (y + 1) + log c (e^-x + 1)
y = log c (y + 1) (e^-x +1)
Solution is
e^y = c(y + 1) (e^-x +1)

Question 4.
\(\frac{dy}{dx}\) = e^x-y + x²e^-y
Solution:
\(\frac{dy}{dx}\) = e^x-y + x² . e^-y
= \(\frac{e^x}{e^y}=\frac{x^2}{e^y}\)
∫e^y . dy = ∫(e^x + x²) dx
Solution is
e^y = e^x + \(\frac{x^3}{3}\) + c

Question 5.
tan y dx + tan x dy = 0
Solution:
tan y dx = – tan x dy

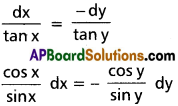
log sin x = – log sin y + log c
log sin x + log sin y = log c
log (sin x . sin y) = log c
⇒ sin x . sin y = c is the solution

Question 6.
\(\sqrt{1+x^2}\)dx + \(\sqrt{1+y^2}\)dy = 0
Solution:
\(\sqrt{1+x^2}\)dx = –\(\sqrt{1+y^2}\)dy
Integrating both sides we get
∫\(\sqrt{1+x^2}\)dx = -∫\(\sqrt{1+y^2}\)dy
Integrating both sides we get

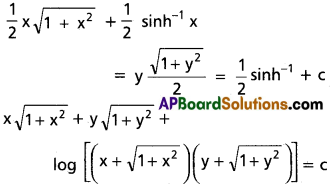
Question 7.
y – x\(\frac{dy}{dx}\) = 5(y² + \(\frac{dy}{dx}\))
Solution:
y – 5y² = (x + 5)\(\frac{dy}{dx}\)
\(\frac{dx}{x+5}=\frac{dy}{y(1-5y}\)
Integrating both sides

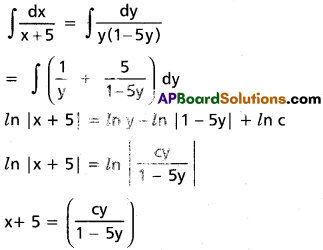
Question 8.
\(\frac{dy}{dx}=\frac{xy+y}{xy+x}\)
Solution:

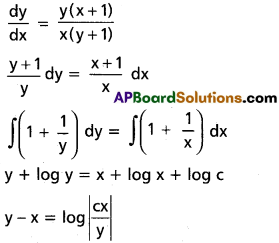
III. Solve the following differential equations.

Question 1.
\(\frac{dy}{dx}=\frac{1+y^2}{(1+x^2)xy}\)
Solution:

log (1 + y²) = log x² – log (1 + x²) + log c
log (1 + x²) + log (1 + y²) = log x² + log c
Solution is (1 + x²) (1 + y²) = cx²

Question 2.
\(\frac{dy}{dx}\) + x² = x² e^3y
Solution:

log(1 – e^-3y) = x³ + c'(c’ = 3c)
Solution is
1 – e^-3y = e^x³ . k(k = e^c’)

Question 3.
(xy² + x)dx+(yx²+y)dy = 0.
Solution:
(xy² + x) dx + (yx² + y) dy = 0
x(y² + 1) dx + y (x² + 1) dy = 0
Dividing with (1 + x²) (1 + y²)
\(\frac{x dx}{1+x^2}+\frac{y dy}{1+y^2}\) = 0
Integrating
∫\(\frac{x dx}{1+x^2}\) + ∫\(\frac{y dy}{1+y^2}\) = 0
\(\frac{1}{2}\) [(log (1 + x²) + log (1 + y²)] = log c
log (1 + x²) (1 + y²) = 2 log c = log c²
Solution is (1 + x²) (1 + y²) = k when k = c².

Question 4.
\(\frac{dy}{dx}\) = 2y tanh x
Solution:
\(\frac{dy}{dx}\) = 2y tanh x
\(\frac{dy}{y}\) = 2 tanh x dx
Integrating both sides we get
∫\(\frac{dy}{y}\) = 2 ∫ tanh x dx
log y = 2 log |cosh x| + log c
lny = 2ln cosh x + In c
y = c cos²h x

Question 5.
sin^-1 \(\frac{dy}{dx}\) = x + y
Solution:
\(\frac{dy}{dx}\) = sin(x + y)
x + y = t
1 + \(\frac{dy}{dx}=\frac{dt}{dx}\)
\(\frac{dt}{dx}\) – 1 = sin t
\(\frac{dt}{dx}\) = 1 + sin t
Integrating both sides we get
∫\(\frac{dt}{1+\sin t}\) = ∫dx
∫\(\frac{1-\sin t}{\cos^2 t}\) dt = x + c
∫sec² t dt – ∫tan t . sec t dt = x + c
tan t – sec t = x + c
⇒ tan (x + y) – sec (x + y) = x + c

Question 6.
\(\frac{dy}{dx}+\frac{y^2+y+1}{x^2+x+1}\) = 0
Solution:
\(\frac{-dy}{y^2+y+1}=\frac{dx}{x^2+x+1}\)
Integrating both sides dy

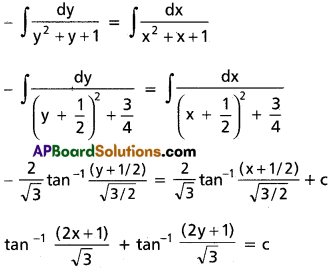
Question 7.
\(\frac{dy}{dx}\) = tan² (x + y)
Solution:
\(\frac{dy}{dx}\) = tan² (x + y)
put v = x + y

2v + sin 2v = 4x + c’
2(x + y) + sin 2(x + y) = 4x + c’
x – y – \(\frac{1}{2}\)sin [2(x + y)] = c