Inter 2nd Year Maths 2B Ellipse Important Questions

Students get through Maths 2B Important Questions Inter 2nd Year Maths 2B Ellipse Important Questions which are most likely to be asked in the exam.

Intermediate 2nd Year Maths 2B Ellipse Important Questions

Question 1.
Find the value of k if 4x + y + k = 0 is a tangent to the ellipse x² + 3y² = 3. [AP Mar. 16, 15]
Solution:
Equation of the ellipse is
x² + 3y² = 3
\(\frac{x^{2}}{3}\) + \(\frac{y^{2}}{1}\) = 1
a² =, 3, b² = 1
Equation of the line is 4x + y + k = 0
y = -4x – k .
m = -4c = -k.
Condition for tangency is c² = a²m² + b²
(-k)² = 3 (4)² + 1 ,
k² = 48 + 1 = 49
k = ±7.

Question 2.
Find the equation of tangents to the ellipse 2x² + y² = 8 which are
i) Parallel to x – 2y – 4 = 0 [May. 05, Mar. 06] [T.S. Mar. 17]
Solution:
Slope will be : \(\frac{1}{2}\)
Equation of tangent y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
y = \(\frac{1}{2}\)x ± \(\sqrt{a^{2}\left(\frac{1}{2}\right)^{2}+b^{2}}\)
\(\frac{x^{2}}{4}\) + \(\frac{y^{2}}{8}\) = 1
y = \(\frac{1}{2}\)x ± \(\sqrt{4 \times \frac{1}{4}+8}\)
y = \(\frac{1}{2}\)x ± 3
2y – x ± 6 = 0 required equation of tangents.
x – 2y ± 6 = 0.

Question 3.
Find the equation of the ellipse in the standard form whose distance between foci is 2 and the length of latus rectum is \(\frac{1}{2}\). [T.S. Mar. 15]
Solution:
Latus rectum = \(\frac{15}{2}\)
distance between foci = 2
\(\frac{2 b^{2}}{a}\) = \(\frac{15}{2}\) ; 2ae = 2
ae = 1
⇒ b² = a² – a² e²
⇒ b² = a² – 1
⇒ \(\frac{15}{4}\)a = a² – 1 .
⇒ 4a² – 15a – 4 = 0
a = 4 or a = –\(\frac{1}{4}\)
b² = a² – 1
= 16 – 1
Equation of the ellipse is \(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{15}\) = 1

Question 4.
Find the equation of the ellipse in the standard form such that distance between foci is 8 and distance between directrices is 32. [Mar. 06, May. 07]
Solution:
Distance between foci = 8.
Distance between directrices = 32
2ae = 8
ae = 4
\(\frac{2 a}{e}\) = 32
\(\frac{a}{e}\) = 16
(ae) (\(\frac{a}{e}\)) = 64
a² = 64
b² = a² – a² e²
= 64 – 16 = 48
Equation of the ellipse is
∴ \(\frac{x^{2}}{64}\) + \(\frac{y^{2}}{48}\) = 1

Question 5.
Find the condition for the line x cos α + y sin α = p to be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1. [Mar. 14]
Solution:
Equation of the ellipse is

Question 6.
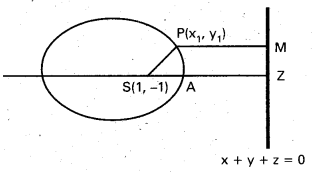
Find the equation of the ellipse with focus at (1, -1) e = \(\frac{2}{3}\) and directrix as x + y + 2 = 0. [Mar. 05] [T.S. Mar. 19]
Solution:
P(x₁, y₁) is any point on the ellipse. Equation of the directrix is
x + y + 2 = 0
Draw PM perpendicular to ZM, Join SP
By Definition of ellipse SP = e. PM
SP² = e² . PM²
(x₁ – 1)² + (y₁ + 1)² (\(\frac{2}{3}\))²[latex]\frac{x_{1}+y_{1}+2}{\sqrt{1+1}}[/latex]²
(x₁ – 1)² + (y₁+ 1)² = \(\frac{4}{9} \frac{\left(x_{1}+y_{1}+2\right)^{2}}{2}\)
9[(x₁ – 1)² + (y₁ + 1)²] = 2 (x₁ + y₁ + 2]²
9[x₁² – 2x₁ + 1 + y₁² + 2y₁ + 1] = 2[x₁² + y₁² + 4 + 2x₁y₁ + 4x₁ + 4y₁]
9x₁² + 9y₁² – 18x₁ + 18y₁ + 18 = 2x₁² + 2y₁² + 4x₁y₁ + 8x₁ + 8y₁ + 8
7x₁² – 4x₁y₁ + 7y₁² – 26x₁ + 10y₁ + 10 = 0
focus of P (x₁, y₁) is 7x² – 4xy + 7y² – 26x + 10y + 10 = 0
This is the equation of the required Ellipse.

Question 7.
L Find tle length of major axis, minor axis, latus rectum, eccentricity, co-ordinates of centre, foci and the equations of directrices of the following ellipse. [TS Mar. 16; Mar. 14]
i) 9x² + 16y² = 144
ii) 4x² + y² – 8x + 2y + 1 = 0
iii) x² + 2y² – 4x + 12y + 14 = 0 [Mar. 11, May 07]
Solution:
Given equation is 9x² + 16y² = 144
\(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{9}\) = 1
∴ a = 4, b = 3
Length of major axis = 2a = 2 . 4 = 8
Length of minor axis = 2b = 2 . 3 = 6
Length of latus rectum = \(\frac{2 b^{2}}{a}\) = \(\frac{2.9}{4}\) = \(\frac{9}{2}\)
Eccentricity = \(\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}=\sqrt{\frac{16-9}{16}}=\frac{\sqrt{7}}{4}\)
Centre is C (0, 0)
Foci are (± ae, 0) = ( ± \(\sqrt{7}\), 0)
Equations of the directrices are x = ± \(\frac{a}{e}\)
x = ± 4 . \(\frac{4}{\sqrt{7}}\) = ± \(\frac{16}{\sqrt{7}}\)
\(\sqrt{7}\)x = ± 16

(ii) Given equation is 4x² + y² – 8x + 2y + 1 = 0
4(x² – 2x) + (y² + 2y) = – 1
4(x – 1)² + (y + 1)² = 4 + 1 – 1 = 4
\(\frac{(x-1)^{2}}{1}\) + \(\frac{(y+1)^{2}}{4}\) = 1
Hence a < b ⇒ y – axis is major axis
a = 1, b = 2
Length of major axis = 2b = 4
Length of minor axis = 2a = 2
Length of lattis rectum = \(\frac{2 a^{2}}{b}\) = \(\frac{2}{2}\) = 1
Eccentricity = \(\sqrt{\frac{b^{2}-a^{2}}{b^{2}}}=\sqrt{\frac{4-1}{4}}=\frac{\sqrt{3}}{2}\)
Centre is C (-1, 1)
be = 2 . \(\frac{\sqrt{3}}{2}\) = \(\sqrt{3}\)
Foci are (-1, 1 ± \(\sqrt{3}\))
Equations of the directrices are y + 1 = ± \(\frac{b}{e}\)
= ± \(\frac{4}{\sqrt{3}}\)
\(\sqrt{3}\) y + \(\sqrt{3}\) = ± 4
\(\sqrt{3}\) y + \(\sqrt{3}\) ± 4 = 0

iii) Given equation is x² + 2y² – 4x + 12y + 14 = 0
x² – 4x + 2 (y² + 6y) = 14
⇒ (x² – 4x + 4) + 2(y² + 6y + 9) = 4 + 18 – 14
⇒ (x – 2)² + 2(y + 3)² = 8
⇒ \(\frac{(x-2)^{2}}{8}\) + \(\frac{(y+3)^{2}}{4}\) = 1
⇒ \(\frac{(x-2)^{2}}{(2 \sqrt{2})^{2}}\) + \(\frac{(y+3)^{2}}{2^{2}}\) = 1
a = 2\(\sqrt{2}\), b = 2, h = 2, k = -3
Length of major axis = 2a = 2(2 \(\sqrt{2}\)) = 4 \(\sqrt{2}\)
Length of minor axis = 2b = 2(2) = 4
Length of latus rectum
= \(\frac{2 \mathrm{~b}^{2}}{\mathrm{a}}\) = \(\frac{2(4)}{2 \sqrt{2}}\) = 2\(\sqrt{2}\)
Eccentricity = \(\sqrt{1-\frac{b^{2}}{a^{2}}}=\sqrt{1-\frac{4}{8}}=\frac{1}{\sqrt{2}}\)
Centre = (h, k) = (2,-3)
Foci = (h ± ae, k) = (2 ± 2, -3)
= (4, -3), (0, -3)
Equations of the directrices are x – h = ± \(\frac{a}{e}\)
x – 2 = \(\frac{2 \sqrt{2}}{\left(\frac{1}{\sqrt{2}}\right)}\)
x – 2 = ± 4
i.e., x = 6, x = -2.

Question 8.
Find the equations of tangent and normal to the ellipse 2x² + 3y² = 11 at the point whose ordinate is 1. [T.S. Mar. 16]
Solution:
Equation of the ellipse is 2x² + 3y² = 11
Given y = 1
2x² + 3 = 11
⇒ 2x² = 8
x² = 4
x = ±2
Points on the ellipse are P (2, 1) and Q(-2, 1)
Case i) P (2, 1)
Equation of the tangent is 2x . 2 + 3y . 1 = 11
4x + 3y = 11
The normal is perpendicular to the tangent Equation of the normal at P can be taken as
3x – 4y = k
The normal passes through p (2, 1)
6 – 4 = k ⇒ k = 2
Equation of the normal at P is 3x – 4y = 2.
Case ii) Q (-2, 1)
Equation of the tangent at Q is
2x(-2) + 3y . 1 = 11
-4x + 3y =1 1
4x – 3y + 11 = 0
Equation of the normal can be taken as
3x + 4y = k
The normal passes through Q (-2, 1)
-6 + 4 = k ⇒ k = -2
Equation of the normal at Q is 3x + 4y = -2
or 3x + 4y + 2 = 0.

Question 9.
Find the eccentricity, co-ordinates of foci. Length of latus rectum and equations of directrices of the following ellipses.
i) 9x² + 16y² – 36x + 32y – 92 = 0,
ii) 3x² + y² – 6x – 2y – 5 = 0 [T.S. Mar. 15]
Solution:
i) Given ellipse is
9x² + 16y² – 36x + 32y – 92 = 0
9(x² – 4x + 4) + 16 (y² + 2y + 1)
= 92 + 36 + 16
9(x – 2)² + 16(y + 1)² = 144
comparing with \(\frac{(x-2)^{2}}{16}\) + \(\frac{(y+1)^{2}}{9}\) = 1,
we get
a² = 16, b² = 9 ⇒ a = 4, b = 3.

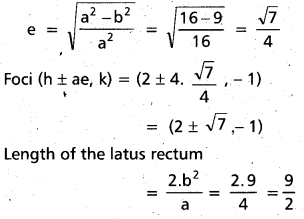
Equations of the directrices are x = h ± \(\frac{\mathrm{a}}{\mathrm{e}}\)
x = 2 ± \(\frac{4 \times 4}{\sqrt{7}}\)
\(\sqrt{7x}\) = 2\(\sqrt{7}\) ± 16

ii) 3x² + y² – 6x – 2y – 5 = 0
Solution:
3(x² – 2x) + (y² – 2y) = 5
⇒ 3(x² – 2x + 1) + (y² – 2y + 1) = 9
⇒ 3(x – 1)² + (y – 1)² = 9
comparing with ⇒ \(\frac{(x-1)^{2}}{3}\) + \(\frac{(y-1)^{2}}{9}\) = 1,
we get
a < b ⇒ Y – axis is the major axis
a² = 3, b² = 9
a = \(\sqrt{3}\), b = 3, h = 1, k = 1
Length of major axis = 2b = 2(3) = 6
Length of minor axis = 2a = 2\(\sqrt{3}\)

Question 10.
Find the equation of the tangent and normal to the ellipse 9x² + 16y² = 144 at the end of the latus rectum in the first quadrant. [A.P. Mar. 15, Mar. 07]
Solution:
Given ellipse is 9x² + 16y² = 144

Equation of the normal at P is

Question 11.
Show that the points of intersection of the perpendicular tangents to an ellipse lie on a circle. [A.P. Mar. 16]
Solution:
Let the equation of the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
(a > b). Any tangent to it in the slope-intercept form is y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) …………………. (1)
Let the perpendicular tangents intersect at P(x₁, y₁).
∴ P lies on (1) for some real m, i.e.,
y₁ = mx₁ ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
∴ (y₁ – mx₁)² = a²m² + b².
or .
(x₁² – a²) m² – 2x₁y₁m + (y₁² – b²) = 0 being a
quadratic equation in ‘m’ has two roots say m₁ and m₂ then m₁, m₂ are the slopes of tangents from P to the ellipse
∴ m₁m₂ = \(\left(\frac{y_{1}^{2}-b^{2}}{x_{1}^{2}-a^{2}}\right)\)
∴ -1 = \(\left(\frac{y_{1}^{2}-b^{2}}{x_{1}^{2}-a^{2}}\right)\)
[∵ The tangents are perpendicular to each
other so that m₁m₂ = -1]
i.e., x₁² + y₁² = a² + b²,
If, however, one of the perpendicular tangents is vertical, then such pair of perpendicular tangents intersect at one of the points (± a, ± b) and any of these points satisfies x² + y² = a² + b².
∴ The point of intersection of perpendicular tangents to the ellipse S = O lies on the circle x² + y² = a² + b².

Question 12.
Find the eccentricity, co-ordinates of foci, Length of latus reEtum and equations of directrices of the following ellipses.
i) 9x² + 16y² – 36x + 32y – 92 = 0
ii) 3x² + y² – 6x – 2y – 5 = 0 [T.S. Mar. 15]
Solution:
Given ellipse is :
9x² + 16y² – 36x + 32y – 92 = 0
9(x² -4x + 4) + 16 (y² + 2y + 1)
= 92 + 36 + 16
9 (x – 2)² + 16 (y + 1)2² = 144
comparing with \(\frac{(x-2)^{2}}{16}\) + \(\frac{(y+1)^{2}}{9}\) = 1,
we get
a² = 16, b² = 9 ⇒ a = 4, b = 3.
e = \(\sqrt{\frac{a^{2}-b^{2}}{a^{2}}}=\sqrt{\frac{16-9}{16}}=\frac{\sqrt{7}}{4}\)
Foci (h ± ae, k) = (2 ± 4 . \(\frac{\sqrt{7}}{4}\), -1)
= (2 ± \(\sqrt{7}\), -1)
Length of the latus rectum
= \(\frac{2 \cdot b^{2}}{a}=\frac{2.9}{4}=\frac{9}{2}\)
Equations of the directrices are x = h ± \(\frac{a}{e}\)
x = 2 ± \(\frac{4 \times 4}{\sqrt{7}}\)
\(\sqrt{7x}\) = 2\(\sqrt{7}\) ± 16

ii) 3x² + y² – 6x – 2y – 5 = 0
Solution:
3(x² – 2x) + (y² – 2y) = 5
⇒ 3(x² – 2x + 1) + (y² – 2y + 1) = 9
⇒ 3(x – 1)² + (y – 1)² = 9 .
comparing with ⇒ \(\frac{(x-1)^{2}}{3}\) + \(\frac{(y-1)^{2}}{9}\) = 1
we get
a < b ⇒ Y – axis is the major axis
a² = 3, b² = 9 .
a = \(\sqrt{3}\), b = 3, h = 1, k = 1
Length of major axis = 2b = 2(3) = 6
Length of minor axis = 2a = 2\(\sqrt{3}\)
Length of latus rectum = \(\frac{2 a^{2}}{b}=\frac{2.3}{3}\) = 2
Eccentricity = \(\sqrt{1-\frac{a^{2}}{b^{2}}}=\sqrt{1-\frac{3}{9}}=\sqrt{\frac{2}{3}}\)
Centre = (h, k) = (1, 1)
Focus = (h, k ± be) = (1, 1 ± 3 \(\left.\sqrt{\frac{2}{3}}\right)\))
= (1, 1 ± \(\sqrt{6}\))
Equation of directrices are y – k = ± \(\frac{b}{e}\)
y – 1 = ± \(\frac{3 \sqrt{3}}{\sqrt{2}}\)
y = 1 ± \(\frac{3 \sqrt{3}}{\sqrt{2}}\)

Question 13.
Find the equation of the ellipse referred to its major and minor axes as the co-ordinate axes x, y respectively with latus rectum of length 4 and the distance between foci 4\(\sqrt{2}\).
Solution:
Let the equation of the ellipse is \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
(a > b)
Length of the latus rectum = \(\frac{2 b^{2}}{a}\) = 4
⇒ b² = 2a.
Foci are S (ae, 0), S’ (-ae, 0)
Distance between the foci = 2ae = 4\(\sqrt{2}\)
ae = 2\(\sqrt{2}\)
b² = a² (1 – e²) = a² – (ae)²
2a = a² – 8 ⇒ a² – 2a – 8 = 0
(a – 4) (a + 2) = 0
a = 4 or – 2
a > 0 ⇒ a = 4
b² = 2a = 2 . 4 = 8
Equation of the ellipse is \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
\(\frac{x^{2}}{16}\) + \(\frac{y^{2}}{8}\) = 1
x² + 2y² = 16.

Question 14.
If the length of the latus rectum is equal to half of its minor axis of an ellipse in the standard form, then find the eccentricity of the ellipse.
Solution:
Let \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a> b) be the ellipse in its standard form.
Length of latus rectum = \(\frac{1}{2}\) (minor axis)
2 \(\frac{b^{2}}{a}\) = \(\frac{1}{2}\) (2b)
2 \(\frac{b^{2}}{a}\) = b
a = 2b
a² =4 b², ⇒ a² = 4a² (1 – e²)
∴ 1 – e² = \(\frac{1}{4}\) ⇒ e² = \(\frac{3}{4}\)
⇒ e = \(\frac{\sqrt{3}}{2}\).

Question 15.
If θ₁, θ₂ are the eccentric angles of the extremeties of a focal chord (other that the vertices) of the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a > b) and e Its eccentricity. Then show that
i) e cos \(\frac{\left(\theta_{1}+\theta_{2}\right)}{2}\) = cos \(\frac{\left(\theta_{1}-\theta_{2}\right)}{2}\)
ii) \(\frac{e+1}{e-1}\) = cot \(\left(\frac{\theta_{1}}{2}\right)\) . cot \(\left(\frac{\theta_{2}}{2}\right)\)
Solution:
Equation of the ellipse is \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1,
(a > b)

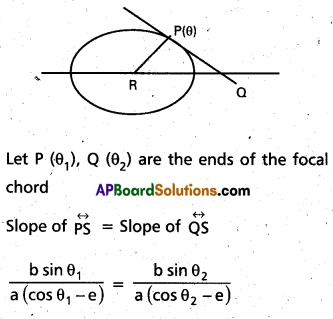
sin θ₁ . cos θ₂ – e sin θ₁ = cos θ₁ sin θ₂ – e . sin θ₂
sin θ₁ . cos θ₂ – cos θ₁ sin θ₂ = e sin θ₁ – e sin θ₂
sin (θ₁ – θ₂) = e (sin θ₁ – sin θ₂)
2 sin \(\frac{\left(\theta_{1}-\theta_{2}\right)}{2}\) . cos \(\frac{\left(\theta_{1}-\theta_{2}\right)}{2}\)
= e [2 cos \(\frac{\theta_{1}+\theta_{2}}{2}\) . sin \(\frac{\theta_{1}-\theta_{2}}{2}\)]

Question 16.
C is the centre1 AA’ and BB’ are major and minor axis of the ellipse.
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1. If PN is the ordinate of a point P on the ellipse then show that
\(\frac{(\mathrm{PN})^{2}}{\left(\mathrm{~A}^{\prime} \mathrm{N}\right)(\mathrm{AN})}\) = \(\frac{(\mathrm{BC})^{2}}{(\mathrm{CA})^{2}}\)
Solution:

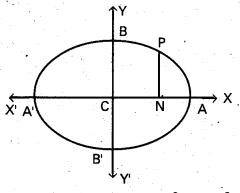
Equation of the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
P(a cos θ, b sin θ) any point on the ellipse.
PN = b sin θ; AN = a – a cos θ,
AN = a + a cos θ; BC = b, CA = a
(A’N). (AN) = (a + a cos θ) (a – a cos θ)
= a² – a²cos²θ
= a² (1 – cos θ)
= a² sin²θ
\(\frac{(\mathrm{PN})^{2}}{\left(\mathrm{~A}^{\prime} N\right)(\mathrm{AN})}=\frac{\mathrm{b}^{2} \sin ^{2} \theta}{\mathrm{a}^{2} \sin ^{2} \theta}=\frac{\mathrm{b}^{2}}{\mathrm{a}^{2}}\)
\(\frac{B C^{2}}{(C A)^{2}}=\frac{b^{2}}{a^{2}} \Rightarrow \frac{P^{2}}{\left(A^{1} N\right)(A N)}=\frac{(B C)^{2}}{(C A)^{2}}\)

Question 17.
S and Tare the foci of an ellipse and B is one end of the minor axis. If STB is an equilateral triangle, then find the eccentricity of the ellipse.
Solution:

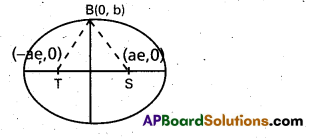
Let \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a > b) be an ellipse whose foci are S and T, B is an end of the minor axis such that STB is equilateral, then SB = ST = TB. We have S(ae, 0).
T = (-ae, 0) and B(0, b)
Consider SB = ST ⇒ (SB)² = (ST)²
⇒ (ae)² + b² = 4a²e²
∴ a²e² + a² (1 – e)² = 4a²e²
[∵ b² = a² (1 – e²)]
e² = \(\frac{1}{4}\)
∴ Eccentricity of the ellipse is \(\frac{1}{2}\).

Question 18.
Show that among the points on the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a > b), (-a, 0) is the farthest point and (a, 0) is the nearest point from the focus (ae, 0).
Solution:
Let P = (x, y) be any point on the ellipse so that – a ≤ x ≤ a and S = (ae, 0) be the focus.
Since (x, y) is on the ellipse,
y² = \(\frac{b^{2}}{a^{2}}\) (a² – x²)
= (1 – e²)(a² – x²) ………….. (1) [∵ b² = a²(1 – e²)]
Then we know that
sp² = (x – ae)² + y²
= (x – ae)² + (1 – e²)(a² – x²)
= -2xae + a² + e²x²
= [a – ex]²
∴ SP = [a – ex]
we have – a ≤ x ≤ a
⇒ -ae ≤ xe ≤ ae
⇒ -ae – a ≤ xe – a ≤ ae – a …………………. (2)
∴ ex – a < 0
∴ SP = a – ex …………………… (3)
From (2) and (3)
ae + a ≥ SP ≥ a – ae
⇒ a – ae ≤ SP ≤ ae + a
∴ Max SP = ae + a when P = (-a, 0)
and Min SP = a – ae when P = (a, 0)
Hence the nearest point is (a, 0) and the farthest one is (-a, 0).

Question 19.
The orbit of the Earth is an ellipse with eccentricity \(\frac{1}{60}\) with the Sun at one of its foci, the major axis being approximately 186 × 10⁶ miles in length. Find the shortest and longest distance of the Earth from the Sun.
Solution:
We take the orbit of the Earth to be
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a > b).
Since the major axis is 186 × 10⁶ miles,
2a = 186 × 10⁶ miles
∴ a = 93 × 10⁶ miles
If e be the eccentricity of the orbit, e = \(\frac{1}{60}\)
We know, the longest and shortest distances of the Earth from the Sun are respectively
a + ae and a – ae (problem 7)
Here, the longest distance
= 93 × 10⁶ × (1 + \(\frac{1}{60}\))
= 9455 × 10⁴ miles.
and the shortest distance
= 93 × 10⁶ × (1 – \(\frac{1}{60}\)) miles
= 9145 × 10⁴ miles.

Question 20.
Find the equation of the tangent and normal to the ellipse 9x² + 16y² = 144 at the end of the latus rectum in the first quadrant. A.P. [Mar. 15, Mar. 07]
Solution:
Given ellipse is 9x² + 16y² = 144

Equation of the normal at P is

Question 21.
If a tangent to the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a > b) meets its major.axis and minor axis atM and N respectively, then prove that \(\frac{a^{2}}{(C M)^{2}}\) + \(\frac{b^{2}}{(C N)^{2}}\) = 1. Where C is the centre of the ellipse.
Solution:
Let P(θ) (a cos θ, b sin θ) is any point on the ellipse then Equation of the tangent at P (θ) is

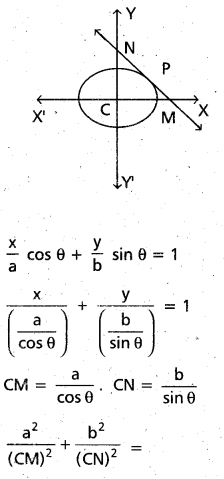
a² . \(\frac{\cos ^{2} \theta}{a^{2}}\) + b² . \(\frac{\sin ^{2} \theta}{b^{2}}\)
= cos² θ + sin² θ = 1.

Question 22.
Find the condition for the line
i) lx + my + n = 0 to be a tangent to the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
ii) lx+ my n = 0 to be a normal to the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1.
Solution:
i) Equation of the ellipse is \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1
Equation .of the tangent at P(θ) is
\(\frac{x}{a}\) cos θ + \(\frac{y}{b}\) sin θ = 1 ……………………… (1)
Equation of the given line is
lx + my = -n …………………. (2)
(1), (2) represent the same line. Comparing the co-efficients

Comparing (1) and (2)

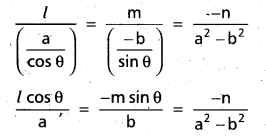
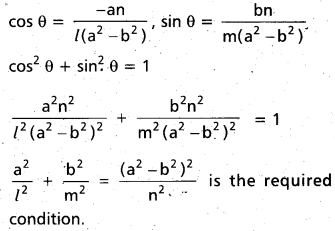
Question 23.
If the normal at one end of a latus rectum of the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 passes through one end of the minor axis, then show that e⁴ + e² = 1 [e is the eccentricity of the ellipse]
Solution:
Let L be the one end of the latus rectum of
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1. Then the coordinates of
L = (ae, \(\frac{b^{2}}{a}\))
Hence equation of the normal at L is

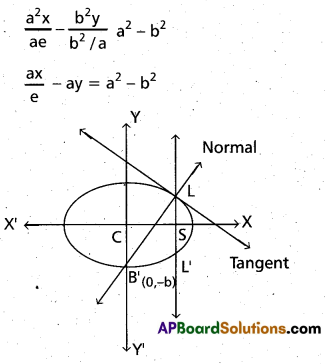
is a line passes through the one end
B’ = (0, -b)
or minor axis of \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 as shown in figure.
\(\frac{\mathrm{a}(0)}{\mathrm{e}}\) – a(-b) = a² – b²
ab = a2² – a² (1 – e²)
ab = a²e² ⇒ e² = \(\frac{b}{a}\) ⇒ e⁴ = \(\frac{b^{2}}{a^{2}}\)
= \(\frac{a^{2}\left(1-e^{2}\right)}{a^{2}}\) = 1 – e² ⇒ e⁴ + e² = 1.

Question 24.
If PN is the ordinate of a point P on the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 and the tangent at P meets the X – axis at T then show that (CN) (CT) = a² where C is the centre of the ellipse.
Solution:
Let P(θ) = (acosθ, bsinθ) be a point on the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1. Then the equation of the tangent at P(θ) is \(\frac{x \cos \theta}{a}\) + \(\frac{y \sin \theta}{b}\) = 1 or \(\frac{x}{\frac{a}{\cos \theta}}+\frac{y}{\frac{b}{\sin \theta}}=1\) meets the X – axis at T

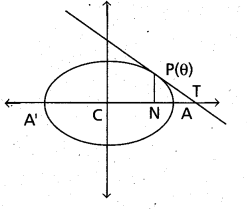
x – intercept (CT) = \(\frac{a}{\cos \theta}\) and the ordinate of P is PN = bsinθ
then its absicca CN = a cos θ. (see Fig.)
∴ (CN) . (CT) =, (a cos θ) (\(\frac{a}{\cos \theta}\)) = a².

Question 25.
Show that the points of intersection of the perpendicular tangets to an ellipse lie on a circle. [A.P. Mar. 16]
Solution:
Let the equation of the ellipse \(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 (a > b). Any tangent to it in the slope-intercept
form is y = mx ± \(\sqrt{a^{2} m^{2}+b^{2}}\) …………………. (1)
Let the perpendicular tangents intersed at
P(x₁, y₁).
∴ p lies on (1) for some real m, i.e.,
y₁ = mx₁ ± \(\sqrt{a^{2} m^{2}+b^{2}}\)
∴ (y₁ – mx₁)² = a²m² + b².
or
(x₁² – a²) m² – 2x₁y₁m + (y₁² – b²) = 0 being a quadratic equation in ‘m’, has two roots say m₁ and m₂ then m₁, m₂ are the slopes of tangents from P to the ellipse
∴ m₁m₂ = \(\left(\frac{y_{1}^{2}-b^{2}}{x_{1}^{2}-a^{2}}\right)\)
∴ – 1 = \(\left(\frac{y_{1}^{2}-b^{2}}{x_{1}^{2}-a^{2}}\right)\)
[∵ The tangents are perpendicular to each other so that m₁ m₂ = -1]
i.e., \(x_{1}^{2}\) + \(y_{1}^{2}\) = a² + b².
If, however, one of the perpendicular tangents is vertical, then such pair of perpendicular tangents intersect at one of the points (a, ± b) and any of these points satisfies x² + y² = a² + b².
∴ The point of intersection of perpendicular tangents to the ellipse S = 0 lies on the circle x² + y² = a²+ b².