Inter 2nd Year Maths 2B Integration Solutions Ex 6(b)

Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(b) will help students to clear their doubts quickly.

Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(b)

I. Evaluate the following integrals.

Question 1.
∫e^2x dx, x ∈ R.
Solution:
∫e^2x dx = \(\frac{e^{2x}}{2}\) + C

Question 2.
∫sin 7x dx, x ∈ R.
Solution:
∫sin 7x dx = \(\frac{\cos 7x}{7}\) + C

Question 3.
∫\(\frac{x}{1+x^2}\) dx, x ∈ R.
Solution:
∫\(\frac{xdx}{1+x^2}\) dx = \(\frac{1}{2}\)∫\(\frac{2xdx}{1+x^2}\) = \(\frac{1}{2}\) log(1+x²) + C

Question 4.
∫2xsin(x²+1) dx, x ∈ R.
Solution:
∫2x.sin(x²+1) dx, x ∈ R.
t = x² + 1 ⇒ dt = 2x dx
∫2x. sin(x²+1) dx = ∫ sin t dt = -cos t + C
= -cos (x²+1) + C

Question 5.
∫\(\frac{(logx)^2}{x}\) dx on I ⊂ (0, ∞).
Solution:
∫\(\frac{(logx)^2}{x}\) dx
t = log x ⇒ dt = \(\frac{1}{x}\) dx
∫\(\frac{(logx)^2}{x}\) dx = ∫t² dt
= \(\frac{(t^3}{3}\) + C = \(\frac{(logx)^3}{3}\) + C

Question 6.
dx on I ⊂ (1, ∞).
Solution:

Question 7.
∫\(\frac{\sin(Tan^{-1}x)}{1+x^2}\) dx, x ∈ R.
Solution:
∫\(\frac{\sin(tan^{-1}x)}{1+x^2}\) dx
t = tan^-1 x ⇒ dt = \(\frac{dx}{1+x^2}\)
∫\(\frac{\sin(tan^{-1}x)}{1+x^2}\)dx = ∫ sin t
= -cos t + t
= -cos (tan^-1 x) + C

Question 8.
∫\(\frac{1}{8+2x^2}\) dx on R.
Solution:

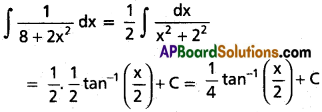
Question 9.
∫\(\frac{3x^2}{1+x^6}\)dx, on R.
Solution:

Question 10.
∫\(\frac{2}{\sqrt{25+9x^2}}\)dx on R.
Solution:

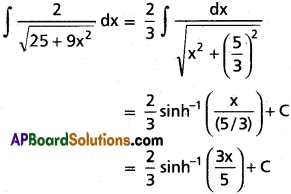
Question 11.
∫\(\frac{3}{\sqrt{9x^2-1}}\)dx on (\(\frac{1}{3}\), ∞).
Solution:

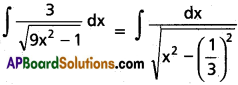
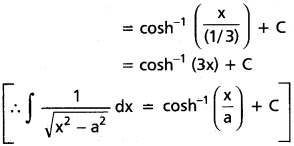
Question 12.
∫sin mx cos nx dx on R, m ≠ n, m and n are positive integers.
Solution:
∫sin mx cos nx = \(\frac{1}{2}\)∫ 2 sin mx. cos nx dx
= \(\frac{1}{2}\)∫sin(m+n)x + sin(m-n)x) dx
= –\(\frac{1}{2}\)(\(\frac{\cos (m+n) x}{m+n}+ cos\frac{(m-n)x}{m-n}\)) + C

Question 13.
∫sin mx sin nx dx on R, m ≠ n, m and n are positive integers.
Solution:
∫sin mx. sin nx dx = \(\frac{1}{2}\) ∫2 sin mx. sin nx dx
= \(\frac{1}{2}\)∫cos (m – n)x – cos (m + n)x dx
= \(\frac{1}{2}\)(\(\frac{\sin (m-n) x}{m-n}+\frac{\sin (m+n)x}{m+n}\)) + C

Question 14.
∫cos mx cos nx dx on R, m ≠ n, m and n are positive integers.
Solution:
∫cos mx. cos nx dx = \(\frac{1}{2}\) ∫2 cos mx.cos nx dx
= \(\frac{1}{2}\)∫cos (m + n)x – cos (m – n)x dx
= \(\frac{1}{2}\)(\(\frac{\sin (m+n) x}{m+n}+\frac{\sin (m-n)x}{m-n}\)) + C

Question 15.
∫sin x sin 2x. sin 3x dx on R.
Solution:
sin 2x . sin 3x = \(\frac{1}{2}\)(2 sin 3x. sin 2x)
= \(\frac{1}{2}\)(cos x – cos 5x)
sin x sin 2x sin 3x
= \(\frac{1}{2}\)(sin x . cos x – cos 5x . sin x)
= \(\frac{1}{2}\)(\(\frac{1}{2}\) sin 2x – \(\frac{1.2}{2}\)cos 5x . sin x)
= \(\frac{1}{2}\)(\(\frac{1}{2}\) sin 2x – \(\frac{1}{2}\) – (sin 6x – sin 4x)

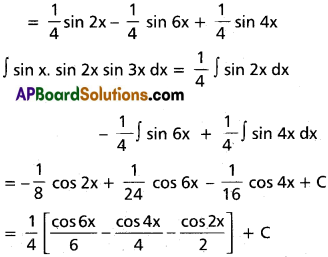
Question 16.
∫\(\frac{\sin x}{\sin(a+x)}\) dx on I ⊂ R\{nπ – a : n ∈ Z}.
Solution:
sin x = sin (a + x – a)
= sin (a + x) . cos a – cos (a + x) sin a
∫\(\frac{\sin x}{\sin(a+x)}\)dx
= cos a ∫ dx – sin a ∫\(\frac{\cos (a+x)}{\sin(a+x)}\) dx
= x . cos a – sin a . log |sin (a + x)| + c

II. Evaluate the following integrals.

Question 1.
∫(3x – 2)^½ dx on (\(\frac{2}{3}\), ∞)
Solution:
t = 3x – 2 ⇒ dt = 3 dx
∫(3x – 2)^½ dx = \(\frac{1}{3}\) ∫t^½ dt = \(\frac{1}{3}\) \(\frac{t^{3/2}}{3/2}\) + C
= \(\frac{2}{9}\)(3x – 2)^3/2 + C

Question 2.
∫\(\frac{1}{7x+3}\) dx on I ⊂ R\{-\(\frac{3}{7}\)}.
Solution:
∫\(\frac{1}{7x+3}\) dx
t = 7x + 3
⇒ dt = 7 dx
= ∫\(\frac{1}{7x+3}\) dx = \(\frac{1}{7}\) ∫\(\frac{dt}{t}\)
= \(\frac{1}{7}\) log |t| + C = \(\frac{1}{7}\) log|7x + 3| + C

Question 3.
∫\(\frac{log(1+x)}{1+x}\) dx on (-1, ∞).
Solution:
∫\(\frac{log(1+x)}{1+x}\) dx
t = 1 + x ⇒ dt = dx

Question 4.
∫(3x² – 4)x dx on R.
Solution:
∫(3x² – 4)x dx
t = 3x² – 4 ⇒ dt = 6x dx
∫(3x² – 4)x dx = \(\frac{1}{6}\)∫t dt = \(\frac{1}{6}\).\(\frac{t^2}{2}\) + C
= \(\frac{(3x^2-4)^2}{12}\) + C

Question 5.
∫\(\frac{dx}{\sqrt{1+5x}}\) dx on (-\(\frac{1}{5}\), ∞).
Solution:

Question 6.
∫(1 – 2x³)x² dx on R.
Solution:
∫(1 – 2x³)x² dx
t = 1 – 2x³ ⇒ dt = -6x² dx
∫(1 – 2x³)x² dx = –\(\frac{1}{6}\)∫t dt
= –\(\frac{1}{6}\) . \(\frac{t^2}{2}\) + C
= \(\frac{-(1-2x^3)^2}{12}\) + C

Question 7.
∫\(\frac{\sec^2 x}{(1+tan x)^3}\) dx on I ⊂ R \ {nπ – \(\frac{\pi}{4}\) : n ∈ Z}.
Solution:
∫\(\frac{\sec^2 x}{(1+tan x)^3}\) dx
t = 1 + tan x ⇒ dt = sec² x dx

Question 8.
∫x³ sinx⁴ dx on R.
Solution:
∫x³ . sinx⁴ dx
t = x⁴ ⇒ dt = 4x³ dx
∫x³ . sinx⁴ dx = \(\frac{1}{4}\)∫sin t. dt
= –\(\frac{1}{4}\)cos t + C
= –\(\frac{1}{4}\). cos x⁴ + C

Question 9.
∫\(\frac{\cos x}{(1+sin x)^2}\) dx on I ⊂ R\{2nπ + \(\frac{3 \pi}{2}\) : n ∈ Z}.
Solution:

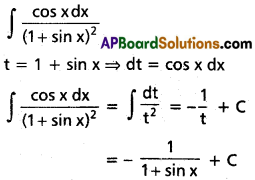
Question 10.
∫\(\sqrt[3]{sin x}\) cos x dx on [2nπ, (2n + 1)π], (n ∈ Z).
Solution:

Question 11.
∫ 2x e^x² dx on R.
Solution:
∫ 2x. e^x² dx
t = x² ⇒ dt = 2x dx
∫ 2xe^x² dt = ∫ e^t dt = e^t + C
= e^x² + C

Question 12.
∫\(\frac{e^{log x}}{x}\) dx on (0, ∞).
Solution:
∫\(\frac{e^{log x}}{x}\) dx
t = log x ⇒ dt = \(\frac{1}{x}\).dx
∫\(\frac{e^{log x}}{x}\) dx = ∫e^t. dt
= e^t + C
= e^{log x} + C
= x + C

Question 13.
∫\(\frac{x^2}{\sqrt{1-x^6}}\) dx on I = (-1, 1).
Solution:

Question 14.
∫\(\frac{2x^3}{1+x^8}\) dx on R.
Solution:
t = x⁴ ⇒ dt = 4x³ dx
∫\(\frac{2x^3}{1+x^8}\) = \(\frac{1}{2}\)∫\(\frac{dt}{1+t^2}\)
= \(\frac{1}{2}\) tan^-1 t + C
= \(\frac{1}{2}\) tan^-1(x⁴) + C

Question 15.
∫\(\frac{x^8}{1+x^18}\) dx on R.
Solution:
t = x⁹ ⇒ dt = 9x⁸ dx

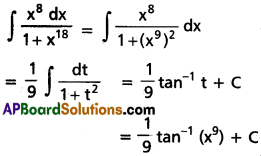
Question 16.
∫\(\frac{e^x(1+x)}{\cos^2(xe^x)}\) dx on I ⊂ R/{x ∈ R : cos (xe^x) = 0}.
Solution:
t = x . e^x
dt = (x . e^x + e^x)dx = e^x(1 + x)dx
∫\(\frac{e^x(1+x)}{\cos^2(xe^x)}\) dx = ∫\(\frac{dt}{\cos^2 t}\) dx
= ∫sin² t dt
= tan t + C
= tan (x. e^x) = C

Question 17.
∫\(\frac{cosec^2 x}{(a+b cot x)^5}\) dx on I ⊂ R\ {x ∈ R : a + b cot x = 0}, where a, b ∈ R, b ≠ 0.
Solution:
Let t = a + b cot x
dt = -b cosec² x dx
∫\(\frac{cosec^2 x}{(a+b cot x)^5}\) dx = –\(\frac{1}{b}\) ∫\(\frac{bt}{t^5}\)
= –\(\frac{1}{b}\) ∫t^-5 dt
= –\(\frac{1}{b}\) \(\frac{t^{-4}}{-4}\) + C
= \(\frac{1}{4b t^{4}}\) + C
= \(\frac{1}{4b(a+b cotx)^{4}}\) + C

Question 18.
∫e^x sin e^x dx on R.
Solution:
t = e^x ⇒ dt = e^x dx
∫e^x . sin e^x dx = ∫ sin t dt
= -cos t + C
= -cos (e^x) + C

Question 19.
∫\(\frac{\sin(log x)}{x}\) dx on (-1, ∞).
Solution:
t = log x ⇒ dt = \(\frac{1}{x}\) dx
∫\(\frac{\sin(log x)}{x}\)dx = ∫sin t dt
= -cos t + C
= -cos (log x) + C

Question 20.
∫\(\frac{1}{x log x}\) dx on (-1, ∞).
Solution:
t = log x
dt = \(\frac{1}{x}\) . dx
∫\(\frac{1}{x log x}\) dx = ∫\(\frac{1}{t}\)dt = log t + C = log(log x + C)

Question 21.
∫\(\frac{(1+log x)^n}{x}\) dx on (e^-1, ∞). n ≠ -1.
Solution:
t = 1 + log x
dt = \(\frac{1}{x}\) dx

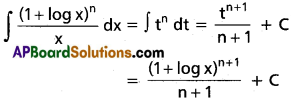
Question 22.
∫\(\frac{\cos(log x)}{x}\) dx on (0, ∞).
Solution:
t = log x
dt = \(\frac{1}{x}\) dx
∫\(\frac{\cos(log x)dx}{x}\) = ∫cos t dt
= sin t + C
= sin (log x) + C

Question 23.
∫\(\frac{\cos \sqrt{x}}{\sqrt{x}}\) dx on (0, ∞).
Solution:

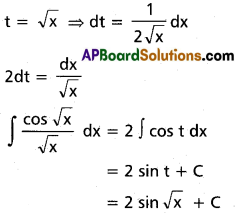
Question 24.
∫\(\frac{2x+1}{x^2+x+1}\) dx on R.
Solution:

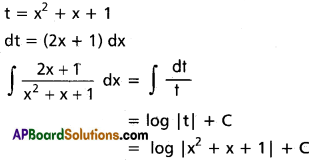
Question 25.
∫\(\frac{ax^{n-1}}{bx^n+c}\) dx, where n ∈ N, a, b, c are real nembers, b ≠ 0 and x ∈ I ⊂ {x ∈ R : xⁿ ≠ –\(\frac{c}{b}\)}.
Solution:
t = bxⁿ + C
dt = nbx^n-1dx

Question 26.
∫\(\frac{1}{x log x[log(log x)]}\) dx on (1, ∞).
Solution:

Question 27.
∫cot hx dx on R.
Solution:
t = sinh x ⇒ dt = cosh x dx
∫cot hx dx = ∫\(\frac{dt}{t}\)
= log |t| +C
= log |log(log x)| + C

Question 28.
∫\(\frac{1}{\sqrt{1-4x^2}}\) dx on (-\(\frac{1}{2}\), \(\frac{1}{2}\)).
Solution:

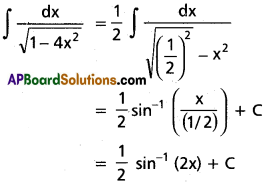
Question 29.
∫\(\frac{dx}{\sqrt{25+x^2}}\) dx on R.
Solution:

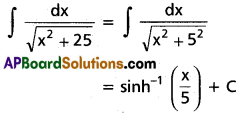
Question 30.
∫\(\frac{1}{(x+3\sqrt{x+2}}\) dx on I ⊂ (-2, ∞).
Solution:
x + 2 = t²
dx = 2t dt

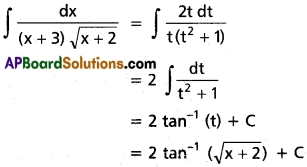
Question 31.
∫\(\frac{1}{1+\sin 2x}\) dx on I ⊂ R\{\(\frac{n \pi}{2}\) + (-1)ⁿ \(\frac{\pi}{4}\) : n ∈ Z}.
Solution:

Question 32.
∫\(\frac{x^2+1}{x^4+1}\) dx on R.
Solution:
∫\(\frac{x^2+1}{x^4+1}\) dx
Dividing Nr and Dr by x²

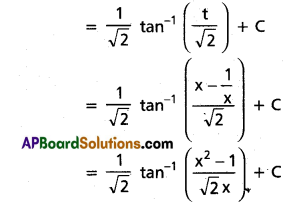
Question 33.
∫\(\frac{dx}{\cos^2+\sin 2x}\) on I ⊂ R\({(2n+1)\(\frac{\pi}{2}\) : n ∈ Z}∪{2nπ + tan^-1 \(\frac{1}{2}\) : n ∈ Z})
Solution:
∫\(\frac{dx}{\cos^2+\sin 2x}\)
Dividing Nr and Dr by cos² x

Question 34.
∫\(\sqrt{1-sin 2x}\) dx on I ⊂ {2nπ – \(\frac{3 \pi}{4}\), 2nπ + \(\frac{\pi}{4}\)}, n ∈ Z.
Solution:

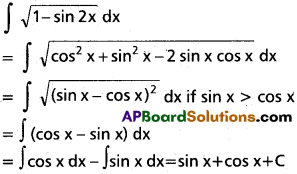
Question 35.
∫\(\sqrt{1+cos 2x}\) dx I ⊂ {2nπ – \(\frac{\pi}{2}\), 2nπ + \(\frac{\pi}{2}\)}, n ∈ Z.
Solution:
∫\(\sqrt{1+cos 2x}\) dx = ∫\(\sqrt{2cos^2 x}\) dx
= √2 ∫ cos x dx
= √2 sin x + C

Question 36.
∫\(\frac{\cos x + \sin x}{\sqrt{1+\sin 2x}}\) dx on I ⊂ {2nπ – \(\frac{\pi}{4}\), 2nπ + \(\frac{3\pi}{4}\)}, n ∈ Z.
Solution:

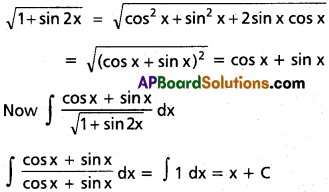
Question 37.
∫\(\frac{\sin 2x}{(a+b\cos x)^2}\) dx on {R, if |a| > |b| I ⊂ {x ∈ R : a + b cos x ≠ x}, if |a| < |b|.
Solution:
Put a + b cos x = t ⇒ cos x = \(\frac{t-a}{b}\)
Then b(-sin x)dx = dt
⇒ sin dx = \(\frac{-1}{b}\) dt

Question 38.
∫\(\frac{\sec x}{(\sec x+\tan x)^2}\) dx on I ⊂ R\{(2n + 1)\(\frac{\pi}{2}\) : n ∈ Z}.
Solution:
Put sec x + tan x = t
Then (sec x tan x + sec² x) dx = dt
sec x (sec x + tan x) dx = dt

Question 39.
∫\(\frac{dx}{a^2\sec^2 x+b^2\cos^2 x}\) on R, a ≠ 0, b ≠ 0.
Solution:

Question 40.
∫\(\frac{dx}{\sin(x-a)\sin(x-b)}\) on I ⊂ R\({a + nπ : n ∈ Z} ∪ {b + nπ n ∈ Z}).
Solution:

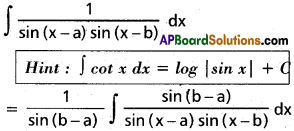
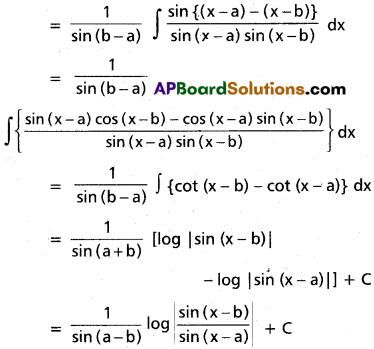
Question 41.
∫\(\frac{dx}{\sin(x-a)\sin(x-b)}\) on I ⊂ R\ ({a + \(\frac{(2n+1)\pi}{2}\) : n ∈ Z} ∪ {b + \(\frac{(2n+1)}{2}\)π : n ∈ Z}).
Solution:

III. Evaluate the following integers.

Question 1.
∫\(\frac{\sin 2x}{a \cos^2 x + b \sin^2 x}\) dx on I ⊂ R\ {x ∈ R |a cos² x + b sin² x = 0}.
Solution:
t = a cos² x + b sin² x
dt = (a(2cos x)(-sin x) + b(2sin x cos x))dx

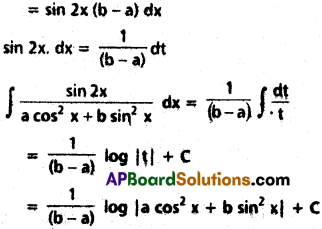
Question 2.
∫\(\frac{1-\tan x}{1+\tan x}\) dx for x ∈ I ⊂ R\ {nπ – \(\frac{\pi}{4}\) : n ∈ Z}.
Solution:

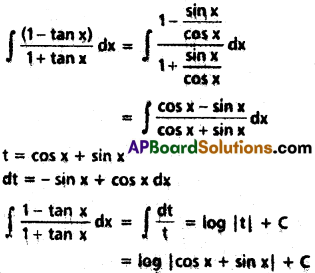
Question 3.
∫\(\frac{\cot(log x)}{x}\) dx, x ∈ I ⊂ (0, ∞)\{e^nπ : n ∈ Z}.
Solution:
t = log x ⇒ dt = \(\frac{dx}{x}\)
∫\(\frac{1-\tan x}{1+\tan x}\) dx = ∫cot t dt
= log(sin t) + C
= log |sin (log x)| + C

Question 4.
∫e^x . cot e^x dx, x ∈ I ⊂ R\ {log n π : n ∈ Z}.
Solution:
t = e^x ⇒ dt = e^x dx
∫e^x . cot e^x dx = ∫cot t dt
= log (sin t) + C
= log |sin(log x)| + C

Question 5.
∫sec (tan x) sec² x dx, on I ⊂ {x ∈ E : tan x ≠ \(\frac{(2k+1)\pi}{2}\) for any k ∈ Z}. where E = R / {\(\frac{(2n+1)\pi}{2}\) : n ∈ Z}.
Solution:
t = tan x ⇒ dt = sec² x dx
∫sec(tan x) sec² x dx = ∫sec t. dt
= log tan (\(\frac{\pi}{4}+\frac{t}{2}\) + C
= log (tan(\(\frac{\pi}{4}+\frac{\tan x}{2}\))) + C

Question 6.
∫\(\sqrt{sin x}\)cos dx on {2nπ, (2n + 1)π}, (n ∈ Z).
Solution:
t = sin x ⇒ dt = cos x dx
∫\(\sqrt{sin x}\)cos dx = ∫√t dt
= \(\frac{2}{3}\) = t^3/2 + C
= \(\frac{2}{3}\) = (sin x)^3/2 + C

Question 7.
∫tan⁴ x sec² x dx, x ∈ I ⊂ R\{\(\frac{(2n+1)\pi}{2}\) : n ∈ Z}.
Solution:
t = tan x ⇒ dt = sec² x dx
∫tan⁴ x sec² x dx = ∫t⁴dt
= \(\frac{t^5}{5}\) + C = \(\frac{(\tan x)^2}{5}\) + C

Question 8.
∫\(\frac{2x+3}{\sqrt{x^2+3x-4}}\) dx, x ∈ T ⊂ \{-4, 1}
Solution:
t = x² + 3x – 4
dt = (2x + 3)dx
∫\(\frac{2x+3}{\sqrt{x^2+3x-4}}\) = ∫\(\frac{dt}{\sqrt{t}}\)
= 2√t + C
= \(\sqrt{x^2+3x-4}\) + C

Question 9.
∫cosec² x\(\sqrt{\cot x}\) dx on (0, \(\frac{\pi}{2}\)).
Solution:
t = cot x ⇒ dt = -cosec² x dx
∫cosec² x\(\sqrt{\cot x}\) dx = -∫√t dt
= –\(\frac{2}{3}\) t√t + C
= –\(\frac{2}{3}\) cot(x)^3/2 + C

Question 10.
∫sec x log(sec x + tan x)dx on (0, \(\frac{\pi}{2}\)).
Solution:
t = log(sec x + tanx)
dt = \(\frac{(\sec x.\tan x+\sec^2 x)}{(\sec x +\tan x}\) = sec x dx
∫sec x .log(sec x + tan x)dx = ∫t dt
= \(\frac{t^2}{2}\) + C
= \(\frac{(log(\sec x+\tan x)^2}{2}\) + C

Question 11.
∫sin³ x dx on R.
Solution:
sin 3x = 3 sin x – 4 sin³ x
sin³ x = \(\frac{1}{4}\)(3 sin x – sin 3x)
∫sin³ x dx = \(\frac{3}{4}\)∫sin x – \(\frac{1}{4}\)∫sin 3x dx
= –\(\frac{3}{4}\) cos x + \(\frac{1}{12}\) cos 3x + C
= \(\frac{1}{12}\)(cos 3x – 9 cos x) + C

Question 12.
∫cos³ x dx on R.
Solution:
cos 3x = 4 cos³ x – 3 cos x
∫cos³ x dx = \(\frac{3}{4}\)∫cos x + \(\frac{1}{4}\)∫cos 3x dx
= –\(\frac{3}{4}\) sin x + \(\frac{1}{12}\) sin 3x + C
= \(\frac{1}{12}\)(9 sin x + 9 sin 3x) + C

Question 13.
∫cos x cos 2x dx on R.
Solution:
cos 2x cos x = \(\frac{1}{2}\)(2cos 2x cos x)
∫cos x cos 2x dx = \(\frac{1}{2}\)∫(cos 3x + cos x) dx
= \(\frac{1}{2}\)∫cos 3x + \(\frac{1}{2}\)∫cos x
= \(\frac{1}{2}\)(\(\frac{\sin 3x}{3}\) + sin x) + C
= \(\frac{\sin 3x+3\sin x}{6}\) + C

Question 14.
∫cos x cos 3x dx on R.
Solution:
cos 3x cos x = \(\frac{1}{2}\)(2cos 3x . cos x)
= \(\frac{1}{2}\)(cos 4x + cos 2x)
∫cos x cos 3x dx = \(\frac{1}{2}\)∫cos 4x dx + \(\frac{1}{2}\)∫cos 2x dx
= \(\frac{1}{2}\)(\(\frac{\sin 4x}{4}+\frac{\sin 2x}{2}\) + C
= \(\frac{1}{8}\)(sin 4x + 2sin 2x) + C

Question 15.
∫cos⁴ x dx on R.
Solution:
cos⁴ x = (cos² x)² = (\(\frac{1+\cos 2x}{2}\))²
= \(\frac{1}{4}\) (1 + 2 cos 2x+ cos² 2x)
= \(\frac{1}{4}\) (1 + 2 cos 2x + = \(\frac{1+\cos 4x}{2}\))
= \(\frac{1}{8}\) (2 + 4 cos 2x + 1 + cos 4x)
= \(\frac{1}{8}\) (3 + 4 cos 2x + cos 4x)
= \(\frac{1}{8}\)(3∫dx + 4∫cos 2x dx + ∫cos 4x dx)
= \(\frac{1}{8}\)(3x + 4\(\frac{\sin 2x}{2}+\frac{\sin 4x}{4}\)) + C
= \(\frac{1}{32}\)(12x + 8 sin 2x + sin 4x) + C

Question 16.
∫x \(\sqrt{4x+3}\) dx on (-\(\frac{3}{4}\), ∞).
Solution:

Question 17.
∫\(\frac{dx}{\sqrt{a^2-(b+cx)^2}}\) on {x ∈ R : |b + cx| < a}. where a, b, c are real numbers c ≠ 0 and a > 0.
Solution:

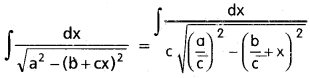
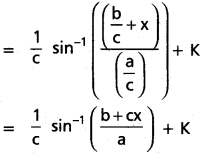
Question 18.
∫\(\frac{dx}{a^2+(b+cx)^2}\) on R, a, b, c are real numbers, c ≠ 0 and a > 0.
Solution:

Question 19.
∫\(\frac{dx}{1+e^x}\), x ∈ R
Solution:

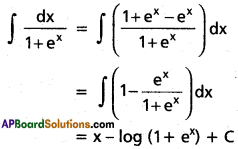
Question 20.
∫\(\frac{x^2}{(a+bx)^x}\) dx, x ∈ I ⊂ R\{-\(\frac{a}{b}\)}, where a, b are real nembers, b ≠ 0.
Solution:
Put t = a + bx
dt = b dx ⇒ dx = \(\frac{1}{b}\). dt

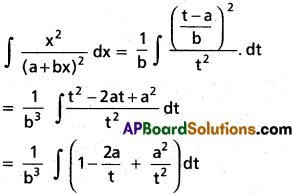
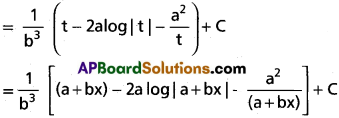
Question 21.
∫\(\frac{x^2}{\sqrt{1-x}}\) dx, x ∈ (-∞, 1).
Solution: