Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Integration Solutions Exercise 6(e) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Integration Solutions Exercise 6(e)
I. Evaluate the following integrals.
Question 1.
∫\(\frac{x-1}{(x-2)(x-3)}\)dx
Solution:
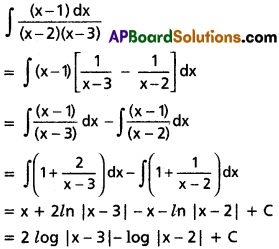
Question 2.
∫\(\frac{x^2}{(x+1)(x+2)^2}\)dx
Solution:
∫\(\frac{x^2}{(x+1)(x+2)^2}\) ≡ \(\frac{A}{x+1}+\frac{B}{x+2}+\frac{C}{(x+2)^2}\)
⇒ x² = A(x + 2)² + B(x + 1)(x + 2) + (x + 1) …………….. (1)
Put x = -2 in (1)
(-2)² = A(0) + B(0) + C(-2 + 1) ⇒ C = -4
Put x = -1 in (1)
(-1)² = A(-1 + 2)² + B(0) + C(0)
⇒ A = 1
Equation coeffs. of x² in (1)
1 = A + B
⇒ B = 1 – A = 1 – 1 = 0
∴ \(\frac{x^2}{(x+1)(x+2)^2}=\frac{1}{x+1}+\frac{0}{x+2}+\frac{(-4)}{(x+2)^2}\)
∴ ∫\(\frac{x^2}{(x+1)(x+2)^2}\)dx
= ∫\(\frac{1}{x+1}\)dx – 4∫\(\frac{1}{(x+2)^2}\)dx
= log|x + 1| – 4\(\frac{(-1)}{x+2}\)
= log|x + 1| + \(\frac{4}{x+2}\) + C
![]()
Question 3.
∫\(\frac{x+3}{(x-1)(x^2+1)}\)dx
Solution:
Let \(\frac{x+3}{(x-1)(x^2+1)}=\frac{A}{x-1}+\frac{Bx+C}{x^2+1}\)
⇒ (x + 3) = A(x² + 1) + (Bx + C)(x – 1) …………….. (1)
Put x = 0 in (1)
3 = A(1) + C(-1)
⇒ A – C = 3 ⇒ C = A – 3 = 2 – 3 = -1
Equation coefficient of x² in (1)
0 = A + B
⇒ B = -A = -2
∴ \(\frac{x+3}{(x-1)(x^2+1)}=\frac{+2}{(x-1)}+\frac{-2x-1}{x^2+1}\)
∫\(\frac{x+3}{(x-1)(x^2+1)}\)dx = 2∫\(\frac{1}{x-1}\)dx
-∫\(\frac{2x}{x^2+1}\)dx – ∫\(\frac{1}{x^2+1}\)dx
= 2 log |x – 1| – log |x² + 1| – tan-1(x) + C
Question 4.
![]()
Solution:

Question 5.
∫\(\frac{dx}{(e^x+e^{2x}}\)
Solution:
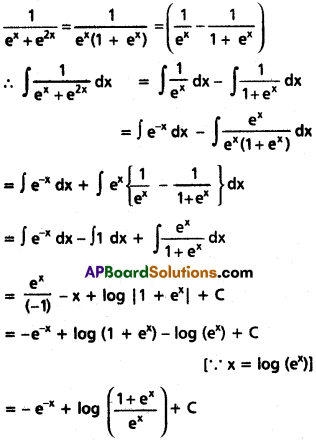
![]()
Question 6.
∫\(\frac{dx}{(x+1)(x+2)}\)
Solution:
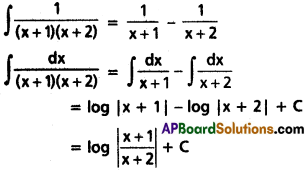
Question 7.
∫\(\frac{1}{(e^x-1}\)dx
Solution:
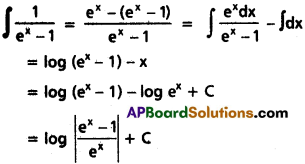
Question 8.
∫\(\frac{1}{(1-x)(4+x^2)}\)dx
Solution:
Let \(\frac{1}{(1-x)(4+x^2)}=\frac{A}{1-x}+\frac{Bx+C}{4+x^2}\)
⇒ 1 = A(4 + x²) + (Bx + C)(1 – x) ………….. (1)
Put x = 1 in (1)
1 = A(4 + 1) ⇒ A = \(\frac{1}{5}\)
Put x = 0 in (1)
1 = A(4) + C(1)
⇒ C = 1 – 4A = 1 – 4(\(\frac{1}{5}\)) = \(\frac{5-4}{5}\) = \(\frac{1}{5}\)
0 = A – B
⇒ B = A = \(\frac{1}{5}\)

![]()
Question 9.
∫\(\frac{2x+3}{x^3+x^2-2x}\)dx
Solution:
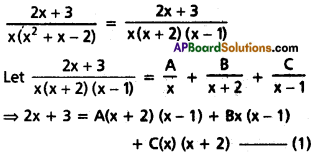
Put x = 0 in (1), then
3 = A(2)(-1) + B(0) + C(0)
⇒ A = –\(\frac{3}{2}\)
Put x = 1 in (1). Then
2 + 3 = A(0) + B(0) + C(1)(3)
⇒ C = \(\frac{5}{3}\)
Put x = -2 in (1). Then
2(-2) + 3 = A(0) + B(-2)(-2 – 1) + C(0)
⇒ -1 = 6B ⇒ B = \(\frac{-1}{6}\)

II. Evaluate the following integrals.
Question 1.
∫\(\frac{dx}{6x^2-5x+1}\)
Solution:


Question 2.
∫\(\frac{dx}{x(x+1)(x+2)}\)
Solution:
\(\frac{1}{x(x+1)(x+2)}\) ≡ \(\frac{A}{x}+\frac{B}{x+1}+\frac{C}{x+2}\)
⇒ 1 ≡ A(x + 1)(x + 2) + B(x)(x + 2) + C(x)(x + 1)
Put x = 0
1 = A(1)(2) + B(0) + C(0) ⇒ A = \(\frac{1}{2}\)
Put x = -1
1 = A(0) + B(0) + C(-2)(-2 + 1)
⇒ C = \(\frac{1}{2}\)
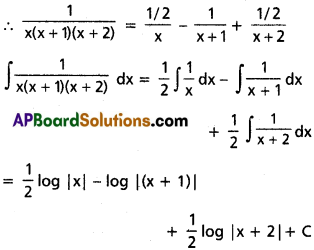
![]()
Question 3.
∫\(\frac{3x-2}{(x-1)(x+2)(x-3)}\)dx
Solution:
\(\frac{3x-2}{(x-1)(x+2)(x-3)}\) ≡ \(\frac{A}{x-1}+\frac{B}{x+2}+\frac{C}{x-3}\)
⇒ 3x – 2 = A(x + 2)(x – 3) + B(x – 1)(x – 3) + C(x – 1)(x + 2)
Put x = 1
3(1) – 2 = A(1 + 2)(1 – 3) + B(0) + C(0)
⇒ A = \(\frac{-1}{6}\)
Put x = 3
3(3) – 2 = A(0) + B(0) + C(3 – 1)(3 + 2)
C = \(\frac{7}{10}\)
Put x = -2
3(-2) – 2 = A(0) + B(-2 – 1)(-2 – 3) + C(0) – 8
= 15B ⇒ B = \(\frac{-8}{15}\)

Question 4.
∫\(\frac{7x-4}{(x-1)^2(x+2)}\)dx
Solution:
\(\frac{7x-4}{(x-1)^2(x+2)}\) ≡ \(\frac{A}{x-1}+\frac{B}{(x-1)^2}+\frac{C}{x+2}\)
⇒ 7x – 4 = A(x – 1)(x + 2) + B(x + 2) + C(x – 1)² ………….. (1)
Put x = 1 in (1)
7 – 4 = A(0) + B(1 + 2) ⇒ B = 1
Put x = -2 in (1)
7(-2) – 4 = A(0) + B(0) + C(-2 – 1)²
⇒ -18 = 9C ⇒ C = -2
Equating coeffs. of x² in (1)
0 = A + C ⇒ A = -C = 2
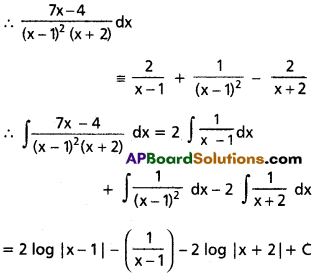
III. Evaluate the following integrals.
Question 1.
∫\(\frac{1}{(x-a)(x-b)(x-c)}\)dx
Solution:


Question 2.
∫\(\frac{2x+3}{(x+3)(x^2+4)}\)dx
Solution:
\(\frac{2x+3}{(x+3)(x^2+4)}\) = \(\frac{A}{x+3}+\frac{Bx+C}{x^2+4}\)
2x + 3 = A(x² + 4) + (Bx + C)(x + 3)
x = -3 ⇒ -3 = A(9 + 4) = 13A
A = –\(\frac{3}{13}\)
Equating the coefficient of x²
0 = A + B ⇒ B = -A = \(\frac{3}{13}\)
Equating the constants
3 = 4A + 3C

![]()
Question 3.
∫\(\frac{2x^2+x+1}{(x+3)(x-2)^2}\)dx
Solution:
Let \(\frac{2x^2+x+1}{(x+3)(x-2)^2}\) = \(\frac{A}{x+3}+\frac{B}{x-2}+\frac{C}{(x-2)^2}\)
2x² + x + 1 = A(x – 2)² + B(x + 3)(x – 2) + C(x + 3)
x = 2 ⇒ 8 + 2 + 1 = C(2 + 3) = 5C
⇒ C = \(\frac{11}{5}\)
x = -3 ⇒ 18 – 3 + 1
= A(-5)² = 25 A ⇒ A = \(\frac{16}{25}\)
Equating the coefficients of x²
2 = A + B ⇒ B = 2 – A = 2 – \(\frac{16}{25}\) = \(\frac{34}{25}\)
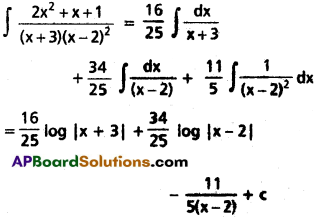
Question 4.
∫\(\frac{dx}{x^3+1}\)dx
Solution:
\(\frac{1}{x^3+1}\) = \(\frac{1}{(x+1)(x^2-x+1)}\)
Let \(\frac{1}{x^3+1}\) = \(\frac{1}{x+1}+\frac{1}{x^2-x+1}\)
⇒ 1 = A(x² – x + 1) + (Bx + C)(x + 1) ……………. (1)
Put x = -1 in (1)
1 = A(1 + 1 + 1) + (-B + C)(0)
⇒ 3A = 1 ⇒ A = \(\frac{1}{3}\)
Put x = 0 in (1)
1 = A(1) + C(1)
⇒ C = 1 – A = 1 – \(\frac{1}{3}=\frac{2}{3}\)
Equating the coefficients of x²
O = A + B ⇒ B = -A = –\(\frac{1}{3}\)

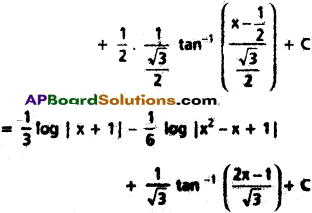
![]()
Question 5.
∫\(\frac{\sin x \cos x}{\cos^2 x+3cos x+2}\)dx
Solution:
Put cos x = t ⇒ – sin x dx = dt
∫\(\frac{\sin x \cos x}{\cos^2 x+3cos x+2}\)dx = ∫\(\frac{-t dt}{t^2+3t+2}\)
= -∫\(\frac{t}{t^2+3t+2}\)dt …………. (1)
Let \(\frac{t}{t^2+3t+2}\) = \(\frac{t}{(t+1)(t+2)}\)
= \(\frac{A}{t+1}+\frac{B}{t+2}\)
⇒ t = A(t + 2) + B(t + 1) ………… (2)
Put t = -1 in (2)
-1 = A(-1 + 2) ⇒ A = -1
Put t = -2 in (2)
-2 = B(-2 + 1) ⇒ B = 2
∴ \(\frac{t}{t^2+3t+2}\) = \(\frac{-1}{t+1}+\frac{2}{t+2}\) ……….. (3)
∴ From (1) & (2)
∫\(\frac{\sin x.\cos x}{\cos^2 x+3cos x+2}\)dx
= -[∫\(\frac{-1}{t+1}\)dt+2∫\(\frac{1}{t+2}\)]
= ∫\(\frac{1}{t+1}\) – 2∫\(\frac{1}{t+2}\)
= log|t + 1| – 2log|t + 2| + C
= log|1 + cos x| – 2log|2 + cos x| + C
= log|1 + cos x| – log(2 + cos x)² + C
= log|\(\frac{1+\cos x}{(2+\cos x)^2}\)| + C