Use these Inter 2nd Year Maths 2B Formulas PDF Chapter 3 Parabola to solve questions creatively.
Intermediate 2nd Year Maths 2B Parabola Formulas
Definition:
→ Conic section: If right circular solid cone is cut by a plane the section of it is called a Conic section.
→ Conic: The locus of a point whose distances from a fixed point and a fixed straight line are in constant ratio ‘e’ is called a conic.
→ Parabola : A conic with eccentricity 7 is called a parabola i.e., the locus of a point, whose distance from fixed point (focus) is equal to the distance from a fixed straight line (directrix) is called a parabola.
→ Axis of Parabola: The line passing through the vertex and the focus and perpendicular to directrix of the parabola is called the axis of the Parabola.
→ Equation of Parabola : General form – Let S(α, β) be the focus and ax + by + c = 0 be directrix then by definition the equation of parabola be,
\(\sqrt{(x-\alpha)^{2}+(y-\beta)^{2}}\) = \(\left|\frac{a x+b y+c}{\sqrt{a^{2}+b^{2}}}\right|\)
![]()
Various forms of parabola:
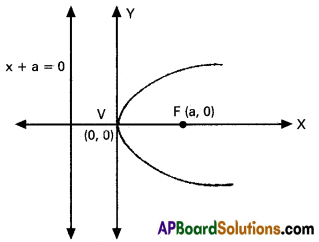
→ y2 = 4ax
Axis : X – axis
Focus : (a, 0)
Vertex : (0, 0)
Equation of directrix : x + a = 0
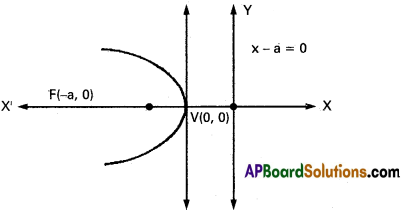
→ y2= – 4ax
Axis: x – axis
Focus: (- a, 0)
Vertex : (0, 0)
Equation of directrix : x – a = 0
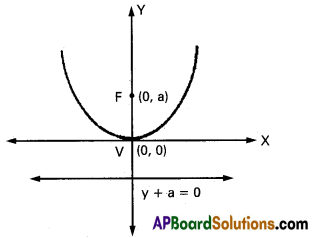
→ x2 = 4ay (a > 0)
Axis: Y-axis Focus : (0, a)
Vertex : (0, 0)
Equation of directrix: y + a = 0
![]()
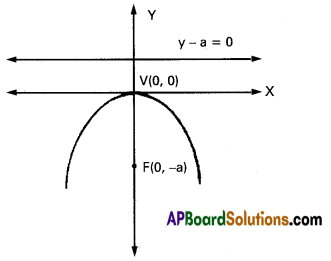
→ x2 = -4ay(a>0)
Axis : Y axis
Focus : (0, – a)
Vertex: (0, 0)
Equation of directrix : y – a = 0
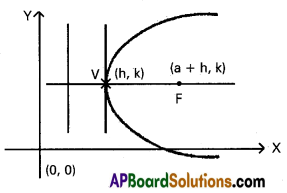
→ (y – k)2 = 4a (x – h) a > 0
Axis : y = k’ a line parallel to X- axis
Focus : (a + h, k)
Vertex: (h, k)
Equation of directrix: x + a = h
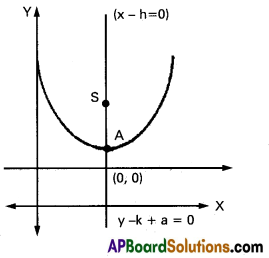
→ (x – h)2 = 4a (y – k) a > 0
Axis: x = h a line parallel to Y-axis
Focus: (h, a + k)
Vertex: (h, k)
Equation of directrix: y + a = k
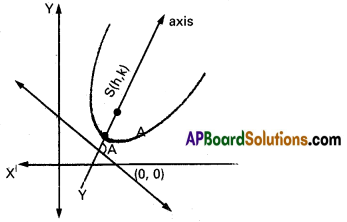
→ \(\sqrt{(x-h)^{2}+(y-k)^{2}}\) = \(\left|\frac{a x+b y+c}{\sqrt{a^{2}+b^{2}}}\right|\)
Axis: b(x – h) – a(y – k) = 0
Focus: (h, k)
Vertex: Some point A(fig)
Equation of directrix : ax + by + c = 0
Chord: Line segment joining two points of a parabola is called a, chord of the parabola. If this chord passes through focus is called focal chord.
Chord passing through focus and ⊥ to axis is called latus rectum.
Length of latus rectum = 4a
![]()
Parametric form of parabola:
For y2 = 4ax
Parametric form will be x = at2, y = 2at
Definition:
→ The locus of a point which moves in a plane so that its distance from a fixed point bears a constant ratio to its distance from a fixed straight line is called a conic section or conic. The fixed point is called focus, the fixed straight line is called directrix and the constant ratio ‘e’ is called eccentricity of the conic.
If e = 1, then the conic is called a Parabola.
If e < 1, then the conic is called an Ellipse. If e > 1, then the conic is called a hyperbola.
Note: The equation of a conic is of the form ax2 + 2hxy + by2 + 2gx + 2fy + c = 0.
→ Directrix of the Conic: A line L = 0 passing through the focus of a conic is said to be the principal axis of the conic if it is perpendicular to the directrix of the conic.
→ Vertices: The points of intersection of a conic and its principal axis are called vertices of the conic.
→ Centre: The midpoint o the line segment joining the vertices of a conic is called centre of the conic.
→ Note 1: If a conic has only one vertex then its centre coincides with the vertex.
→ Note 2: If a conic has two vertices then its centre does not coincide either of the vertices. In this case the conic is called a central conic.
→ Standard Form: A conic is said to be in the standard form if the principal axis of the conic is x-axis and the centre of the conic is the origin.
Equation of a Parabola in Standard Form:
The equation of a parabola in the standard form is y2 = 4ax.
Proof :
Let S be the focus and L = 0 be the directrix of the parabola.
Let P be a point on the parabola.
Let M, Z be the projections of P, S on the directrix L = 0 respectively.
Let N be the projection of P on SZ.
Let A be the midpoint of SZ.
Therefore, SA = AZ, ⇒ A lies on the parabola. Let AS = a.
Let AS, the principal axis of the parabola as x-axis and Ay perpendicular to SZ as y-axis.
Then S = (a, 0) and the parabola is in the standard form.
Let P = (x1, y1).
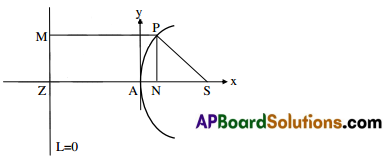
Now PM = NZ = NA + AZ = x1 + a
P lies on the parabola ⇒ \(\frac{\mathrm{PS}}{\mathrm{PM}}\) = 1 ⇒ PS = PM
⇒ \(\sqrt{\left(x_{1}-a\right)^{2}+\left(y_{1}-0\right)^{2}}\) = x1 + a
⇒ (x1 – a)2 + y12 = (x1 + a)2
⇒ y12 = (x1 + a)2 – (x1 – a)2
⇒ y12 = 4ax1
The locus of P is y2 = 4ax.
∴ The equation to the parabola is y2 = 4ax.
![]()
Nature of the Curve y2 = 4ax.
(i) The curve is symmetric with respect to the x-axis.
∴ The principal axis (x-axis) is an axis of the parabola.
(ii) y = 0 ⇒ x = 0. Thus the curve meets x-axis at only one point (0, 0).
Hence the parabola has only one vertex.
(iii) If x < 0 then there exists no y ∈ R. Thus the parabola does not lie in the second and third quadrants. (iv) If x > 0 then y2 > 0 and hence y has two real values (positive and negative). Thus the parabola lies in the first and fourth quadrants.
(v) x = 0 ⇒ y2 = 0 ⇒ y = 0, 0. Thus y-axis meets the parabola in two coincident points and hence y-axis touches the parabola at (0, 0).
(vi) As x → ∞ ⇒ y2 → ∞ ⇒ y → ±∞
Thus the curve is not bounded (closed) on the right side of the y-axis.
→ Double Ordinate: A chord passing through a point P on the parabola and perpendicular to the principal axis of the parabola is called the double ordinate of the point P.
→ Focal Chord: A chord of the parabola passing through the focus is called a focal chord.
→ Latus Rectum: A focal chord of a parabola perpendicular to the principal axis of the parabola is called latus rectum. If the latus rectum meets the parabola in L and L’, then LL’ is called length of the latus rectum.
Theorem: The length of the latus rectum of the parabola y2 = 4ax is 4a.
Proof:
Let LL’ be the length of the latus rectum of the parabola y2 = 4ax.
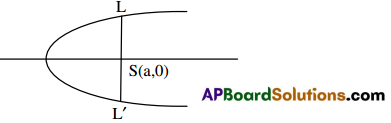
Let SL = 1, then L = (a, 1)
Since L is a point on the parabola y2 = 4ax, therefore 12 = 4a(a)
⇒ 12 = 4a2 ⇒ 1 = 2a ⇒ SL = 2a
∴ LL’ = 2SL = 4a.
![]()
→ Focal Distance: If P is a point on the parabola with focus S, then SP is called focal distance of P.
Theorem: The focal distance of P(x1, y1) on the parabola y2 = 4ax is x1 + a.
Notation: We use the following notation in this chapter
S ≡ y2 – 4ax
S1 ≡ YY1 – 2a(x + x1)
S11 = S(x1, y1) ≡ y12 – 4ax1
S12 ≡ y1y2 – 2a(x1 + x2)
Note:
Let P(x1, y1) be a point and S ≡ y2 – 4ax = 0 be a parabola. Then
- P lies on the parabola ⇔ S11 = 0
- P lies inside the parabola ⇔ S11 = 0
- P lies outside the parabola ⇔ S11 = 0
Theorem: The equation of the chord joining the two points A(x1, y1), B(x2, y2) on the parabola S = 0 is S1 + S2 = S12.
Theorem: The equation of the tangent to the parabola S = 0 at P(x1, y1) is S1 = 0.
Normal:
Let S = 0 be a parabola and P be a point on the parabola S = 0. The line passing through P and perpendicular to the tangent of S = 0 at P is called the normal to the parabola S = 0 at P.
Theorem: The equation of the normal to the parabola y2 = 4ax at P(x1, y1) is y1(x – x1) + 2a(y – y1) = 0.
Proof:
The equation of the tangent to S = 0 at P is S1 = 0

⇒ yy1 – 2a(x + x1) = 0.
⇒ yy1 – 2ax – 2ax1 = 0
The equation of the normal to S = 0 at P is:
y1(x – x1) + 2a(y – y1) = 0
![]()
Theorem: The condition that the line y = mx + c may be a tangent to the parabola y2 = 4ax is c = a/m.
Proof:
Equation of the parabola is y2 = 4ax ……….. (1)
Equation of the line is y = mx + c ………. (2)
Solving (1) and (2),
(mx + c)2 = 4ax ⇒ m2x2 + c2 + 2mcx = 4ax
⇒ m2x2 + 2(mc – 2a)x + c2 = 0
Which is a quadratic equation in x. Therefore it has two roots.
If (2) is a tangent to the parabola, then the roots of the above equation are equal.
⇒ its disc eminent is zero
⇒ 4(mc – 2a)2 – 4m2c2 = 0
⇒ m2c2 + 4a2 – 4amc – m2c2 = 0
⇒ a2 – amc = 0
⇒ a = mc
⇒ C = \(\frac{a}{m}\)
II Method:
Given parabola is y2 = 4ax.
Equation of the tangent is y = mx + c ———— (1)
Let P(x1, y1) be the point of contact.
The equation of the tangent at P is
yy1 – 2a(x + x1) = 0 ⇒ yy1 = 2ax + 2ax1 ……. (2)
Now (1) and (2) represent the same line.
∴ \(\frac{\mathrm{y}_{1}}{1}=\frac{2 \mathrm{a}}{\mathrm{m}}=\frac{2 \mathrm{ax}_{1}}{\mathrm{c}}\) ⇒ x1 = \(\frac{\mathrm{c}}{\mathrm{m}}\), y1 = \(\frac{\mathrm{2a}}{\mathrm{m}}\)
P lies on the line y = mx + c ⇒ y1 = mx1 + c
⇒ \(\frac{2 \mathrm{a}}{\mathrm{m}}=\mathrm{m}\left(\frac{\mathrm{c}}{\mathrm{m}}\right)+\mathrm{c} \Rightarrow \frac{2 \mathrm{a}}{\mathrm{m}}=2 \mathrm{c} \Rightarrow \mathrm{c}=\frac{\mathrm{a}}{\mathrm{m}}\)
Note: The equation of a tangent to the parabola y2 = 4ax can be taken as y = mx + a/m. And the point of contact is (a/m2, 2a/m).
![]()
Corollary: The condition that the line lx + my + n = 0 to touch the parabola y2 = 4ax is am2 = ln.
Proof:
Equation of the parabola is y2 = 4ax …………. (1)
Equation of the line is lx + my + n = 0
⇒ y = – \(\frac{1}{\mathrm{~m}}\)x – \(\frac{\mathrm{n}}{\mathrm{m}}\)
But this line is a tangent to the parabola, therefore
C = a/m ⇒ \(-\frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{a}}{-1 / \mathrm{m}} \Rightarrow \frac{\mathrm{n}}{\mathrm{m}}=\frac{\mathrm{am}}{1}\) ⇒ am2 = ln
Hence the condition that the line lx + my + n = 0 to touché the parabola y2 = 4ax is am2 = ln.
Note: The point of contact of lx + my + n = 0 with y2 = 4ax is (n/l, – 2am/l).
Theorem: The condition that the line lx + my + n = 0 to touch the parabola x2 = 4ax is al2 = mn.
Proof:
Given line is lx + my + n = 0 …… (1)
Let P(x1, y1) be the point of contact of (1) with the parabola x2 = 4ay.
The equation of the tangent at P to the parabola is xx1 = 2a(y + y1)
⇒ x1x – 2ay – 2ay1 = 0 …… (2)
Now (1) and (2) represent the same line.
∴ \(\frac{\mathrm{x}_{1}}{1}=-\frac{2 \mathrm{a}}{\mathrm{m}}=-\frac{2 \mathrm{ay}_{1}}{\mathrm{n}}\) ⇒ x1 = – \(-\frac{2 \mathrm{al}}{\mathrm{m}}\), y1 = \(\frac{n}{m}\)
P lies on the line lx + my + n = 0
⇒ lx1 + my1 + n = 0 ⇒ l\(\left(\frac{-2 a l}{m}\right)\) + m\(\left(\frac{\mathrm{n}}{\mathrm{m}}\right)\) + n = 0
⇒ – 2al2 + mn + mn = 0 ⇒ al2 = mn
Theorem: Two tangents can be drawn to a parabola from an external point.
Note:
1. If m1, m2 are the slopes of the tangents through P, then m1, m2 become the roots of
equation (1). Hence m1 + m2 = y1/x1, m1m2 = a/x1.
2. If P is a point on the parabola S =0 then the roots of equation (1) coincide and hence only one tangent can be drawn to the parabola through P.
3. If P is an internal point to the parabola S = 0 then the roots of (1) are imaginary and hence no tangent can be drawn to the parabola through P.
Theorem: The equation in the chord of contact of P(x1, y1) with respect to the parabola S = 0 is S1 = 0.
Theorem: The equation of the chord of the parabola S = 0 having P(x1, y1) as its midpoint is S1 = S11.
![]()
Pair of Tangents:
Theorem: The equation to the pair of tangents to the parabola S = 0 from P(x1, y1) is S12 = s11s.
Parametric Equations of the Parabola:
A point (x, y) on the parabola y2 = 4ax can be represented as x = at2, y = 2at in a single parameter t. Theses equations are called parametric equations of the parabola y2 = 4ax. The point (at2, 2at) is simply denoted by t.
Theorem: The equation of the tangent at (at2, 2at) to the parabola is y2 = 4ax is yt = x + at2.
Proof:
Equation of the parabola is y2 = 4ax.
Equation of the tangent at (at2, 2at) is S1 = 0.
⇒ (2at)y – 2a(x + at2) = 0
⇒ 2aty = 2a(x + at2) ⇒ yt = x + at2.
Theorem: The equation of the normal to the parabola y2 = 4ax at the point t is y + xt = 2at + at3.
Proof:
Equation of the parabola is y2 = 4ax.
The equation of the tangent at t is:
yt = x + at2 = x – yt + at2 = 0
The equation of the normal at (at2, 2at) is
t(x – at2) + l(y – 2at) = 0
⇒ xt – at3 + y – 2at = 0 ⇒ y + xt = 2at + at3
Theorem: The equation of the chord joining the points t1 and t2 on the parabola y2 = 4ax is y(t1 + t2) = 2x + 2at1t2.
Proof:
Equation of the parabola is y2 = 4ax.
Given points on the parabola are
P(at12, 2at1), Q(at22, 2at2) .
Slope of \(\overline{\mathrm{PQ}}\) is
\(\frac{2 \mathrm{at}_{2}-2 \mathrm{at}_{1}}{\mathrm{at}_{2}^{2}-\mathrm{at}_{1}^{2}}=\frac{2 \mathrm{a}\left(\mathrm{t}_{2}-\mathrm{t}_{1}\right)}{\mathrm{a}\left(\mathrm{t}_{2}^{2}-\mathrm{t}_{1}^{2}\right)}=\frac{2}{\mathrm{t}_{1}+\mathrm{t}_{2}}\)
The equation of \(\overline{\mathrm{PQ}}\) is y – 2at1 = \(\frac{2}{t_{1}+t_{2}}\) (x – at12).
⇒ (y – 2at1) (t1 + t2) = 2(x – at12)
⇒ y(t1 + t2) – 2at12 – 2at1t2 = 2x – 2at12
⇒ y(t1 + t2) = 2x + 2at1t2.
Note: If the chord joining the points t1 and t2 on the parabola y2 = 4ax is a focal chord then t1t2 = – 1.
Proof:
Equation of the parabola is y2 = 4ax
Focus S = (a, o)
The equation of the chord is y(t1 + t2) = 2x + 2at1t2
If this is a focal chord then it passes through the focus (a, 0).
∴ 0 = 2a + 2at1t2 ⇒ t1t2 = – 1.
![]()
Theorem: The point of intersection of the tangents to the parabola y2 = 4ax at the
points t1 and t2 is (at1t2, a[t2 + t2]).
Proof:
Equation of the parabola is y2 = 4ax
The equation of the tangent at t1 is yt1 = x + at12 ……. (1)
The equation of the tangent at t2 is
yt2 = x + at22 ……….. (2)
(1) – (2) ⇒ y(t1 – t2) = a(t12 – t22) ⇒ y = a(t1 + t2)
(1) ⇒ a(t1 + t2)t1 = x + at12
= at12 + at1t1 = x + at12 ⇒ x = at1t2,
∴ Point of intersection = (at1t2, a[t1 + t2]).
Theorem: Three normals can be drawn form a point (x1, y1) to the parabola y2 = 4ax.
Corollary: If the normal at t1 and t2, to the parabola y2 = 4ax meet on the parabola, then t1t2 = 2.
Proof:
Let the normals at t1 and t2 meet at t3 on the parabola.
The equation of the normal at t1 is:
y + xt1 = 2at1 + at13 ………… (1)
Equation of the chord joining t1 and t3 is:
y(t1 + t3) = 2x + 2at1t3 ……… (2)
(1) and (2) represent the same line
∴ \(\frac{t_{1}+t_{3}}{1}=\frac{-2}{t_{1}} \Rightarrow t_{3}=-t_{1}-\frac{2}{t_{1}}\)
Similarly t3 = – t1 – \(\frac{2}{\mathrm{t}_{2}}\)
∴ \(-\mathrm{t}_{1}-\frac{2}{\mathrm{t}_{1}}=-\mathrm{t}_{2}-\frac{2}{\mathrm{t}_{2}}\) ⇒ t1 – t2 \(\frac{2}{\mathrm{t}_{2}}-\frac{2}{\mathrm{t}_{1}}\)
⇒ t1 – t2 = \(\frac{2\left(\mathrm{t}_{1}-\mathrm{t}_{2}\right)}{\mathrm{t}_{1} \mathrm{t}_{2}}\) ⇒ t1t2 = 2