Practicing the Intermediate 2nd Year Maths 2B Textbook Solutions Inter 2nd Year Maths 2B Parabola Solutions Exercise 3(a) will help students to clear their doubts quickly.
Intermediate 2nd Year Maths 2B Parabola Solutions Exercise 3(a)
I.
Question 1.
Find the vertex and focus of 4y² + 12x – 20y + 67 = 0.
Solution:
Given equation 4y² + 12x- 20y + 67 = 0
4y² – 20y = -12x – 67
y² – 5y = – 3x – \(\frac{67}{4}\)
Adding \(\frac{25}{4}\) on both sides


Question 2.
Find the vertex and focus of x2 -16x- 6y + 6 = 0.
Solution:
Given equation is
x² – 6x – 6y + 6 = 0
x² – 6x = 6y – 6
Adding 9 on both sides
x² – 6x + 9 = 6y + 3

Question 3.
Find the equations of axis and directrix of the parabola y² + 6y – 2x + 5 = 0.
Solution:
y² + 6y = 2x – 5
Adding ‘9’ on both sides we get,
y² + 6y + 9 = 2x – 5 + 9
[y – (-3)]² = 2x + 4
[y – (-3)]² = 2[x – (-2)]
Comparing with (y – k)² = 4a (x- h) we get,
(h, k) – (-2, -3), a = \(\frac{1}{2}\)
Equation of the axis y – k = 0 i.e. y + 3 = 0
Equation of the directrix x – h + a = 0
i.e., x – (-2) + \(\frac{1}{2}\) = 0
2x + 5 = 0.
![]()
Question 4.
Find the equation of axis and directrix of the parabola 4x² + 12x – 20y + 67 = 0.
Solution:
4x² + 12x = 20y – 67
x² + 3x = 5y – \(\frac{67}{4}\)
Adding \(\frac{9}{4}\) on both sides we get
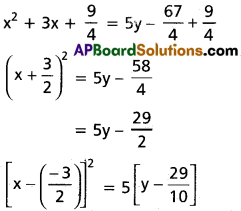
Comparing with (x – h)² = 4a(y – k)
(h, k) = (\(\frac{-3}{2},\frac{29}{10}\)) ; a = \(\frac{5}{4}\)
Equation of the axis x – h = 0, i.e., x + \(\frac{3}{2}\) = 0
2x + 3 = 0
Equation of the directrix, y – k + a = 0
y – \(\frac{29}{10}\) + \(\frac{5}{4}\) = 0
⇒ 20y – 33 = 0.
Question 5.
Find the equation of the parabola whose focus is S (1, -7) and vertex is A(1, -2).
Solution:
Let S = (1, -7), A(1, -2)
h = 1, k = -2, a = -2 + 7 = 5
Axis of the parabola is parallel to y-axis Equation of the parabola is
(x – h)² = -4a (y – k)
(x – 1)² = – 20(y + 2)
x² – 2x + 1 = – 20y – 40
⇒ x² – 2x + 20y + 41 = 0.
Question 6.
Find the equation of the parabola whose focus is S(3, 5) and vertex is A(1, 3).
Solution:
Equation of the axis y – 3 = \(\frac{3-5}{1-3}\) (x – 1)
= x – 1
x – y + 2 = 0
The directrix is perpendicular to the axis. Equation of the directrix is x + y + k = 0
Co-ordinates of Z be (x, y)
A is the midpoint of SZ
Co-ordinates of A are \(\frac{3+x}{2},\frac{5+y}{2}\)) = (1, 3)
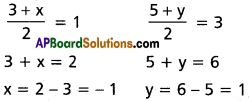
Co-ordinates of Z are (-1, 1)
The directrix passes through Z (-1, 1)
-1 + 1 + k = 0 ⇒ k = 0
Equation of the directrix is x – y = 0
Equation of the parabola is

⇒ 2(x² – 6x + 9 + y2 – 10y + 25) = (x + y)²
⇒ 2x² + 2y² – 12x – 20y + 68 = x² + 2xy + y²
i.e., x² – 2xy + y² – 12x – 20y + 68 = 0.
![]()
Question 7.
Find the equation of the parabola whose latus rectum is the line segment of joining the points (-3, 2) and (-3, 1).
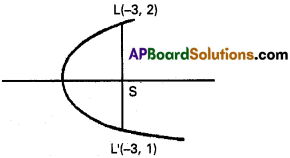
Solution:
L (-3, 2) and L(-3, 1) are the ends of the latus rectum.
S is the midpoint of LL’
Co-ordinates of S are (-3, \(\frac{3}{2}\))
LL’ = \(\sqrt{(-3+3)^{2}+(2 – 1)^{2}}=\sqrt{0+1}\) = 1
4|a| = 1, ⇒ |a| = \(\frac{1}{4}\) ⇒ a = ± \(\frac{1}{4}\)
Case (i) a = –\(\frac{1}{4}\)
Co-ordinates of A are [-3 + \(\frac{1}{4}\), \(\frac{3}{2}\)]
Equation of the parabola is
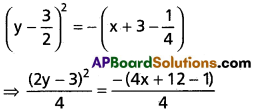
(2y – 3)² = -(4x + 11)
Case (ii) a = –\(\frac{1}{4}\)
Co-ordinates of A are [-3 – \(\frac{1}{4}\), \(\frac{3}{2}\)]
Equation of the parabola is
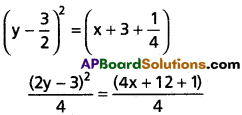
i.e., (2y – 3)² = 4x + 13.
Question 8.
Find the position (interior or exterior or on) of the following points with respect to the parabola y² = 6x,
i) (6, -6)
Solution:
Equation of the parabola is
y² = 6x
i.e., S ≡ y² – 6x
S11 = (-6)² – 6.6 = 36 – 36 = 0
∴ (6, – 6) lies on the parabola.
ii) (0,1)
S11 = 1² – 6.0 = 1 > 0
∴ (0, 1) lies outside the parabola.
iii) (2, 3)
S11 = 32 – 6.2
= 9 – 12
= – 3 < 0
∴ (2, 3) lies inside the parabola.
Question 9.
Find the co-ordinates of the point on the parabola y² = 8x whose focal distance is 10.
Solution:
Equation of the parabola is y² = 8x
4a = 8 ⇒ a = 2

Co-ordinates of the focus S are (2, 0)
Suppose P(x, y) is the point on the parabola.
Given SP = 10 ⇒ SP² = 100
(x – 2)² + y2 = 100
But y² = 8x
⇒ (x – 2)² + 8x = 100
⇒ x² – 4x + 4 + 8x – 100 = 0
⇒ x² + 4x – 96 = 0 ⇒ (x + 12) (x – 8) = 0
x + 12 = 0 or x – 8 = 0
x = -12, or 8
Case (i) x = 8
y² = 8.x = 8.8 = 64
y = ±8
Co-ordinates of the required points are (8, 8) and (8, -8)
Case (ii) x = -12
y² = 8(-12) = -96 < 0
y is not real.
![]()
Question 10.
If (\(\frac{1}{2}\), 2) j is one extermity of a focal chord of the parabola y² = 8x. Find the co-ordinates of the other extremity.
Solution:
A = \(\frac{1}{2}\), 2); S = (2, 0)
B = (x1, y1) ⇒ (\(\frac{y^{2}_{2}}{8}\), y1)
ASB is a focal chord.
∴ Slopes of SA and BS are same.
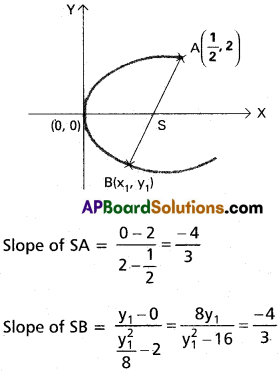
24y1 = -4y²1 + 64
or 4y²1 + 24y1 – 64 = 0
⇒ y²1 + 6y1 – 16 = 0 ⇒ (y1 + 8) (y1 – 2) = 0
y1 = 2, -8
x1 = \(\frac{1}{2}\), 8; So (8, -8) other extremity.
Question 11.
Prove that the parabola y2 – 4ax, (a > O) Nearest to the focus is its vertex.
Solution:
Let P(at², 2at) be the point on the parabola y² = 4ax, which is nearest to the
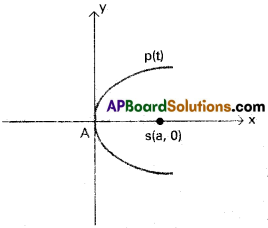
focus S(a, 0) then
fSp²= (at² – a)² + (2at – 0)²
f(t) = a²2(t² – 1)(2t) + 4a²(2t)
= 4a²t(t² – 1 + 2) = 4a²t(t² + 1)
For minimum value of f(t) = 0 ⇒ t = 0
f”(L) = 4a²(3t² +1) s
f(0) = 4a² > 0
∴ At t-= 0, f(t) is minimum Then P = (0, 0)
∴ The point on the parabola y² = 4ax, which is nearest to the focus is its vertex A(0, 0).
Question 12.
A comet moves in a Parabolic orbit with the sun as focus when the comet is 2 × 107 K.M from the sun, the line from the sun to it makes an fmgle \(\frac{\pi}{2}\) with the axis of the orbit. Find how near the comet comes to the sun.
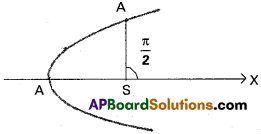
Solution:
Suppose the equation of the parabolic orbit of the comet is y² = 4ax
P is the position of the comet.
Given ∠XSP = \(\frac{\pi}{2}\)
SP is perpendicular to the axis of the parabola.
SP is the semi-latus rectum
2a = 2 × 107
⇒ a = 107 km
A is the nearest point on the parabola from focus.
AS = a = 107 km
∴ The nearest point on the parabola is 107 km from the sun.
II.
Question 1.
Find the locus of the points of trisection of double ordinate of a parabola y² = 4ax (a > 0).
Solution:
Equation of the parabola is y² = 4ax
P(x, y) and Q(x, -y) are the ends of the double ordinate.
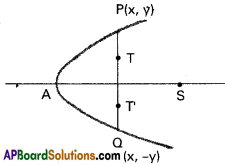
T divides PQ in the ratio 1 : 2
Co-ordinates of T are (x, \(\frac{-y+2y}{3}\))
= (x, \(\frac{y}{3}\))
T divides PQ in the ratio 2 : 1
Co-ordinates of T are (x, \(\frac{-2y+y}{3}\))
= (x, –\(\frac{y}{3}\))
Suppose Co-ordinates of the required points
L and L’ be (x1, y1)
y1 = ± \(\frac{y}{3}\) ⇒ y²1 = \(\frac{y^{2}}{9}\)
y² = 9y²1
4ax1 = 9y²1
Locus of (x1, y1) is 9y² = 4ax.
![]()
Question 2.
Find the equation of the parabola whose vertex and focus are on the positive X – axis at a distance of a and a’ from the origin respectively.
Solution:
Given Co-ordinates of A are (a, 0) and S are (a’, 0)
AS = a’ – a
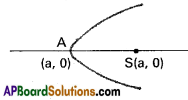
Equation of the parabola is
y² = 4(a’ – a) (x – a).
Question 3.
If L and L‘ are the ends of the latus rectum of the parabola x² = 6y, find the equations of OL and OL’ where ‘O’ is the origin. Also find the angle between them.
Solution:
x² = 6y
Curve is symmetric about Y – axis
Extremities of latus rectum are
(2a, a), (-2a, a)
4a = 6 ⇒ a = \(\frac{3}{2}\)

Question 4.
Find the equation of the parabola whose axis is parallel to X-axis and which passes through these points. (-2, 1) (1, 2), and (-1, 3)
Solution:
Axis is parallel to X – axis
General equation be
x = ay² + by + c
Passes through (-2, 1) (1, 2) (-1, 3)
-2 = a + b + c ………. (i)
1 = 4a + 2b + c ……….. (ii)
-1 = 9a + 3b + c …………. (iii)
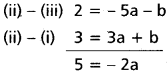
⇒ –\(\frac{5{2}\) = a
i.e., \(\frac{21}{2}\) = b
-10 = c
x = –\(\frac{5}{2}\)y² + \(\frac{21}{2}\)y – 10
5y² + 2x – 21y + 20 = 0
Question 5.
Find the equation of the parabola whose axis is parallel to Y – axis and which passes .through the points (4, 5), (-2, 11) and (-4, 21).
Solution:
General equation be y = ax² + bx + c passes through (4, 5), (-2, 11), (-4, 21) we get
5 = 16a + 4b + c ……… (i)
11 = 4a – 2b + c ……….. (ii)
21 = 16a – 4b + c ……….. (iii)
(ii) – (i) we get
6 = -12a – 6b
(iii) – (ii) 10 = 12a – 2b
Solving we get
b = -2, a = 1/2; c = 5
y = \(\frac{1}{2}\)x² – 2x + 5
x² – 2y – 4x + 10 = 0
III.
Question 1.
Find the equation of the parabola whose focus is (-2, 3) and directrix is the line 2x + 3y – 4 = 0. Also find the length of the latus rectum and the equation of the axis of the parabola.
Solution:
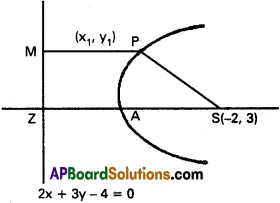
Suppose P(x1, y1) is any point on the parabola.
S(-2, 3) is the focus.
SP² = (x1 + 2)² + (y1 – 3)²
Equation of the directrix is 2x + 3y – 4 = 0
PM is the perpendicular from P on the directrix
PM = \(\frac{2x_{1}+3y_{1}-4}{\sqrt{4+9}}\)
From Def. of parabola SP = PM ⇒ SP² = PM²
(x1 + 2)² + (y1 – 3)² = \(\frac{(2x_{1}+3y_{1}-4)^{2}}{13}\)
⇒ 13(x²1 + 4x1 + 4 + y²1 – 6y1 + 9) = (2x1 + 3y1 – 4)²
⇒ 13x²1 + 13y²1 + 52x1 – 78y1 + 169
= 4x²1 + 9y²1 + 16 + 12x1y1 – 16x1 – 24y1
⇒ 9×21 – 12x1y1 + 4y²1 + 68x1 – 54y1 + 153 = 0
Locus of P(x1, y1) is
9x² – 12xy + 4y² + 68x- 54y + 153 = 0
Length of the latus rectum = 4a
Perpendicular distance from S on directrix
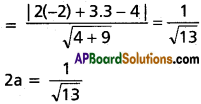
Length of the latus rectum = 4a = \(\frac{2}{\sqrt{3}}\)
The axis is perpendicular to the .directrix Equation of the directrix can be taken as
3x – 2y + k = 0
This line passes through S (-2, 3)
– 6 – 6 + k = 0 ⇒ k = 12
Equation of the axis is 3x – 2y + 12 = 0
Question 2.
Prove that the area of the triangle inscribed in the parabola y² = 4ax is \(\frac{1}{8a}\)|(y1 – y2) (y2 – y3) (y3 – y1)| sq. units where y1, y2, y3 are the ordinates of its vertices.
Solution:
Suppose P(at²1, 2at1), Q(at²2, 2at2),
R(at²3, 2at3) are the vertices of ∆PQR.
Area of ∆PQR = \(\frac{1}{2}\) | at²1 (2at2 – 2at3) + at²2 (2at3 – 2at1) + at²3(2at1 – 2at2)|
= \(\frac{1}{2}\) . 2a² |t²1 (t2 – t3) + t²2(t3 – t1) + t²3(t1 – t2)|
= a² |(t1 – t2) (t2 – t3) (t3 – t1)|
= \(\frac{1}{8a}\) |(2at1 – 2at2) (2at2 – 2at3) (2at3 – 2at1) |
= \(\frac{1}{8a}\) |(y1 – y2) (y2 – y3) (y3 – y1)|
Where P(x1, y1), Q(x2, y2), R(x3, y3) are the vertices of ∆PQR.
![]()
Question 3.
Find the co-ordinates of the vertex and focus, the equation of the directrix and axis of the -following parabolas.
(i) y² + 4x + 4y – 3 = 0
(ii) x² – 2x + 4y – 3 = 0
Solution:
i) y² + 4x + 4y – 3 = 0
⇒ y² + 4y = – 4x + 3
⇒ y² + 4y + 4 = – 4x +. 3 + 4
⇒ (y + 2)² = – 4x + 7
⇒ [y – (-2)]² = -4[x – \(\frac{7}{4}\)]
h = \(\frac{7}{4}\), k = -2, a = 1
Vertex A(h, k) = (\(\frac{7}{4}\), -2)
Focus (h-a, k) = (\(\frac{7}{4}\) – 1, -2)
= (\(\frac{3}{4}\), -2)
Equation of the directrix x – h – a = 0
x – \(\frac{7}{4}\) – 1 = 0
4x – 11 = 0
Equation of the axis is y – k = 0
y + 2 = 0
ii) x² – 2x + 4y – 3 = 0
⇒ x² – 2x = – 4y + 3
⇒ x – 2x + 1 = – 4y + 3 + 1
(x – 1)² = – 4y + 4
= – 4[y – 1 ]
(x – 1)² = – 4[y – 1]
h = 1; k = 1; a = 1
Vertex A(h, k) = (1, 1)
Focus (h, k – a) =(1, 1 -1)
= (1, 0)
Equation of the directrix
y – k – a = 0
y – 1 – 1 = 0
y – 2 = 0
Equation of the axis is,
x – h = 0
x – 1 = 0