AP 10th Class Maths Important Questions Chapter 9 వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు

These AP 10th Class Maths Chapter Wise Important Questions 9th Lesson వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు will help students prepare well for the exams.

AP Board 10th Class Maths 9th Lesson Important Questions and Answers వృత్తాలకు స్పర్శరేఖలు మరియు ఛేదనరేఖలు

ప్రశ్న 1.
క్రింది పటంలో గల వృత్తానికి a, b, భాగాలను ఏమని పిలుస్తారు ?
సాధన.

a ని అల్ప వృత్తఖండము మరియు b ని అధిక వృత్తఖండం అని పిలుస్తారు.

ప్రశ్న 2.
7 సెం.మీ. వ్యాసార్ధముగా కల్గిన వృత్త కేంద్రం నుండి 25 సెం.మీ. దూరంలో ఉన్న బిందువు నుండి గీయబడిన స్పర్శరేఖ పొడవును కనుగొనండి.
సాధన.
దత్తాంశము OA = 25 సెం.మీ.,
OB = r = 7 సెం.మీ.
∆AOB లో ∠B = 90°

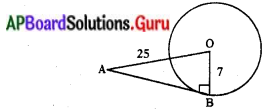
∴ OA² = OB² + AB²
⇒ AB² = OA² – OB² = 25² – 7²
⇒ AB = √(25² – 7²)
= √(625 – 49)
= √576 = 24 సెం.మీ.

ప్రశ్న 3.
4 సెం.మీ. వ్యాసార్ధం గల ఒక వృత్త కేంద్రం నుండి 5 సెం.మీ. దూరంలో ఉన్న ఒక బిందువు నుండి ఆ వృత్తానికి గీయబడిన స్పర్శరేఖ పొడవును కనుగొనుము.
సాధన.

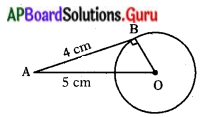
∆OAB అనునది లంబకోణ త్రిభుజము.
OA² = OB² + AB²
5² = OB² + 4²
⇒ OB² = 25 – 16 = 9
∴ OB = √9 = 3 సెం.మీ.

ప్రశ్న 4.
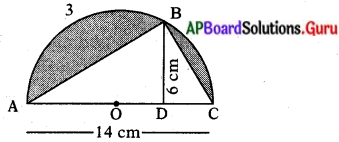
ఇవ్వబడిన పటంలో షేడ్ చేసిన ప్రాంత వైశాల్యం కనుగొనండి.

సాధన.
షేడ్ చేసిన ప్రాంత వైశాల్యం = అర్ధవృత్త వైశాల్యం – త్రిభుజ వైశాల్యం
= \(\frac{\pi \mathrm{r}^{2}}{2}\) – \(\frac{1}{2}\)bh
= \(\frac{\frac{22}{7} \times 7 \times 7}{2}\) – \(\frac{1}{2}\) × 14 × 6
= 11 × 7 – 7 × 6
= 77 – 42 = 35 చ.సెం.మీ.

ప్రశ్న 5.
7 సెం.మీ. వృత్త వ్యాసార్ధము మరియు కేంద్రం వద్ద కోణం 60° గా గల వృత్త సెక్టారు యొక్క వైశాల్యమును కనుగొనండి.
సాధన.
వ్యాసార్ధం = 7 సెం.మీ., కేంద్రం వద్ద కోణం = 60°
సెక్టారు యొక్క వైశాల్యము = \(\frac{x}{360}\) × πr
= \(\frac{60 \times \frac{22}{7} \times 7 \times 7}{360}=\frac{154}{6}\)
= 25.66 సెం.మీ.²

ప్రశ్న 6.
3 సెం.మీ. వ్యాసార్ధముతో వృత్తాన్ని గీచి, వృత్త పరిధిపై బిందువు ‘P’ ను గుర్తించి దానిగుండా పోయే స్పర్శరేఖను గీయండి.
సాధన.
నిర్మాణ క్రమము : –

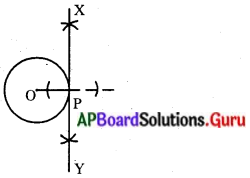
1) “O” కేంద్రముగా 3 సెం.మీ. వ్యాసార్ధముతో వృత్తమును గీచితిని. వృత్త పరిధిపై ‘P’ బిందువును గుర్తించి \(\overline{\mathrm{OP}}\)ని గీచితిని.
2) \(\overline{\mathrm{OP}}\) కు లంబంగా \(\overline{\mathrm{XY}}\) ను నిర్మించితిని.
∴ \(\overline{\mathrm{XY}} \perp \overline{\mathrm{OP}}\)
3) \(\overline{\mathrm{XY}}\) వృత్తానికి ‘P’ గుండా పోయే స్పర్శరేఖ అవుతుంది.

ప్రశ్న 7.
3 సెం.మీ. వ్యాసార్థం గల వృత్తాన్ని గీయండి. దాని కేంద్రం నుండి 5 సెం.మీ. దూరంలో ‘P’ అనే బిందువును గుర్తించి, P నుండి వృత్తానికి 2 స్పర్శరేఖలు గీయండి.
సాధన.
నిర్మాణక్రమం : .
i) 3 సెం.మీ. వ్యాసార్ధంతో వృత్తం గీయుము.

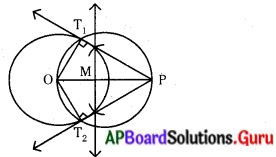
ii) 0 నుండి 5 సెం.మీ. దూరంలో P గుర్తించి, OP ని కలుపుము.
iii) OPను లంబ సమద్వి ఖండన చేయగా అది OP ని Mవద్ద ఖండించినచో M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీయుము.
iv) వృత్తాల ఖండన బిందువుల నుండి స్పర్శరేఖలు గీయుము.

ప్రశ్న 8.
4 సెం.మీ. వ్యాసార్ధముతో ఒక వృత్తాన్ని గీయండి. కేంద్రము నుండి 7.5 సెం.మీ. దూరములో గల బిందువు నుండి ఒక జత, స్పర్శరేఖలు గీయండి.
సాధన.
నిర్మాణ క్రమము :

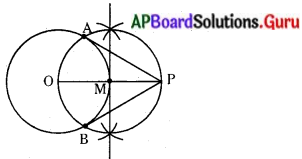
1) 0 కేంద్రంగా 4 సెం.మీ. వ్యాసార్ధముతో వృత్తంను గీయుము.
2) 0 కేంద్రంగా 7.5 సెం.మీ. దూరంలో P బిందువును గుర్తించి, OP ని కలుపుము.
3) OP ను లంబ సమద్విఖండన చేసి M ను గుర్తించి
M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీయుము.
4) P నుండి వృత్తాల ఖండన బిందువులకు స్పర్శరేఖలు CPA మరియు PB గీయుము.

ప్రశ్న 9.
5 సెం.మీ. వ్యాసార్థము గల వృత్తమును గీచి, వృత్త కేంద్రము నుండి 8 సెం.మీ. దూరములో గల బిందువు నుండి ఒక జత స్పర్శరేఖలను నిర్మించుము.
సాధన.

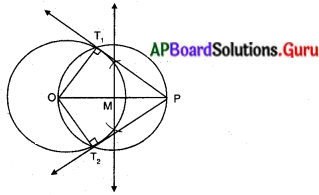
నిర్మాణము :
1) ‘O’ కేంద్రముగా 5 సెం.మీ. వ్యాసార్ధంతో వృత్తం గీచితిని.
2) ‘0’ నుండి 8 సెం.మీ. దూరంలో ‘P’ గుర్తించి, OP ని కలిపితిని.
3) OP ను లంబ సమద్విఖండన చేయగా అది OPని ‘M’ వద్ద ఖండించినది. M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీచితిని.
4) P నుండి వృత్తాల ఖండన బిందువులైన T, , T, లకు స్పర్శరేఖలు PT, మరియు PT, లను గీచితిని.

ప్రశ్న 10.
4 సెం.మీ. వ్యాసార్ధంతో ఒక వృత్తాన్ని గీయండి. కేంద్రం నుండి 6 సెం.మీ. దూరములో గల బిందువు వద్ద ఖండించుకొనునట్లు ఒక జత స్పర్శరేఖలను గీయండి. .
సాధన.

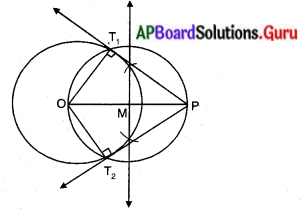
నిర్మాణ క్రమము :
i) 0 కేంద్రముగా 4 సెం.మీ. వ్యాసార్ధంతో వృత్తం గీచితిని.
ii) 0 నుండి 6.సెం.మీ. దూరంలో P గుర్తించి, OP కలిపితిని.
iii)OPను లంబ సమద్విఖండన చేయగా అది OPని M వద్ద ఖండించును. M కేంద్రంగా MO లేదా MP వ్యాసార్ధంతో వృత్తం గీచితిని.
iv)వృత్తాల ఖండన బిందువుల నుండి స్పర్శరేఖలు గీచితిని.

ప్రశ్న 11.
కింది పటం ‘O’ కేంద్రంగా గల వృత్తంలో PQ = 12 సెం.మీ., PR = 5 సెం.మీ., వ్యాసం QR అయిన షేడ్ చేయబడిన ప్రాంత వైశాల్యాన్ని కనుగొనండి. (ఇక్కడ TT = 22 గా తీసుకొనుము)

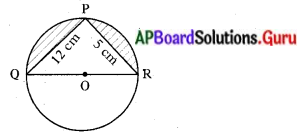
సాధన.
ఇక్కడ ‘PQ’ = 12 సెం.మీ.
‘PR’ = 5 సెం.మీ.
‘QR’ వ్యాసము
PQOR ఒక అర్ధవృత్తము అర్ధవృత్తములో కోణము = 90°.
∴ ∆QPR = 90°
∴ ∆POR ఒక లంబకోణ త్రిభుజము .
∴ ∆PQR వైశాల్యము = \(\frac{1}{2}\) bh
= \(\frac{1}{2}\) × PQ × PR
= \(\frac{1}{2}\) × 12 × 5 = 30 సెం.మీ² …………..(1)
షేడ్ చేయబడిన వృత్తఖండ వైశాల్యం = అర్ధవృత్త వైశాల్యం – ∆PQR వైశాల్యం
= \(\frac{1}{2}\) πr² – 30 సెం.మీ.² . ………(2)
∆PQR లో QR² = PQ² + PR²2 (పైథాగరస్ సిద్ధాంతం నుండి)
QR²2 = 12² + 5²
= 144 + 25 = 169 = 13²
∴ QR = 13
వృత్త వ్యాసార్ధము (r) = QO = \(\frac{\mathrm{QR}}{2}\)
= \(\frac{13}{2}\) = 6.5 సెం.మీ.
అర్ధవృత్త వైశాల్యము = \(\frac{1}{2}\) πr²
= \(\frac{1}{2}\) × \(\frac{22}{7}\) × \(\frac{13}{2}\) × \(\frac{13}{2}\)
= 66.39 సెం.మీ.² ………..(3)
(1) మరియు (3) లను (2) లో ప్రతిక్షేపించగా
∴ షేడ్ చేయబడిన వృత్తఖండ వైశాల్యం
= (66.39 – 30)
= 36.39 సెం.మీ.²