AP 10th Class Maths Important Questions Chapter 10 క్షేత్రమితి

These AP 10th Class Maths Chapter Wise Important Questions 10th Lesson క్షేత్రమితి will help students prepare well for the exams.

AP Board 10th Class Maths 10th Lesson Important Questions and Answers క్షేత్రమితి

ప్రశ్న 1.
7 సెం.మీ. వ్యాసార్ధం గల అర్ధగోళ సంపూర్ణతల – వైశాల్యంను కనుగొనుము.
సాధన.
అర్ధగోళం వ్యాసార్ధం r = 7 సెం.మీ.
అర్ధగోళ సంపూర్ణతల వైశాల్యం = 3πr²
= 3 × \(\frac{22}{7}\) × 7 × 7
= 462 చ. సెం.మీ.

ప్రశ్న 2.
3 సెం.మీ. వ్యాసార్ధము మరియు 14 సెం.మీ. ఎత్తు కల్గిన క్రమ వృత్తాకార శంఖువు యొక్క ఘనపరిమాణం కనుగొనండి.
సాధన.
శంఖువు ఘనపరిమాణం = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 14
= 132 సెం.మీ.³

ప్రశ్న 3.
7 సెం.మీ. వ్యాసార్ధము మరియు 10 సెం.మీ. ఎత్తు కలిగిన స్థూపం యొక్క వక్రతల వైశాల్యము కనుగొనండి.
సాధన.
2స్థూపం యొక్క వ్యాసార్ధము (r) = 7 సెం.మీ.
ఎత్తు (h) = 10 సెం.మీ. స్థూపం యొక్క వక్రతల వైశాల్యం = 2πrh
= 2 × \(\frac{22}{7}\) × 7 × 10
= 440 చ.సెం.మీ.

ప్రశ్న 4.
ఒక ఫుట్ బాల్ యొక్క ఉపరితల వైశాల్యము 616 చ.సెం.మీ. అయిన ఆ బంతి వ్యాసార్ధమును కనుగొనుము. (π = 22/7)
సాధన.
ఒక ఫుట్ బాల్ యొక్క ఉపరితల వైశాల్యము (గోళం) = 4πr²
4πr² = 616
πr² = 154
r² = 154 × \(\frac{7}{22}\)
r² = 7 × 7 = 49
∴ r = 7 సెం.మీ.

ప్రశ్న 5.
ఒక స్థూపము యొక్క ఘనపరిమాణము 4481 సెం.మీ. 3 మరియు ఎత్తు 7 సెం.మీ. అయిన స్థూపము యొక్క వ్యాసార్ధము కనుగొనుము.
సాధన.
స్థూపము ఘనపరిమాణము = πr²h = 448π
ఇచ్చట h = 7 సెం.మీ. , r = r
πr² × 7 = 448π
7r² = 448
r² = \(\frac{448}{7}\) = 64
∴ వ్యాసార్ధము (r) = 8 సెం.మీ.

ప్రశ్న 6.
ఒక గోళము యొక్క వ్యాసార్ధము 14 సెం.మీ. అయిన దాని ఉపరితల వైశాల్యం కనుగొనుము. (π = \(\frac{22}{7}\) గా తీసుకొనుము)
సాధన.
గోళము యొక్క వ్యాసార్ధము = (r) = 14 సెం.మీ.
గోళఉపరితల వైశాల్యమునకు సూత్రము = 4πr²
∴ గోళ ఉపరితల వైశాల్యము = 4 × \(\frac{22}{7}\) × 14 × 14
= 88 × 28
= 2464 సెం.మీ.²

ప్రశ్న 7.
సమాన భూ వ్యాసార్ధము కలిగిన శంఖువు మరియు స్టూపములను జతగా కలుపగా ఏర్పడే ఘనాకార వస్తువు యొక్క చిత్తు పటమును గీయుము.
సాధన.

శంఖువు మరియు స్థూపముల సమాన భూవ్యాసార్ధము = AB

ప్రశ్న 8.
7 సెం.మీ. వ్యాసార్ధం, 14 సెం.మీ. ఏటవాలు ఎత్తు కలిగిన ఒక శంఖాకార జోకర్ క్యాప్ తయారు చేయడానికి అవసరమైన పేపర్ షీటు యొక్క వైశాల్యం కనుగొనండి.
సాధన.
దత్తాంశం ప్రకారం, వ్యాసార్ధం = 7 సెం.మీ.
ఏటవాలు ఎత్తు = 14 సెం.మీ.
పేపర్ షీటు యొక్క వైశాల్యం = πrl
= \(\frac{22}{7}\) × 7 × 14
= 22 × 14 = 308 సెం.మీ.²

ప్రశ్న 9.
ఒక గోళం యొక్క వ్యాసం, ఘనం యొక్క భుజంకు సమానం అయితే, వాటి ఘనపరిమాణాల నిష్పత్తిని కనుగొనుము.
సాధన.
గోళం యొక్క వ్యాసం = d = ఘనం యొక్క భుజం అనుకొనుము.
∴ గోళం యొక్క వ్యాసార్ధం (r) = \(\frac{d}{2}\),
గోళం యొక్క ఘనపరిమాణం = \(\frac{4}{3}\) πr³
= \(\frac{4}{3} \pi\left(\frac{d}{2}\right)^{3}=\frac{4}{3} \pi \frac{d^{3}}{8}=\frac{\pi}{6} d^{3}\)
మరియు ఘనం యొక్క ఘనపరిమాణం = d³
∴ గోళం ఘనపరిమాణం మరియు ఘనం ఘనపరిమాణాల నిష్పత్తి = \(\frac{\pi}{6}\)d³ : d³
= \(\frac{\pi}{6}\) : 1

ప్రశ్న 10.
125 ఘనపు సెం.మీ. ఘనపరిమాణం గల రెండు 1 ఘనములు కలుపబడినవి. అప్పుడు ఏర్పడిన దీర్ఘ ఘనము యొక్క సంపూర్ణతల వైశాల్యం ఎంత ?
సాధన.
ఒక ఘనము యొక్క ఘనపరిమాణము = 125 సెం.మీ³
a³ = 125 సెం.మీ.³ = (5 సెం.మీ)³.
∴ ఆ ఘనం యొక్క భుజం = 5 సెం.మీ.
అటువంటి రెండు ఘనములు కలుపబడినపుడు ఏర్పడిన దీర్ఘఘనం యొక్క పొడవు (l) = 10 సెం.మీ.
వెడల్పు (b) = 5 సెం.మీ.
ఎత్తు (h) = 5 సెం.మీ.

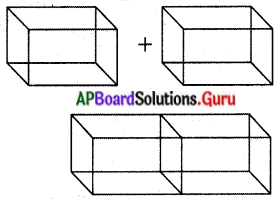
∴ దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2 (lb + bh + lh)
= 2[(10 × 5) + (5 × 5) + (5 × 10)]
= 2[50 + 25 + 50]
= 2(125) = 250 సెం.మీ²
∴ రెండు ఘనములు కలుపగా ఏర్పడిన దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 250 సెం.మీ²

ప్రశ్న 11.
ఒక శంకువు యొక్క భూ వైశాల్యం 616 చ.సెం.మీ., దాని ఎత్తు 48 సెం.మీ. అయిన దాని సంపూర్ణతల వైశాల్యం కనుగొనుము.
సాధన.
శంఖువు భూ వ్యాసార్ధం = r సెం.మీ. అనుకొనుము.
మరియు ఎత్తు = h = 48 సెం.మీ.
∴ శంఖువు భూ వైశాల్యం = πr²

= \(\frac{22}{7}\) × r² = 616 సెం.మీ²
⇒ r² = \(\frac{616 \times 7}{22}\)
= 28 × 7
= 2 × 7 × 2 × 7 = 142
∴ శంఖువు భూ వ్యాసార్ధం r = 14 సెం.మీ.
∴ శంఖువు ఏటవాలు ఎత్తు (l) = \(\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}\)
= \(\sqrt{14^{2}+48^{2}}\)
= \(\sqrt{196+2304}=\sqrt{2500}\)
∴ l = 50 సెం.మీ.
శంఖువు సం||తల వైశాల్యము = నేల వైశాల్యము + ప్రక్కతల వైశాల్యము
= πr² + πrl
= πr(r + l)
= \(\frac{22}{7}\) × 14 × (14 + 50)
= \(\frac{22}{7}\) × 14 × 64
= 44 × 64 = 2816
∴ ఆ శంఖువు సం||తల వైశాల్యము = 2816 సెం.మీ²

ప్రశ్న 12.
ఒక శంఖువు యొక్క శీర్షకోణములో, సగము 60° మరియు దాని ఎతు 3 సెం.మీ. అయిన శంఖువు యొక్క ఘనపరిమాణం కనుగొనుము.
సాధన.
‘B’ అనేది శంఖువు భూ కేంద్రము మరియు
వ్యాసార్ధము = BC
నిలువుటెత్తు AB = 3 సెం.మీ.
∠BAC = 60° అని ఇవ్వబడింది.

∆ABC ఒక లంబకోణ త్రిభుజం,
tan 60° = \(\frac{\mathrm{BC}}{\mathrm{AB}}\)
⇒ √3 = B
⇒ BC = 3√3 ‘సెం.మీ.
ఇచ్చట h = 3 సెం.మీ., r = 3√3 సెం.మీ.
శంఖువు ఘనపరిమాణం = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) π(3√3)² × 3
= 27 πసెం.మీ³
(లేదా)
= \(\frac{594}{7}\) = 84.86 సెం.మీ.³

ప్రశ్న 13.
ఒక దీర్ఘ ఘనము యొక్క పొడవు, వెడల్పు, ఎత్తులు వరుసగా (log 125 + log 8), (log 1000 – log 10) మరియు log 10 అయినచో దాని సంపూర్ణతల వైశాల్యము ఎంత ?
సాధన. దీర్ఘఘనము పొడవు (1) = (log 125 + log 8)
దీర్ఘఘనము వెడల్పు (b) = (log 1000 – log 10)
దీర్ఘఘనము ఎత్తు (h) = log 10
∴ (l) = log (125 × 8)
= log 1000
= log 10³ = 3 log 10 = 3
(b) = log 1000 – log 10
= log \(\frac{1000}{10}\)
= log 100
= log 10² = 2
(h) = log 10 = 1
దీర్ఘఘనం యొక్క సంపూర్ణతల వైశాల్యము = 2(lb + bh + lh)
= 2 (3 × 2 + 2 × 1 + 1 × 3)
= 2 (6 + 2 + 3)
= 2(11) = 22 చ|| యూనిట్లు.

ప్రశ్న 14.
ఒక గోళం యొక్క వ్యాసార్థం 3.5 సెం.మీ. దాని ఉపరితల వైశాల్యం కనుగొనుము.
సాధన.
దత్తాంశం ప్రకారం r = 3.5 సెం.మీ.
గోళం యొక్క ఉపరితల వైశాల్యం = 4πr²
= 4 × \(\frac{22}{7}\) × 3.5 × 3.5
= \(\frac{88 \times 12.25}{7}\)
= 154 సెం.మీ.²

ప్రశ్న 15.
ఒక శంఖువు యొక్క ఘపరిమాణాన్ని అదే ఆధారం మరియు ఎత్తును కలిగిన క్రమవృత్తాకార స్థూపం యొక్క ఘనపరిమాణంలో వ్యక్తీకరించి నీవు దానిని ఎలా చేరుకున్నావో వివరించండి.
సాధన.
శంఖువు యొక్క ఘనపరిమాణం = \(\frac{1}{3}\) πr²h
స్థూపం యొక్క ఘనపరిమాణం = πr²h అని మనకు తెలుసు.
కావున, శంఖువు ఘనపరిమాణం : స్థూపం ఘనపరిమాణం = \(\frac{1}{3}\) πr² : πr²h
∴ శంఖువు ఘనపరిమాణం = \(\frac{1}{3}\) × స్థూపం ఘనపరిమాణం.

ప్రశ్న 16.
శంఖాకారంలో ఉన్న గుడారం భూ వ్యాసార్థం 5 మీ. దాని ఎత్తు 12 మీ. ఆ గుడారం నిర్మించుటకు కావలసిన గుడ్డ వెడల్పు 2 మీ. అయినపుడు పొడవెంత ?
సాధన.
శంఖాకారపు గుడారము వ్యాసార్ధము (r) = 5 మీ.
గుడారము ఎత్తు (h) = 12 మీ.
∴ శంఖువు వాలు ఎత్తు (l) = \(\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}\)
= \(\sqrt{5^{2}+12^{2}}\)
= \(\sqrt{25+144}=\sqrt{169}\) = 13 మీ.
గుడారపు ప్రక్కతల వైశాల్యం = πrl .
= \(\frac{22}{7}\) × 5 × 13 = \(\frac{1430}{7}\) చ.మీ.
ఉపయోగింపబడిన కొన్వాసు గుడ్డ ‘వైశాల్యం = \(\frac{1430}{7}\) చ.మీ.
కాన్వాసు గుడ్డ వెడల్పు 2 మీ. అని ఇవ్వబడింది.
కనుక కాన్వాసు గుడ్డ పొడవు = వైశాల్యము / వెడల్పు
= \(\frac{1430}{7} \times \frac{1}{2}\) = 102.14 మీ.

ప్రశ్న 17.
66 సెం.మీ. భుజము కొలతగా గల ఒక సీసపు ఘనమును 3 సెం.మీ. వ్యాసార్ధము కల్గిన ఎన్ని గోళాకార బంతులుగా మార్చవచ్చు ? ”
సాధన.
ఘనం యొక్క భుజము (s) = 66 సెం.మీ.
గోళాకార బంతి వ్యాసార్ధము (r) = 3 సెం.మీ.
తయారుచేయగల గోళాకార బంతుల సంఖ్య = n అనుకొనుము.
n × గోళాకార బంతి ఘనపరిమాణం = ఘనం ఘనపరిమాణం
⇒ n × \(\frac{4}{3}\)πr³ = s³
⇒ n × \(\frac{4}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 3 = (66)³
⇒ n = 66 × 66 × 66 × \(\frac{3}{4} \times \frac{7}{22} \times \frac{1}{3} \times \frac{1}{3} \times \frac{1}{3}\)
∴ n = 2541
తయారుచేయగల గోళాకార బంతుల సంఖ్య = 2541.

ప్రశ్న 18.
స్థూపాకృతిలో ఉన్న ‘నూనె పీపా 2 మీ. భూవ్యాసం మరియు 7 మీ. ఎత్తును కల్గియున్నది. పీపాకు రంగు వేయడానికి పెయింటర్ 1 చ.మీ. కు .₹ 5 లను తీసుకుంటుంటే, 10 నూనె పీపాలకు రంగు వేయడానికి ఎంత ఖర్చు అవుతుంది ?
సాధన.

స్థూపాకృతిలో ఉన్న నూనె పీపా భూ వ్యాసం = d = 2 మీ.
పీపా వ్యాసార్ధం = r= 2
ఎత్తు = h = 7 మీ.
స్థూపాకార నూనె పీపా యొక్క సంపూర్ణతల వైశాల్యం = 2πr(r + h)
= 2 × \(\frac{22}{7}\) × 1 × (1 + 7)
= 2 × \(\frac{22}{7}\) × 8
= \(\frac{352}{7}\) = 50.28 చ.మీ.
1 చ.మీ.కు రంగు వేయుటకు ఖర్చు = రూ. 5 అటువంటి 10 పీపాలకు రంగు వేయడానికి అయ్యే ఖర్చు = 50.28 × 5 × 10 = రూ. 2514

ప్రశ్న 19.
ఒక సమ ఘనాకార చెక్కదిమ్మ నుండి దాని భుజము పొడవునకు సమాన పొడవు వ్యాసముగా కల్గిన అర్ధగోళము కత్తిరించబడినది. ఘనము యొక్క అంచు. పొడవు 21 సెం.మీ. అయిన మిగిలిన చెక్కదిమ్మ యొక్క సంపూర్ణతల వైశాల్యము కనుగొనుము.
సాధన.
అర్ధగోళం వ్యాసము = 1 = 21 సెం.మీ. అనుకొనుము
అర్ధగోళం వ్యాసార్థం = \(\frac{l}{2}=\frac{21}{2}\) సెం.మీ.
ఘనపు అంచు పొడవు = l = 21. సెం.మీ.
మిగిలిన చెక్కదిమ్మ సంపూర్ణతల వైశాల్యం =

ప్రశ్న 20.
6 సెం.మీ., 8 సెం.మీ. వ్యాసార్ధాలు కలిగిన రెండు లోహపు గోళాలను మరొక గోళముతో కలిపి కరిగించి ఒక పెద్ద గోళంగా తయారు చేయగా, దాని వ్యాసార్ధము 12 సెం.మీ. అయినది. అయిన మూడవ గోళము యొక్క వ్యాసార్ధము కనుగొనుము.
సాధన.
రెండు గోళాల వ్యాసార్ధాలు = r₁ = 6 సెం.మీ.
r₂ = 8 సెం.మీ.
గోళాల ఘనపరిమాణాలు = \(\frac{4}{3}\) πr₁³, \(\frac{4}{3}\) πr₂³
∴ పెద్ద గోళము యొక్క ఘనపరిమాణం = \(\frac{4}{3}\) π(r₁³ + r₂³)
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × (6³ + 8³)
= \(\frac{4}{3}\) × \(\frac{22}{7}\) × 728 ………….. (1)
మూడవ గోళము వ్యాసార్ధము= ‘x’ సెం.మీ. అనుకొనిన మూడింటితో తయారైన గోళ ఘనపరిమాణం
= \(\frac{4}{3}\) π(r₁³ + r₂³ + x³)
= \(\frac{4}{3}\) × \(\frac{22}{7}\) (728 + x³) …………………..(2)
పెద్ద గోళం వ్యాసార్ధము = 12 సెం.మీ.
పెద్ద గోళం ఘనపరిమాణం = \(\frac{4}{3}\) π.12³
∴ (2) = (3)
\(\frac{4}{3}\) × \(\frac{22}{7}\) (728 + x³) = \(\frac{4}{3}\) × \(\frac{22}{7}\) × 12³
⇒ 728 + x³ = 12³
⇒ x³ = 12³ – 728
= 1728 – 728
= 1000 సెం.మీ.
⇒ x = 10 సెం.మీ.

ప్రశ్న 21.
ఒక్కొక్కటి 216 ఘనపు సెం.మీ. ఘనపరిమాణము గల రెండు ఘనములు కలుపబడినవి అయిన ఏర్పడిన కొత్త దీర్ఘ ఘనము యొక్క సంపూర్ణ తల వైశాల్యము ఎంత ?
సాధన.
దత్తాంశం ప్రకారం, ఘనం యొక్క ఘనపరిమాణం V = a³ = 216 సెం.మీ³
∴ a³ = 6 × 6 × 6 = 6³
కావున, a = 6 సెం.మీ. –

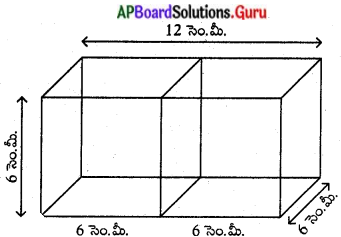
రెండు ఘనములను కలిపినపుడు, దీర్ఘఘనము యొక్క పొడవు = 2a = 2 × 6 = 12 సెం.మీ.,
వెడల్పు = a = 6 సెం.మీ.,
ఎత్తు = a = 6 సెం.మీ.
∴ దీర్ఘ ఘనం యొక్క సంపూర్ణతల వైశాల్యం = 2(lb + bh + th)
= 2(12 × 6 + 6 × 6 + 12 × 6)
= 2(72 + 36 + 72) = 2 × 180
= 360 సెం.మీ.²
∴ కొత్తగా ఏర్పడిన దీర్ఘ ఘనము యొక్క సంపూర్ణతల వైశాల్యం 360 సెం.మీ.²