AP 7th Class Maths Notes 11th Lesson Area of Plane Figures

Students can go through AP Board 7th Class Maths Notes 11th Lesson Area of Plane Figures to understand and remember the concept easily.

AP Board 7th Class Maths Notes 11th Lesson Area of Plane Figures

→ Aryabhatta (476-550 AD):
The great Indian mathematician Aryabhatta calcul¬ated the value of V (pie) at 3.1416. In Ganitapada 6, Aryabhatta given the formula to find area of a triangle as ‘Tribhujasya Phalasariram Samadalakoti Bhujardhasamvargah’ that translates to ‘For a triangle, the result of a perpendicular with the half side is the area’.

→ Area of Triangle:

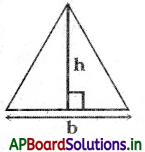
Area of Triangle = \(\frac{1}{2}\) × base × height
= \(\frac{1}{2}\) × b × h

→ Area of a right-angled triangle:

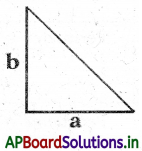
Area of a right-angled triangle = \(\frac{1}{2}\) product of sides forming the right angle
= \(\frac{1}{2}\)a × b

→ The area of the rectangular path
= Area of outer rectangle ABCD – Area of inner rectangle EFGH
= (L × B) – (l × b)

Note: If path is out side the rectangle of length (Z), breadth (b) then L = l + 2w, B = b + 2w.
If path is inside the rectangle of length (L), breadth (B)
then l = L – 2w, b = B – 2w.

→ Area of square:

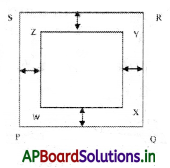
The Area of square path = Area of outer square PQRS – Area of inner square WXYZ.

→ Area of shaded portion:

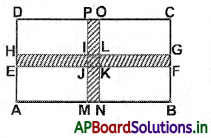
Area of shaded portion = Area of EFGH + Area of MNOP – Area of IJKL

→ Area of Circle:

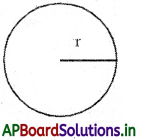
The area of the circle A = πr²

→ Area of Circular Path:

The area of circular path = Area of outer circle – Area of inner circle
= πR² – πr²
= π(R² – r²)
= π(R + r)(R – r) sq.unit.s
Note: If inner circle radius ‘r’ and width of path ‘w’ are given then outer circle radius ‘R’ = (r + w)

→ Area Formula: The area of a closed geometric figure is the measurement of space en¬closed by it. Area formula .for polygons can be represented using algebraic expressions.

→ Perimeter Formula: A Perimeter is the length of the boundary of a closed geometric figure. Algebraic expressions can be used to represent the perimeter formula for the regular polygons.

→ Area of the rectangular path:
We will use the formula Area of rectangle = l × b, where l is the length of the rectangle and b is the breadth of the rectangle.

→ Complete step-by-step answer:
From the figure, we can observe that the area of the path is the difference in the area of the bigger rectangle and the smaller rectangle.

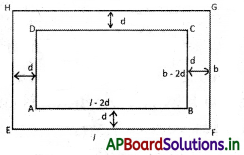
Let the length of the outer rectangle = L
And the breadth of the outer rectangle = B
A path of width w is laid inside around the rectangle.

In the figure width of the path is denoted by d.
Sometimes we denote it by w.
Then, the length of the inner rectangle = l = (L – 2w)
And the breadth of the inner rectangle = b = (B – 2w)
Area of path = area of outer rectangle – area of inner rectangle = L.B – (L – 2w)(B – 2w)

If the path is laid outside and around a rectangle of dimensions l and b,
then, the length of the outer rectangle = L = (l + 2w)
And the breadth of the outer rectangle = B = (b + 2w)
Area of path = area of outer rectangle – area of inner rectangle = (l + 2w)(b + 2w) – lb

Example:
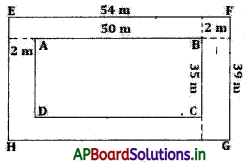
A rectangular lawn of length 50 m and breadth 35 m is to be surrounded externally by a path which is 2 m wide. Find the cost of turfing the path at the rate of Rs.3 per m².

Answer:
Length of the lawn = 50 m
Breadth of the lawn = 35 m
Area of the lawn = (50 × 35) m² = 1750 m².

Length of lawn including the path = [50 + (2 + 2)] m = 54 m
Breadth of the lawn including the path [35 + (2 + 2)] m = 39 m
Area of the lawn including the path = 54 × 39 m² = 2106 m²

Therefore, area of the path = (2106- 1750) m² = 356 m²
For 1 m², the cost of turfing the path = Rs. 3
For 356 m², the cost of turfing the path = Rs.3 × 356 = Rs. 1068
Area of Square path: We will use the # formula Area of square = s × s, where s is the side of the square.

From the figure, we can observe that the area of the path is the difference in the area of the bigger square and the smaller square.

Let the side of the outer square = s
A path of width w is laid inside around the square.

In the figure width of the path is denoted by d. Sometimes we denote it by w.
Then, the side of the inner square = (s – 2w)
Area of path = area of outer square – area of inner square = s.s – (s – 2w)(s – 2w)

If the path is laid outside and around a square of side ‘s’, then, the side of the outer square = (s + 2w)
Area of path = area of outer square – area of inner square = (s + 2w)(s + 2w) – s.s

Example:
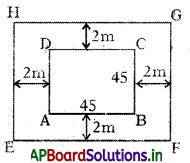
A square flowerbed is surrounded by a path 2 m wide around it. If the side of the flowerbed is 45 m, find the area of the path around the square flowerbed.
Answer:

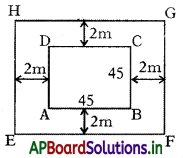
In the above figure,
EFGH is the outer boundary of the path.
Let each side of the flowerbed = 45 m
Then, the area of the square flowerbed ABCD = 452 m² = 2025

Now, the side of the square
EFGH = (45 + 2) m = 47 m
So, the area of square
EFGH = 472 m² = 2209
Therefore, area of the path = Area of EFGH – Area of ABCD
= 2209 – 2025
= 184 m²

→ Area of a circle is the region occupied by the circle in a two-dimensional plane.
It can be calculated using a formula, A = πr², (Pi r-squared) where r is the, radius of the circle. The unit of area is the square unit, such as m², cm², etc.
Area of Circle = πr² or πd²/4, (square unit) where π = 22/7 or 3.14

The circle is divided into equal sectors and the sectors are arranged as shown in the figure below. The area of the circle will be equal to that of the parallelogram-shaped figure formed by the sectors cut out from the circle. Since the sectors have equal area, each sector will have equal arc length. The red coloured sectors will contribute to half of the circumference and blue coloured sectors will contribute to the other half. If the number of sectors cut from the circle is increased, the parallelogram will eventually look like a rectangle with length equal to nr and breadth equal to r.

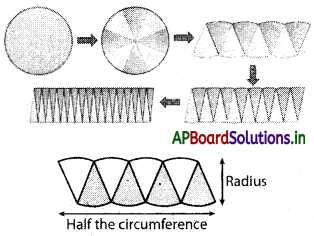
Now the area of the circle = Area of the parallelogram = πr . r = πr²

→ Area of pircular path or annulus: A circular path or an Annulus is a ring shaped object, bounded by the circumference of two concentric circles of two different radii. An Annulus is much like the throw-ring. One way to think of it is a circular disk with a circular hole . in it. The outer and inner circles that define the ring are concentric, that shares a common center point.

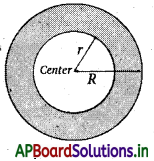
The dimensions of an annulus are defined by the outer radius R and the inner radius r, respectively. The area of a cir¬cular ring can be found by subtracting the area of a small circle from that of the area of the large circle.
Here are formulas to find Area of Annulus.
A = π(R² – r²)
Where,
A = Area of Annulus
R = Outer radius
r = Inner radius
(Pi)π = is approximately 3.142

Example:
Find the area of the path, where a path is 14 cm wide, surrounds a circular lawn whose diameter is 360 cm.
Answer:
Given,
Width of the path =14 cm
Diameter of the inner circle is 360 cm.

Radius of inner circle (r) = 360/2 = 180 cm
Radius of outer circle is (R) = 180 + 14 = 194 cm

A = π(R² – r²)
= 3.142(R + r)(R – r)
= 3.142 (194 + 180) (194 – 180)
= 3.142 × 374 ×14
= 16451.5 cm²