Students can go through AP Board 7th Class Maths Notes 12th Lesson Symmetry to understand and remember the concept easily.
AP Board 7th Class Maths Notes 12th Lesson Symmetry
→ If a line divide the given figure into two coincidental parts, then the figure is said to bd ‘symmetrical’ and the line is called the ‘axis of symmetry’ or ‘line of symmetry’.
→ A figure can have one or more than one lines of symmetry or axes of symmetry.
→ If we rotate a figure, about a fixed point by a certain angle and the figure looks exactly the same as before, we say that the figure has rotational symmetry.
→ The angle of turning during rotation is called the angle of rotation.
→ All figures have rotational symmetry of order 1, as can be rotated completely through 360° fo come back to their original position. So, we say that a figure has rotational symmetry only when the order of symmetry is more than 1.
→ Some shapes have only line symmetry and some have only rotational symmetry and some have both. Squares, equilateral triangles and circles have both line and rotational symmetry.
![]()
→ Each regular polygon has as many lines of symmetry’ as it’s sides.

→ Symmetry: Symmetry is defined as a proportionate and balanced similarity that is found in two halves of an object, that is, one-half is the mirror image of the other half. An object has symmetry’ it can be divided into two identical pieces.

→ Real-life examples of symmetry:
- Reflection of trees in clear water and reflection of mountains in a lake.
- Wings of most butterflies are identical on the left and right sides.
- Some human faces are the same on the left and right side.
- People can also have a symmetrical mustache.
→ In general usage, symmetry most often refers to mirror or reflective symmetry; that is a line (in 2-D) or plane (in 3-D) can be drawn through an object such that the two halves are mirror images of each other. An isosceles triangle and a human face are examples.
→ There are four types of symmetry that can be observed in various cases.
- Translational symmetry.
- Rotational symmetry.
- Reflexive symmetry.
- Glide symmetry.
→ Line of symmetry:
The imaginary axis or line along which you can fold a figure to obtain the symmetrical halves is called the line of symmetry.
→ A figure has a line of symmetry, if there is a line about which the figure may be folded so that the two parts of the figure will coincide. A figure has a line of symmetry, if there is a line about which the figure may be folded so that the two parts of the figure will coincide.
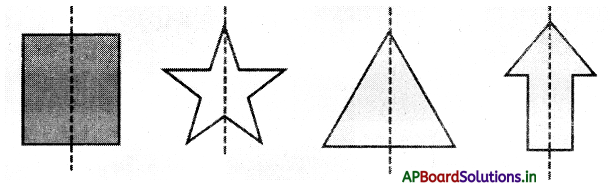
The line of symmetry can be categorized based on its orientation as:
- Vertical Line of Symmetry
- Horizontal Line of Symmetry
- Diagonal Line of Symmetry
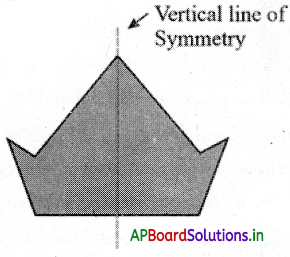
→ A vertical line of symmetry is that line that runs down vertically, divides an image into two identical halves. For example, the following shape can be split into two identical halves by a standing straight line. In such a case, the line of symmetry is vertical.
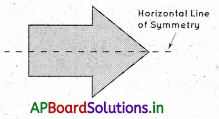
→ The horizontal line of symmetry divides a shape into identical halves, when split horizontally, i.e., cut from right to left or vice-versa. For example, the following shape can be split into two equal halves when cirt horizontally. In such a case, the line of symmetry is horizontal.
→ A diagonal line of symmetry divides a shape into identical halves when split across the diagonal corners. For example, we can split the following square shape across the corners to form two identical halves. In such a case, the line of symmetry is diagonal.

→ A line of symmetry is an axis along which an object when cut, will have identical halves. These objects might have one, two, or multiple lines of symmetry.
- One line of symmetry
- Two lines of symmetry
- Infinite lines of symmetry
→ One Line of Symmetry: Figures with one line of symmetry are symmetrical only about one axis. It may be horizontal, vertical, or diagonal. For example, the letter “A” has one line of symmetry, that is the vertical line of symmetry along its center.
→ Two Lines of Symmetry: Figures with two lines of symmetry are symmetrical only about two lines. The lines may vertical, horizontal, or diagonal lines. For example, the rectangle has two lines of symmetry, vertical and horizontal.
→ Infinite Lines of Symmetry: Figures with infinite lines of symmetry are symmetrical only about two lines. The lines may vertical, horizontal, or diagonal lines. For example, the rectangle has two lines of symmetry, vertical arid horizontal.
![]()
→ The following table shows the examples for different shapes with the number of lines of symmetry that they have.
| Number of lines of symmetry | Examples of figures |
| No line of symmetry | Scalene triangle |
| Exactly one line of symmetry | Isosceles triangle |
| Exactly two lines of symmetry | Rectangle . |
| Exactly three lines of symmetry | Equilateral triangle |
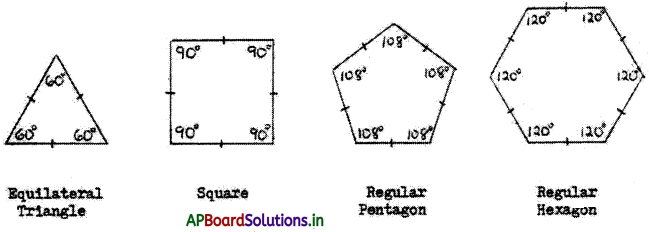
→ Regular Polygon:
If all the sides of a polygon or angles of a polygon are equal, then it is called a regular polygon.
Example: Equilateral triangle, square etc.
→ Rotational Symmetry: If a figure is rotated around a centre point and it still appears exactly as it did before the rotation, it is said to have rotational symmetry.
Example: Squares, circles, regular hexagon, etc. have rotational symmetry.
→ Center of Rotation: For a figure or object that has rotational symmetry, the fixed point around which the rotation occurs is called the centre of rotation.
Example: The centre of rotation of a table fan is the centre of the table fan from which its blades originate.
→ Angle of Rotational Symmetry: For a figure or object that has rotational symmetry, the angle of turning during rotation is called the angle of rotation.
Example: When a square is rotated by 90 degrees, it appears the same after rotation. So, the angle of rotation for a square is 90 degrees.
→ In the same way, a regular hexagon has an angle of symmetry as 60 degrees, a regular pentagon has 72 degrees and so on.
![]()
→ Order of Rotational Symmetry: The number of positions in which a figure can be rotated and still appears exactly as it did before the rotation, is called the order of symmetry. For example, a star can be rotated 5 times along its tip and look at the same every time. Hence, its order of symmetry is 5.

If we consider the order of symmetry for regular hexagon it is equal to 6, since it has 6 equal sides and is rotated with an angle of 60 degrees.
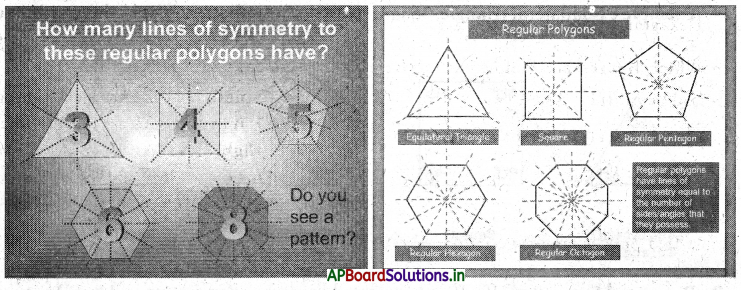
Number of lines of symmetry of a regular polygon is equal to number of sides in it.
→ Rotational Symmetry Letters: There are many capital letters of English alphabets which has symmetry when they are rotated clockwise or anticlockwise about an axis.
Example : Z, H, S, N and O. When these letters are rotated 180° clockwise or anticlockwise the letters appears to be same.