Students can go through AP Board 7th Class Maths Notes 1st Lesson Integers to understand and remember the concept easily.
AP Board 7th Class Maths Notes 1st Lesson Integers
→ Brahmagupta :
The idea of the products involving negative numbers was first considered by Brahmagupta of India in the seventh century AD. It is described in his book Brahmasphuta Siddantham. He makes the definition such as negative times negative is positive to give a single general method for formulizing problems involving a number and its square and for finding their solutions.
→ The collection of natural numbers (1, 2, 3, 4, 5 ) zero (0) and negative numbers (- 1, – 2, – 3, – 4, – 5, ) are integers.
- The product of two positive integers or two negative integers is positive integer.
- The product of one positive integer and one negative integer is negative integer.
- The quotient of two positive integers (or two negative integers) is positive integer.
- The quotient of one positive integer and one negative integer is negative integer.
- To simplify arithmetic expressions, we must follow the BODMAS rule (Brackets, Of, Division, Multiplication, Addition, Subtraction).
- The brackets in an expression have to be opened in the order of vinculum, simple brackets, curly brackets and square brackets, i.e., [{(-)}] to be opened from inside to outwards.
- Numerical value of an integer (without considering its sign) is the absolute value of that integer. Absolute value never be negative.
→ Natural numbers:
The counting numbers 1, 2, 3, …… are called natural numbers, denoted by N.
![]()
→ Whole numbers:
The collection of natural numbers (1, 2, 3, ….} together with {0} zero is called the collection of whole numbers, represented by W.
→ Integers:
The collection of natural numbers {1, 2, 3, {0} zero together with negative numbers (-1, – 2, -3, called the collection of integers, represented by I or Z.
For example : 1, – 1, 0, 101 and – 101.
→ They can be ordered by being placed on a number line, the number to the right is always greater than the one to the left.
→ We use integers in our daily life situations :
We use positive integers to measure weights, lengths, height and age etc.
- Weight of Latha is 32 kg
- John’s height is 145 cm
- Length of a pencil is 22 cm
- Teacher’s age is 32 years
→ We use positive integers to denote money deposited with a bank.
Raju deposited a sum of Rs. 8000 with a bank.
→ We use positive integers to measure the average rain fall of given regions.
Average rain fall of Guntur in December 2020 is mm.
→ We use negative integers to measure the depth below the sea level.
We use negative integers to denote the money borrowed.
Manisha borrowed a sum of Rs. 5000 from her friend.
We use negative integers to denote the temperatures below zero degrees Celsius.
Note: Zero is neither a positive integer nor a negative integer.
- Every positive integer is greater than zero,
i. e. 1, 2, 3, 4, …. are greater than zero. - Every negative integer is less than zero,
i. e.-1,-2,-3,-4, …. are lefes than zero.
→ Every integer can be expressed as a sum of any two integers in many ways.
Example :
-12 = 5 + (-17)
= (-6) + (-6)
= (-8) + (-4)
= 16 + (-28) …… etc.
→ Every integer can be expressed as a difference of any two integers in many ways.
Example :
-12 = (-17) – (-5)
= (-6) – (6)
= (-8) – (4)
= 16 – (28) etc.
→ Product of integers :
The product of two positive integers is always a positive integer.
Example :
9 × 4 = 36
3 × 7 = 21
6 × 9 = 54
13 × 7 = 91
→ Product of a positive integer and a negative integer is always a negative integer.
Example :
8 × (-5) = -40
14 × (-6) = -84
3 × (-7) = -21
6 × (-9) = -54
4 × (-1) = -4
→ Product of a negative integer and a positive integer is always a negative integer.
Example :
-7 × (5) = -35
-9 × (4) = -36
-13 × (7) = -91
-3 × (7) = -21
-8 × (1) = -8
![]()
→ Product of two negative integers is always a positive integer.
Example :
-9 × -4 = 36
-13 × -7 = 91
-3 × -7 = 21
-6 × -9 = 54
→ From these examples we can conclude that,
- If two integers have same signs, their product is positive.
- If two integers have opposite signs, then their product is negative.
→ For any two integers a and b
a × b = ab
-a × b = -ab
a × -b = -ab
-a × -b = ab
→ Division of integers :
- If a positive integer is divided by a positive integer, the quotient is positive.
Example : 18 ÷ 6 = 3 - If a negative integer is divided by a positive integer, the quotient is negative.
Example : -18 ÷ 6 = -3 - If a positive integer is divided by a negative integer, the quotient is negative.
Example : 18 + -6 = -3 - If a negative integer is divided by a negative integer, the quotient is positive.
Example : -18 + -6 = 3
From these examples we can conclude that,
- If two integers have the same signs, their quotient is positive.
- If two integers have opposite signs, then their quotient is negative.
- Symbols of belongs to and does not belong to e and g.
Example :
- 4 is a natural number. We denote it by 4 ∈ N.
- -4 is not a natural number. We denote it by 4 ∉ N.
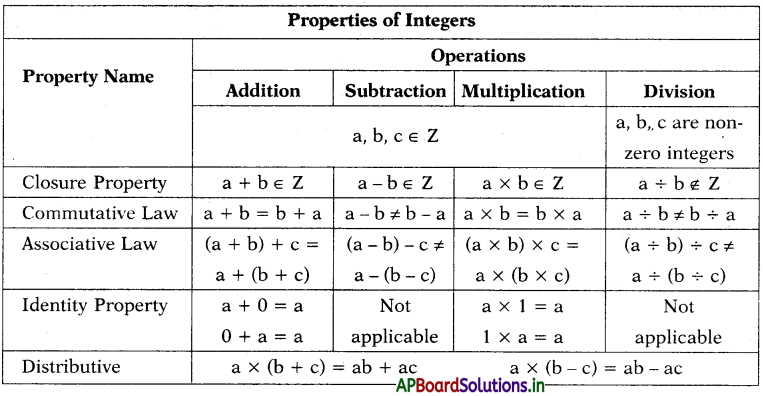
→ Properties of integers :
Closure property:
(i) For any two integers a and b, (a + b) is always an integer. In other words integers are closed with respect to addition.
Example:
5 + 3 = 8
-5 + 3 = -2
5 + (-3) = 2
-5 + (-3) = -8
(ii) For any two integers a and b, (a – b) is always an integer. In other words integers
are closed with respect to subtraction.
Example :
5 – 3 = 2
-5 – 3 = -8
5 – (-3) = 8
-5 – (-3) = -2
(iii) For any two integers a and b, (a × b) is always an integer. In other words integers are closed with respect to multiplication.
Example:
5 × 3 =15
-5 × 3 =-15
5 × (-3) = -15
-5 × (-3) =15
(iv) For any two integers a and b, (a + b) is always not an integer. In other words integers are not closed with respect to division.
Example:
15 + 3 = 5
-15 + 3 = -5
15 +(-3) = -5
-15 +(-3) = 5
But (5 + 3), (3 + 5), (-15 + 2) are not integers.
So we conclude that integers are not closed with respect to division.
Also for any integer a, (a+0) is not an integer.
→ Commutative law:
(i) For any two integers a and b, (a + b) is always equals to (b + a). In other words integers are commutative with respect to addition.
Example :
5 + 3 = 8 = 3 + 5
-5 + 3 = -2 = 3 + (-5)
5+ (-3) = 2 = (-3) + 5 and
-5 + (-3) = -8 = (-3) + (-5)
(ii) For any two integers a and b, (a × b) is always equals to (b × a). In other words integers are commutative with respect to multiplication.
Example :
5 × 3 = 15 = 3 × 5
-5 × 3 = -15 = 3 × (-5)
5 × (-3) = -15 = (-3) × 5 and
-5 × (-3) = 15 = (-3) × (-5)
(iii) For any two integers a and b, (a – b) is always not equals to (b – a). In other words integers are not commutative with respect to subtraction.
Example:
5 – 3 ≠ 3 – 5
(iv) For any two integers a and b, (a ÷ b) is always not equals to (b ÷ a). In other words integers are ftot commutative with respect to division. ‘
Example: 15 – 3 ≠ 3 – 5
![]()
→ Associative Law: For any three integers a, b and c we have
(a + b) + c is always equal to a + (b + c). In other words integers are associative with respect to addition.
(a + b) + c = a + (b+ c)
Example: (5 + 3) + 8 = 16 = 5 + (3 + 8)
Also, integers are associative with respect to multiplication.
(a × b) × c = a × (b × c)
Example: (5 × 3) × 2 = 30 = 5 × (3 × 2)
But integers are not associative with respect to subtraction.
(a – b) – c = a – (b – c)
Example: (5 – 3) – 2 ≠ 5 – (3 – 2)
Also integers are not associative with respect to division.
(a + b) + c = a + (b + c)
Example: (5 + 3) + 2 ≠ 5 + (3 + 2)
The division of integers by zero is not defined.
→ Additive identity :
For any integer ‘a’ we have
a + 0 = 0 + a = a
Here ‘0’ is called additive identity.
Example:
-5 + 0 = 0 + (-5) = -5
→ Multiplicative identity:
For any integer ‘a’ we have a × 1 = 1 × a = a
Here ‘1’ is called multiplicative identity.
Example:
8 × 1 = 1 × 8 = 8 .
-5 × 1 = 1 × (-5) = -5
For any integer a there exists an integer (-a) such that a + (-a) = 0 = (-a) + a.
Both integers a and – a are called additive inverse of each other.
Example :
7 + (-7) = 0 = (-7) + 7
-9 + 9 = 0 = 9 + (-9)
But the multiplicative inverse of an integer does not exist in the set of integers.
For any three integers a,b and c we have a × (b + c) = a × b + a × c
Example:
5 × (3 + 8) = 5 × 3 + 5 × 8
This is called distributive property of integers over addition.
Also a × (b – c) = a × b – a × c
This is called distributive property of integers over subtraction.
→ The product of n- positive integers is always a positive integer.
Example: 5 × 3 × 7 × 11 is a positive integer.
The product of n- number of negative integers is always a positive integer if ‘n’ is an even number.
Example:
-2 ×-2 = 4
-3 ×-3 × -3 × -3 = 81
-3 × -5 × -4 × -1 = 60
→ The product of ‘n’ number of negative integers is always a negative integer if ‘n’ is an odd number.
Example:
-2 × -2 × -2=-8
-3 × -5 × -4 × -1 ×-2 = -120
→ V BODMAS Rule:
The hierarchy of arithmetic operations in which they have to be carried out is given by a rule called V BODMAS rule.
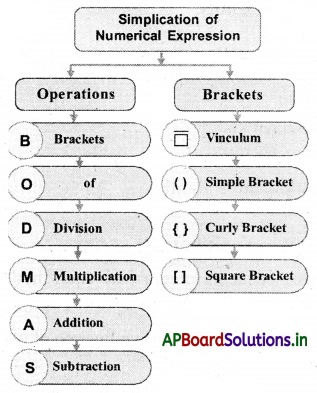
Brackets are symbols used in pairs to group things together.
Types of brackets include : Parentheses or “round brackets ( )” “square brackets” or “box brackets [ ]”, braces or “curly brackets { }”, “angle brackets < >”.
| Symbol | Name |
| – | vinculum or bar |
| ( ) | parentheses as small brackets |
| { } | Braces or curly brackets |
| [] | square brackets |
Example:
15 of 6 – [18 -.{14 – (3 + 2)}]
- Applying First the bracket rule
= 15 of 6 – [18 – {14 – 5}] - Applying Again the bracket rule
= 15 of 6 – [18 – 9] - Applying Again the bracket rule
= 15 of 6 – 9 - Now Multiplication comes before Subtraction
= 90 – 9 = 81
→ The absolute value of an integer :
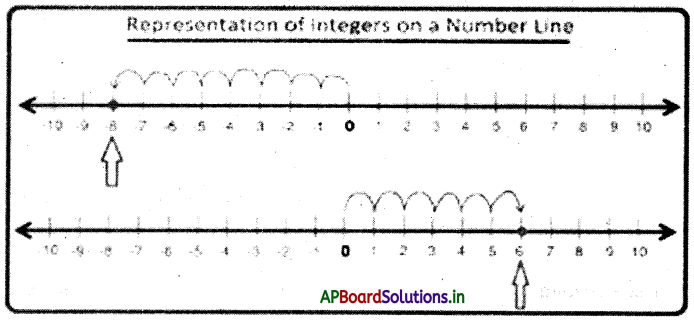
The absolute value of -8 can be understood as the distance of -8 from the zero ‘0’ on the number line”.
Hence the absolute value of -8 is 8 units.
Similarly absolute value of -9 = 9
Absolute value of -12 = 12
The absolute value of 6 can be understood as the distance of 6 from the zero ‘0’ on the number line”.
Hence the absolute value of 6 is 5 units.
Similarly absolute value of 11 – 11
Absolute value of 2 = 2
So the absolute value of an integer is the numerical value without its sign. It is denoted by | |.
|-5| = 5
|-7| = 7
|9| = 9
![]()
→ Number series :
A collection of numbers in which all numbers except the first number are formed by a simple rule.

→ Addition series : Each number is formed by adding a specific/fixed number to its previous number.
2, 5, 8, 11, 14, ………….
→ Fibonacci series : Every third number can be the sum of its preceeding two numbers.
3, 5, 8, 13, …………