SCERT AP 10th Class Maths Textbook Solutions Chapter 8 సరూప త్రిభుజాలు Exercise 8.3 Textbook Exercise Questions and Answers.
AP State Syllabus 10th Class Maths Solutions 8th Lesson సరూప త్రిభుజాలు Exercise 8.3
ప్రశ్న 1.
ఒక లంబకోణ త్రిభుజము మూడు భుజాలపై సమబాహు త్రిభుజాలు గీయబడ్డాయి. కర్ణము మీద గీసిన త్రిభుజ వైశాల్యము మిగిలిన రెండు భుజాల మీద గీసిన త్రిభుజాల వైశాల్యాల మొత్తమునకు సమానమని చూపండి.
సాధన.
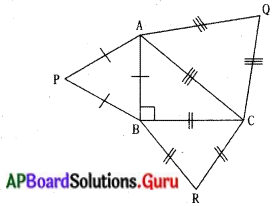
దత్తాంశము :
∆ABC లంబకోణ త్రిభుజం
∠B = 90°.
∆ABP, ∆AQC, ∆BCRల సమబాహు త్రిభుజాలు.
సారాంశము :
∆AQC వైశాల్యం = ∆APB వైశాల్యం + ∆BCR వైశాల్యం
నిరూపణ :
∆ABP ~ ∆BCR ~ ∆ACR (∵ సమబాహు త్రిభుజాలు ఎల్లప్పుడు సరూపాలు)
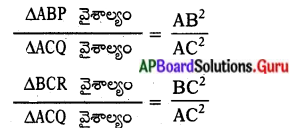
(∵ సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాని అనురూప భుజాల వర్గాల నిష్పత్తికి సమానం)
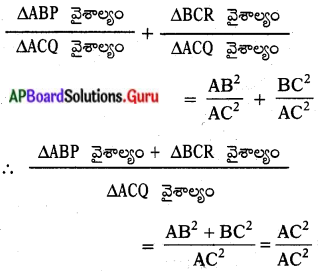
 (పైథాగరస్ సిద్ధాంతం నుండి)
(పైథాగరస్ సిద్ధాంతం నుండి)
∴ ∆ACQ వైశాల్యం = ∆ ABP వైశాల్యం + ∆ BCR వైశాల్యం.
![]()
ప్రశ్న 2.
ఒక చతురస్రము భుజముపై గీచిన సమబాహు త్రిభుజ వైశాల్యము, ఆ చతురస్ర కర్ణముపై గీచిన సమబాహు త్రిభుజ వైశాల్యములో సగము వుంటుందని చూపండి.
సాధన.
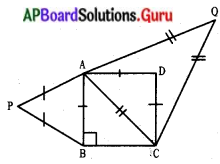
దత్తాంశము :
ABCD ఒక చతురస్రము ∆ABP మరియు ACQలు వరుసగా చతురస్ర భుజం, కర్ణాల మీద గీచిన సమబాహు త్రిభుజాలు.
సారాంశము :
∆ABP వైశాల్యం = \(\frac{1}{2}\) ∆ACQ వైశాల్యం
నిరూపణ :
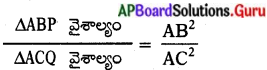 [∵ ∆ABP ~ ∆ACQ]
[∵ ∆ABP ~ ∆ACQ]
(∵ సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాని అనురూప భుజాల వర్గాల నిష్పత్తికి సమానం)
= \(\frac{\mathrm{AB}^{2}}{(\sqrt{2} \mathrm{AB})^{2}}\) [ABCD చతుర్భుజంలో]
= \(\frac{A B^{2}}{2 A B^{2}}=\frac{1}{2}\) [AC = √2 AB]
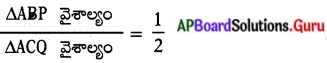
∴ ∆ABP వైశాల్యం = \(\frac{1}{2}\) ∆ACQ వైశాల్యం.
![]()
ప్రశ్న 3.
∆ ABCలో BC, CA, AB భుజాల మధ్య బిందువులు వరుసగా D, E, F. అయిన ∆DER మరియు ∆ABC ల వైశాల్యాల నిష్పత్తిని కనుగొనండి.
సాధన.
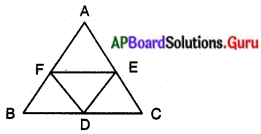
దత్తాంశము :
∆ABCలో; D, E మరియు , F లు BC, CA మరియు AB భుజాల మధ్య బిందువులు. ∆ABCలో AB, ACల మధ్య బిందువులను కలుపగా EF ఏర్పడినది.
FE || BC కావున \(\frac{A F}{F B}=\frac{A E}{E C}\)
(ప్రాథమిక అనుపాత సిద్ధాంత విపర్యయము నుండి)
అదే విధముగా AC మరియు BC లను DE ఒకే నిష్పత్తిలో విభజిస్తుంది. కావున DE || AB.
□BDEFలో ఎదుటి భుజాలు సమాంతరాలు (BD || EF మరియు DE || BF)
కావున OBDEF ఒక సమాంతర చతుర్భుజము ఇక్కడ DF ఒక కర్ణము.
∴ ∆BDF = ∆DEF ………… (1)
అదే విధముగా ∆DEF = ∆CDE అని నిరూపించవచ్చును. ………… (2) [∵ CDEF ఒక సమాంతర చతుర్భుజం] మరియు
∆DEF = ∆AEF …………. (3) [∵ □AEDF ఒక సమాంతర చతుర్భుజం]
(1), (2) మరియు (3) ల నుండి
∆AEF ≈ ∆DEF ≈ ∆BDF ≈ ∆CDE
అదే విధముగా ,
∆ABC = ∆AEF + ∆DEF + ∆BDF + ∆CDE = 4. ∆DEF
∆ABC : ∆DEF = 4 : 1.
![]()
ప్రశ్న 4.
∆ABCలో, XY || AC మరియు XYఆ త్రిభుజాన్ని రెండు సమాన వైశాల్యాలు గల భాగాలుగా AX విభజించును. అయిన \(\frac{\mathrm{AX}}{\mathrm{XB}}\) నిష్పత్తిని కనుగొనండి.
సాధన.
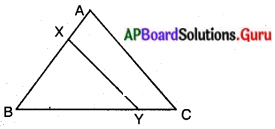
దత్తాంశము :
∆ABC లో XY | | AC.
సారాంశము :
\(\frac{\mathrm{AX}}{\mathrm{XB}}\) నిష్పత్తి , XY, ∆ABC ను సమాన వైశాల్యాలు గల భాగాలుగా విభజించును. ∆ABC, ∆XBY లలో ∠B = ∠B
∠A = ∠X [∵ XY || AC; ∠A, ∠X మరియు ∠C, ∠Yలు ఆసన్నకోణాల జత]
∆ABC ~ ∆XBY (కో.కో.కో సరూపకత ధర్మము ప్రకారము)
ఆ విధముగా \(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{XBY}}=\frac{\mathrm{AB}^{2}}{\mathrm{XB}^{2}}\)
[∵ రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల నిష్పత్తి వర్గమునకు సమానము)
\(\frac{2}{1}=\frac{\mathrm{AB}^{2}}{\mathrm{XB}^{2}}\)
[దత్తాంశంలో ∆BXY = ∆BAC కావున ∴ ∆ABC = 2 . ∆XBY]
2 = \(\left(\frac{\mathrm{AB}}{\mathrm{XB}}\right)^{2}\)
2 = \(\left(\frac{\mathrm{AX}+\mathrm{XB}}{\mathrm{XB}}\right)^{2}\)
2 = \(\left(\frac{\mathrm{AX}}{\mathrm{XB}}+\frac{\mathrm{XB}}{\mathrm{XB}^{\prime}}\right)^{2}\)
2 = \(\left(\frac{\mathrm{AX}}{\mathrm{XB}}+1\right)^{2}\)
⇒ \(\frac{\mathrm{AX}}{\mathrm{XB}}\) + 1 = √2
⇒ \(\frac{\mathrm{AX}}{\mathrm{XB}}\) = √2 – 1
కావున ఆ నిష్పత్తి \(\frac{\mathrm{AX}}{\mathrm{XB}}=\frac{\sqrt{2}-1}{1}\).
![]()
ప్రశ్న 5.
రెండు సరూపత్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి – అనురూప మధ్యగతాల నిష్పత్తి వర్గానికి సమానమని చూపండి.
సాధన.
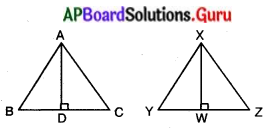
దత్తాంశము : ∆ABC ~ ∆XYZ
సారాంశము : \(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{XYZ}}=\frac{\mathrm{AD}^{2}}{\mathrm{XW}^{2}}\)
ఉపపత్తి : రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల నిష్పత్తి వర్గమునకు సమానము.
\(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{XYZ}}=\frac{\mathrm{AD}^{2}}{\mathrm{XW}^{2}}\) …………..(1) [∵ ∆ABC ~ ∆XYZ]
∆ABD మరియు ∆XYW లలో ∠B = ∠Y; ∠D = ∠W = 90°
(కో.కో.కో ఉప సిద్ధాంతము నుండి),
∆ABD ~ ∆XYW
∴ \(\frac{\Delta \mathrm{ABD}}{\Delta \mathrm{XYW}}=\frac{\mathrm{AB}^{2}}{\mathrm{XY}^{2}}=\frac{\mathrm{AD}^{2}}{\mathrm{XW}^{2}}\) …………..(2)
(1) మరియు (2) ల నుండి,
\(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{XYZ}}=\frac{\mathrm{AD}^{2}}{\mathrm{XW}^{2}}\)
ఆ విధముగా రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల నిష్పత్తి వర్గమునకు సమానము.
![]()
ప్రశ్న 6.
∆ABC ~ ∆DEF. BC = 3 సెం.మీ, EF = 4 సెం.మీ, ∆ABC వైశాల్యము = 54 చ.సెం.మీ అయిన ∆DEF వైశాల్యమును కనుగొనుము.
సాధన.
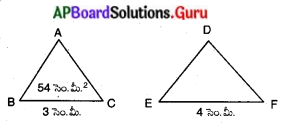
దత్తాంశము ప్రకారం, ∆ABC ~ ∆DEF.
BC = 3 సెం.మీ.; EF = 4 సెం.మీ. ∆ABC = 54 చ.సెం.మీ
∴ ∆ABC ~ DEF, కావున \(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{DEF}}=\frac{\mathrm{BC}^{2}}{\mathrm{EF}^{2}}\)
[∵ సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి. వాటి అనురూప భుజాల వర్గ నిష్పత్తికి సమానము].
\(\frac{54}{\Delta \mathrm{DEF}}=\frac{3^{2}}{4^{2}}\)
∴ ∆DEF = \(\frac{54 \times 16}{9}\) = 96 సెం.మీ.
![]()
ప్రశ్న 7.
త్రిభుజము ABCలో AB భుజాన్ని P వద్ద, AC ని Q వద్ద తాకునట్లు PQ ఒక సరళరేఖ, ఇంకా AP = 1 సెం.మీ., BP = 3 సెం.మీ. AQ = 1.5 సెం.మీ., CQ = 4.5 సెం.మీ. అయిన ∆APQ వైశాల్యము = \(\frac{1}{16}\) (∆ABC వైశాల్యము) అని చూపండి.
సాధన.
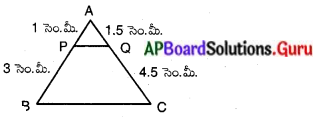
దత్తాంశము ప్రకారం, ∆ABC మరియు \(\overline{\mathrm{PQ}}\), AB ను P వద్ద మరియు AC ను Q వద్ద ఖండించుచున్నది.
AP = 1 సెం.మీ; AQ = 1.5 సెం.మీ BP = 3 సెం.మీ; CQ = 4.5 సెం.మీ
\(\frac{\mathrm{AP}}{\mathrm{BP}}=\frac{1}{3}\) ……………. (1);
\(\frac{\mathrm{AQ}}{\mathrm{QC}}=\frac{1.5}{4.5}=\frac{1}{3}\) ……………(2)
(1) మరియు (2) ల నుండి \(\frac{\mathrm{AP}}{\mathrm{BP}}=\frac{\mathrm{AQ}}{\mathrm{CQ}}\)
[∵ PQ, AB మరియు AC లను ఒకే నిష్పత్తిలో విభజించింది]
ప్రాథమిక అనుపాత సిద్దాంత విపర్యయము నుండి PQ || BC.
∆APQ మరియు ∆ABC లలో
∠A = ∠A (ఉమ్మడి కోణం)
∠P = ∠B [∵ PQ || BC సమాంతరరేఖల అనురూప కోణాలు] .
∠Q = ∠C
∴ ∆APQ ~ ∆ABC [∵ కో.కో.కో సరూప నియమము నుండి]
\(\frac{\Delta \mathrm{APQ}}{\Delta \mathrm{ABC}}=\frac{\mathrm{AP}^{2}}{\mathrm{AB}^{2}}\)
[∵సరూప త్రిభుజాల వైశాల్యాల ‘నిష్పత్తి వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము].
= \(\frac{1^{2}}{(3+1)^{2}}=\frac{1}{16}\)
∴ ∆APQ = \(\frac{1}{16}\) (∆ABC) నిరూపించబడినది.
![]()
ప్రశ్న 8.
రెండు సరూప త్రిభుజాల వైశాల్యాలు 81 చ.సెం.మీ మరియు 49 చ.సెం.మీ. పెద్ద త్రిభుజములో గీసిన లంబము పొడవు 4.5 సెం.మీ అయిన చిన్న త్రిభుజములో దాని అనురూప లంబము పొడవును కనుగొనండి. .
సాధన.
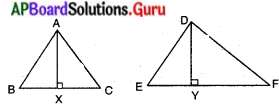
దత్తాంశము : ∆ABC ~ ∆DEF ∆ABC = 81 సెం.మీ2; ∆DEF = 49 సెం.మీ2; AX = 4.5 సెం.మీ
సారాంశము : DY పొడవు
ఉపపత్తి : \(\frac{\Delta \mathrm{ABC}}{\Delta \mathrm{DEF}}=\frac{\mathrm{AX}^{2}}{\mathrm{DY}^{2}}\)
[∵ రెండు సరూప త్రిభుజాల వైశాల్యాల నిష్పత్తి వాటి అనురూప భుజాల వర్గాల నిష్పత్తికి సమానము]
\(\frac{81}{49}=\frac{(4.5)^{2}}{D Y^{2}}\)
⇒ \(\left(\frac{9}{7}\right)^{2}=\left(\frac{4.5}{D Y}\right)^{2}\)
⇒ \(\frac{9}{7}=\frac{4.5}{\mathrm{DY}}\)
⇒ DY = 4.5 × \(\frac{7}{9}\)
∴ DY = \(\frac{7}{2}\) = 3.5 సెం.మీ.