Students can go through AP Board 7th Class Maths Notes 2nd Lesson Fractions, Decimals and Rational Numbers to understand and remember the concept easily.
AP Board 7th Class Maths Notes 2nd Lesson Fractions, Decimals and Rational Numbers
→ John Napier (1550-1617)
John Napier of Merchiston (UK) was born in the year 1550. He started his formal education at the age of 13 as was the common tradition of that time. However he soon dropped out of school and travelled to Europe. He returned to Scotland at the age of 21.
John Napier is founder of logarithms and he became so after spending long hours, doing lengthy calculations of astronomy. He also invented the so-called ‘Napier’s strips’ which were devices that could be used as calculators.
Napier also made improvements to the idea of the decimal fraction by starting the use of decimal point, a practice that very soon became common throughout Britain. Napier was widely recognised for his work in mathematics and astronomy. He died in the year 1617.
→ To add or subtract fractions they must have same denominator (like fractions).
→ For multiplication of fractions, we simply multiply numerators and multiply denominators.
→ To divide one fraction by another fraction, we have to multiply one fraction with the reciprocal of the another fraction.
→ To multiply decimal numbers by 10, 100, 1000, shift the decimal point in the product as many places to the right as number of zeroes after 1.
→ The number of decimal digits in the product of any two decimal numbers is equal to the sum of decimal digits that are multiplied.
![]()
→ While dividing a decimal number by 10, 100 or 1000, the digits of the number and the quotient are same but the decimal point in the quotient shifts to the left by as many places as there are zeros 1 after.
Fraction: Apart of a whole is known as a fraction.
Example: \(\frac{3}{4}, \frac{5}{8}\)
1/8 Fraction:

Fraction of a whole number: To find the fraction of a whole number we multiply the fraction with the whole number.
Example: \(\frac{3}{4}\) of 36 = \(\frac{3}{4}\) × 36 = 3 × 9 = 27
→ Total number of students in a class is 48. On a particular day only \(\frac{5}{8}\) of the students are present. Find the number of students present in the class.
Answer:
Number of students present in the class = \(\frac{5}{8}\) of 48 = \(\frac{5}{8}\) × 48 = 5 × 6 = 30
→ Fraction of a fraction: To find the fraction of a fractional number we multiply the first fraction with the second fraction.
Example: \(\frac{3}{4}\) of \(\frac{5}{8}\) = \(\frac{3}{4} \times \frac{5}{8}=\frac{15}{32}\)
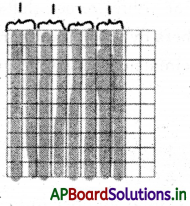
→ Decimal fractions: Fractions with denominators 10, 100, 1000, 10000, ………….. etc. are called decimal numbers or decimal fractions.
Example: \(\frac{1}{10}, \frac{1}{100}, \frac{1}{1000}\) are decimal fractions.
Example:
Note: The fraction \(\frac{1}{10}, \frac{1}{100}, \frac{1}{1000}\),………… can be written as 0.1, 0.01, 0.001,… and read as
- Zero point one
- Zero point zero one
- Zero point zero zero one.
![]()
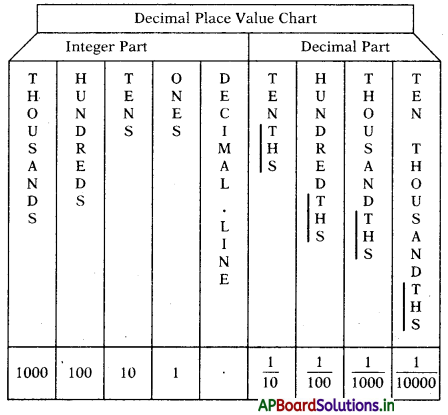
→ Expanded form of decimal numbers:

→ Addition and subtraction of decimal numbers:
- Step-1: Decimal numbers are written one below the other with the decimal points lined up in the same column.
- Step-2: Add or subtract as we would do in the case of whole numbers.
- Step-3: Place the decimal in the result in line with the other decimal points.
For example: 56.39 + 18.61

→ Multiplication of decimals with whole numbers:
Method – 1:
Convert the decimal into a fraction and then multiply. Finally convert the fraction into decimal.
Example: 4 × 2.3 = 4 × \(\frac{23}{10}=\frac{92}{10}\) = 9.2
Method – 2:
Multiply the whole numbers ignoring the decimals.
4 × 2.3 = 92
Now place the decimal point in the product according to the number of decimal places in the given decimal. Here only one decimal place is the given number.
4 × 2.3 – 9.2
Method-3:
4 × 2.3 = 2.3 + 2.3 + 2.3 + 2.3 = 9.2
We can find the product by repeated addition also.
Multiplication of decimal by 10, 100, 1000, ….
To multiply decimal numbers by 10, 100, 1000,… etc., just shift the decimal point in the given decimal as many places to the right, as there are zeroes in the multiplier.
Example:
- 236.568 × 10 = 2365.68 (one zero, shift decimal to one place to the right side)
- 236.568 × 100 = 23656.8 (two zeroes, shift decimal to two places to the right side)
- 236.568 × 1000 = 236568.0 (three zeroes, shift decimal to three places to the right side)
→ Multiplication of two decimals:
Multiplying decimals is the same as multiplying whole numbers except for the placement of the decimal point in the answer. When you multiply decimals, the decimal point is placed in the product so that the number of decimal places in the product is the sum of the decimal places in the factors.
- Step-1: multiply the given numbers ignoring the decimals.
- Step-2: the decimal point is placed in the product so that the number of decimal places in the product is the sum of the decimal places in the factors.
Example: 2.3 × 4.5 = 23 × 45 = 1035
Answer:
10.35
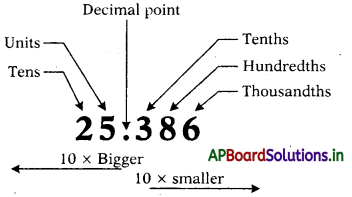
Note: The number of decimal places in the product of any two decimal numbers is equal to the sum of decimal digits that are multiplied.
![]()
→ Division of decimal numbers:
While dividing decimal numbers by 10, 100, 1000 or the digits of the number and the digits of quotient are same, but the decimal point in the quotient shifts to the leftby as many places as there are zeroes in the divisor (after 1).
Example: ‘
- 236.568 ÷ 10 = 23.6568 (one zero, shift decimal to one place to the left side)
- 236.568 ÷ 100 = 2.36568 (two zeroes, shift decimal to two places to the left side)
- 236.568 ÷ 1000 = 0.236568 (three zeroes, shift decimal to three places to the left side)
→ Division of decimal numbers by whole numbers:
Method-1: Convert the decimal number into fraction and then carry out simplifications as in the case of fractions.
Example: 3.6 ÷ 4
3.6 ÷ 4 = \(\frac{36}{10} \div \frac{4}{1}=\frac{36}{10} \times \frac{1}{4}=\frac{9}{10}\) = 0.9
Method-2: Convert the decimal number in to a whole number and then carry out simplifications as in the case of fractions.
- Divide the whole number by the divisor.
- Then mark the decimal point to the quotient from right mode to left according to the number of decimal places in the given decimal.
Example: 3.6 ÷ 4
3.6 ÷ 4 = 36 ÷ 4 = 9 and the final answer is 0.9.
Method-3: Pictorial representation
Use Models to Divide Decimals by Whole Numbers
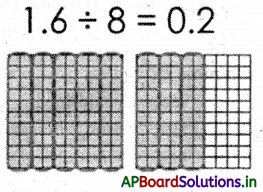
![]()
→ Division of decimal numbers by decimal number:
Method-1: Convert the decimals into equivalent fractions and then carryout simplifications as in the case of fractions.
Example: 1.5 ÷ 0.3
1.5 ÷ 0.3 = \(\frac{15}{10} \div \frac{3}{10}=\frac{15}{10} \times \frac{10}{3}=\frac{15}{3}\) = 5
Method-2: Convert the decimal numbers into equivalent whole numbers and then carryout simplifications as in the case of whole numbers.
Example: 1.5 ÷ 0.3
1.5 ÷ 0.3 = (1.5 × 10) ÷ (0.3 × 10)
= 15 ÷ 3 = 5
Method-3: Pictorial representation
Example: 0.8 ÷ 0.2
0.8 ÷ 0.2 = 4