Students can go through AP Board 7th Class Maths Notes 5th Lesson త్రిభుజాలు to understand and remember the concept easily.
AP Board 7th Class Maths Notes 5th Lesson త్రిభుజాలు
→ మూడు సరళ రేఖలచే ఏర్పడిన సరళ సంవృత సమతల పటమును త్రిభుజం అంటారు.
→ భుజముల ఆధారంగా, త్రిభుజములు మూడు రకములు. అవి :
- సమబాహు త్రిభుజం,
- సమద్విబాహు త్రిభుజం,
- విషమబాహు త్రిభుజం.
→ కోణములు ఆధారంగా త్రిభుజములు మూడు రకములు. అవి :
- అల్పకోణ త్రిభుజం,
- అధికకోణ త్రిభుజం,
- లంబకోణ త్రిభుజం.
→ త్రిభుజములో అంతర కోణముల మొత్తము 180°.
→ ఒక త్రిభుజంలో బాహ్యకోణం, దాని అంతరాభిముఖ కోణముల మొత్తమునకు సమానము.
![]()
→ త్రిభుజములో భుజముల కొలతల ధర్మాలు :
- ఒక త్రిభుజంలో ఏవైనా రెండు భుజముల మొత్తము, మూడవ భుజం కన్నా ఎక్కువ.
- ఒక త్రిభుజములో ఏ రెండు భుజముల భేదమైన మూడవ భుజం కన్నా తక్కువ.
→ త్రిభుజము : మూడు రేఖా ఖండాలతో ఏర్పడిన సరళ సంవృత పటాన్ని త్రిభుజము అంటారు.
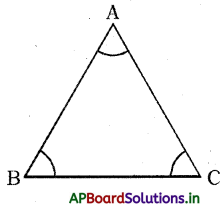
త్రిభుజంలోని భాగాలు : మూడు శీర్షాలు, మూడు కోణాలు, మూడు భుజాలు.
త్రిభుజం ABC లో (AABCలో)
మూడు శీర్షాలు : A, B మరియు C
మూడు కోణాలు : A, B మరియు ∠C (లేదా) ∠BAC, ∠ABC మరియు ∠BCA
మూడు భుజములు : \(\overline{\mathrm{AB}}, \overline{\mathrm{BC}}\) మరియు \(\overline{\mathrm{CA}}\)
→ త్రిభుజాల వర్గీకరణ : త్రిభుజాలను
- భుజాల కొలతను బట్టి,
- కోణాలను బట్టి రెండు విధాలుగా విభజిస్తారు.
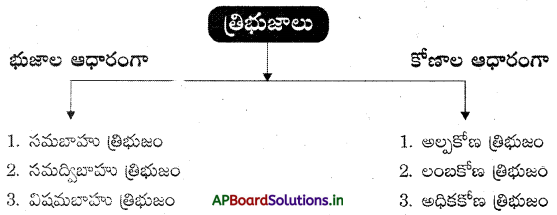
→ భుజాల కొలతల ఆధారంగా, త్రిభుజాలను మూడు రకాలుగా వర్గీకరించవచ్చు. అవి :
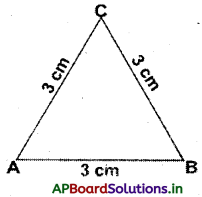
1. సమబాహు త్రిభుజం : అన్ని భుజాలు సమానంగా ఉన్న త్రిభుజమును సమబాహు త్రిభుజం అంటారు.
ఉదా :
(i) ∆ARC లో.
AB = BC = CA = 3 సెం.మీ.
(ii) ∆PQRలో PQ = QR = RP
2. సమద్విబాహు త్రిభుజం : రెండు భుజాలు సమానంగా ఉన్న త్రిభుజమును సమద్విబాహు త్రిభుజం అంటారు.
ఉదా :
(i) ∆KLM లో KM = ML = 2.5 సెం.మీ.
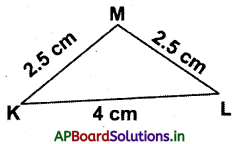
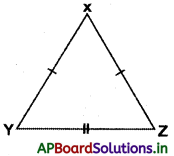
(ii) ∆XYZ లో,
XY = XZ
→ విషమబాహు త్రిభుజం : ఏ రెండు భుజాలు సమానంగా లేని త్రిభుజమును విషమబాహు త్రిభుజము అంటారు.
ఉదా :
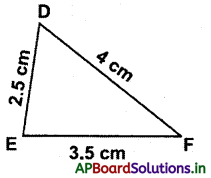
(i) ∆DEF లో
DE ≠ EF ≠ FD
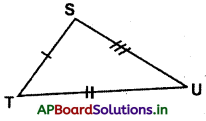
(ii) ∆STU లో
ST ≠ TU ≠ US
→ కోణాల కొలతల ఆధారంగా త్రిభుజాలను మూడు రకాలుగా వర్గీకరించవచ్చును. అవి :
1. అల్పకోణ త్రిభుజం : త్రిభుజము యొక్క అన్ని కోణాలు అల్పకోణములుగా గల త్రిభుజమును అల్పకోణ త్రిభుజం అంటారు. ఉదా :
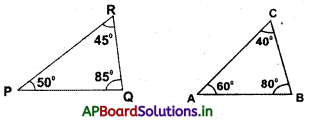
2. లంబకోణ త్రిభుజం : త్రిభుజములో ఒక కోణం లంబకోణం గల త్రిభుజమును లంబకోణ త్రిభుజం అంటారు.
ఉదా
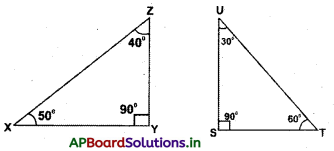
3. అధికకోణ త్రిభుజం : త్రిభుజములో ఒక కోణం అధిక కోణంగా గల త్రిభుజమును అధిక కోణ త్రిభుజం అంటారు.
ఉదా :
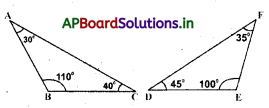
![]()
→ త్రిభుజ అంతరకోణాల మొత్తము-ధర్మము : త్రిభుజం లోని మూడు అంతర కోణాల మొత్తం 180°.
∆ABC లో ∠A + ∠B + ∠C = 180°.

ఒక లంబకోణ త్రిభుజంలో లంబకోణేతర కోణాలు రెండూ అల్పకోణాలు మరియు ఆ రెండు కోణాలు పూరకాలు. అనగా ఆ రెండు కోణాల మొత్తము 90°. ∆ABC లో, ∠B = 90°. కనుక ∆ABC ఒక లంబకోణ త్రిభుజము.
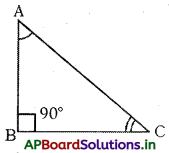
∆ABC లో ∠A + ∠C = 90°.
→ త్రిభుజ బాహ్యకోణ ధర్మము : ఒక త్రిభుజంలోని బాహ్య కోణము, దాని యొక్క అంతరాభిముఖ కోణాల మొత్తమునకు సమానము.
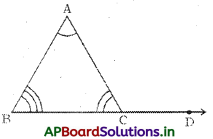
∆ABC లో ∠ACD = ∠A + ∠B
→ త్రిభుజము యొక్క భుజాల అసమానత్వ ధర్మాలు :
i) ఒక త్రిభుజంలోని ఏవైనా రెండు భుజాల మొత్తం మూడవ భుజం కన్నా ఎక్కువ.
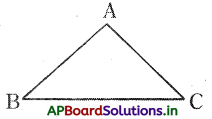
∆ABC లో,
- AB + AC > BC
- BC + AC > AB
- AB + BC > AC
(ii) ఒక త్రిభుజంలోని ఏ రెండు భుజాల భేదము, మూడవ భుజం కన్నా తక్కువ.
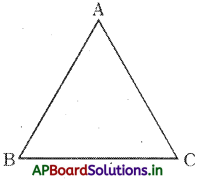
- AB – BC < AC
- BC – AC < AB
- AC – AB < BC
![]()
→ త్రిభుజ భుజాలకు మరియు కోణాలకు మధ్య గల సంబంధము :
(i) ఏ త్రిభుజంలో అయిన అతి చిన్న కోణమునకు ఎదురుగా ఉన్న భుజము, మిగిలిన రెండు భుజాల కన్నా చిన్నది. అలాగే
(ii) ఏ త్రిభుజంలో అయిన అతి పెద్ద కోణమునకు ఎదురుగా గల భుజము మిగిలిన రెండు భుజాల కన్నా పెద్దది.
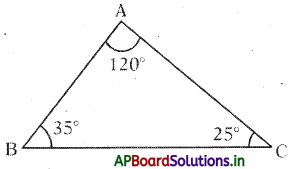
∆ABC లో, ∠A = 120°, ∠B = 35°, ∠C = 25°
∠C కోణము అతి చిన్నది. కావున ∠C కి ఎదురుగా గల భుజము BC మిగిలిన AC, AB కన్నా చిన్నదిగా ఉంటుంది.
∠C < ∠B కావున \(\overline{\mathrm{AB}}<\overline{\mathrm{AC}}\) మరియు
∠C < ∠A కావున \(\overline{\mathrm{AB}}<\overline{\mathrm{BC}}\) అలాగే ∠A కోణము అతి పెద్ద కోణము. కావున ∠A కు ఎదురుగా గల భుజం \(\overline{\mathrm{BC}}\) మిగిలిన రెండు భుజాల కన్నా పెద్దది. ∠A > ∠B కావున \(\overline{\mathrm{BC}}<\overline{\mathrm{AC}}\) మరియు ∠A > ∠C కావున \(\overline{\mathrm{BC}}<\overline{\mathrm{AB}}\).
→ లంబకోణ త్రిభుజంలో లంబకోణము (90°) మిగిలిన కోణాల కన్నా పెద్దది. కావున 90° గా గల కర్ణము. మిగిలిన రెండు భుజాల కన్నా పెద్దది.
∆ABC లో,
∠B = 90° కావున ∠B కి ఎదురుగా గల భుజం AC (కర్ణము) అతి పెద్ద భుజము అవుతుంది.
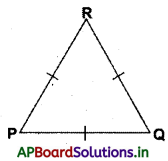
(iii) ఒక త్రిభుజంలో సమాన కోణాలకు ఎదురుగా గల భుజాలు సమానము. అలాగే సమాన భుజాలకు ఎదురుగా గల కోణాలు సమానము.
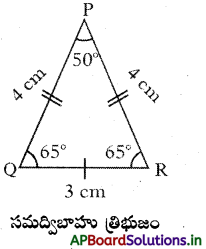
3 cm సమద్విబాహు త్రిభుజం సమద్విబాహు త్రిభుజంలో, PQ = PR కావున ∠R = ∠Q అలాగే ∠Q = ∠R కావున PQ = PR అవుతుంది.
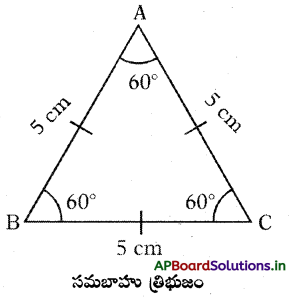
సమబాహు త్రిభుజం సమబాహు త్రిభుజంలో ప్రతికోణము సమానము. అనగా ప్రతికోణము .60. ∠A = ∠B = ∠C = 60° మరియు BC = AC = AB