Students can go through AP Board 7th Class Maths Notes 4th Lesson రేఖలు మరియు కోణాలు to understand and remember the concept easily.
AP Board 7th Class Maths Notes 4th Lesson రేఖలు మరియు కోణాలు
→ యూక్లిడ్ (323 – 283 BC) ఒక .గ్రీకు గణిత శాస్త్రవేత్త. ఆయన “రేఖాగణిత పితామహుడు”గా ప్రసిద్ధి చెందాడు. ఆయన “ఎలిమెంట్స్” అనే పేరుతో ఒక పుస్తకాన్ని రచించెను. ఇది రేఖాగణితాన్ని గురించి వివరించే 13 పుస్తకాల సమాహారం. గణిత శాస్త్ర చరిత్రలో “ఎలిమెంట్స్” అత్యంత ప్రభావితమైన రచన. ఆయన తన పుస్తకాల్లో అనేక స్వీకృతాలను ఉపయోగించి అనేక సిద్ధాంతాలను వివరించారు. ఈ సిద్ధాంతాలు యూక్లిడియన్ జ్యామితి అధ్యయనంలో ఇప్పటికీ ఉపయోగించబడుతున్నాయి.
→ రెండు కోణాల మొత్తం 90° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి పూరక కోణాలు అంటారు.
→ రెండు కోణాల మొత్తం 180° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంపూరక కోణాలు అంటారు.
→ రెండు కోణాల మొత్తం 360° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంయుగ్మ కోణాలు అంటారు.
→ రెండు కోణాలు ఉమ్మడి శీర్షం, ఉమ్మడి భుజం కలిగి ఆ రెండు కోణాలు ఉమ్మడి భుజానికి చెరోవైపున ఉన్నచో వాటిని ఆసన్న కోణాలు అంటారు.
→ రెండు ఆసన్న కోణాల మొత్తం 180° అయినచో వాటిని రేఖీయ కోణాల జత లేదా రేఖీయ ద్వయం అని అంటారు.
→ రెండు సరళరేఖలు ఒకదానికొకటి ఖండించుకొన్నప్పుడు, ఆ ఖండన బిందువు వద్ద ఏర్పడిన అభిముఖ కోణాల – జతను శీర్షాభిముఖ కోణాలు అని అంటారు.
→ శీర్షాభిముఖ కోణాలు సమానం.
![]()
→ రెండు లేదా అంతకంటే ఎక్కువ సరళరేఖలను విభిన్న బిందువుల వద్ద ఖండించే సరళరేఖను తిర్యక్ రేఖ అంటారు.
→ ఒక జత సమాంతర రేఖలు p, q లను ఒక తిర్యగ్రేఖ r ఖండించినప్పుడు, ఏర్పడిన కోణాలు ∠1, ∠2, ∠3, ∠4, ∠5, ∠6, ∠7 మరియు ∠8 అని అనుకొనుము.
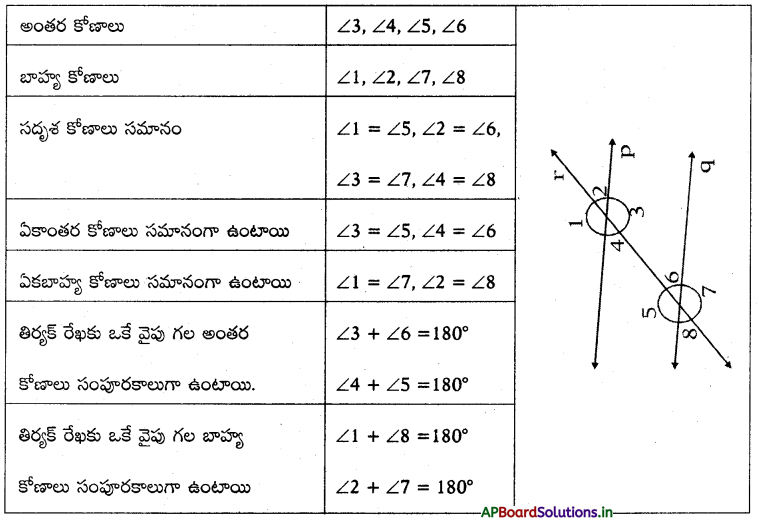
→ ఒక తిర్యక్ రేఖ ఒక జత సరళరేఖలను ఖండించినపుడు,
→ పూరక కోణాలు : రెండు కోణాల మొత్తం 90° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి పూరక కోణాలు అంటారు.
ఉదా : 50° కు పూరకకోణం 40°
అలాగే 40° కు పూరక కోణం 50°
(ఎందుకనగా 50° + 40° = 90°)
x° కు పూరకకోణము 90 – x° అవుతుంది.
→ సంపూరక కోణాలు : రెండు కోణాల మొత్తం 180° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంపూరక కోణాలు అంటారు.
ఉదా : 50° కు సంపూరకకోణం 130°
అలాగే 130° కు సంపూరకకోణం 50°
(ఎందుకనగా 50° + 130° = 180°)
x°కు సంపూరక కోణము 180 – x అవుతుంది.
→ సంయుగ్మ కోణాలు : రెండు కోణాల మొత్తం 360° అయితే, ఆ రెండు కోణాలను ఒకదానికొకటి సంయుగ్మ కోణాలు అంటారు.
ఉదా : 50° కు సంయుగ్మకోణము 310°
అలాగే 310° కు సంయుగ్మకోణము 50°
x° కు సంయుగ్మకోణము 360 – x° అవుతుంది.
→ ఆసన్న కోణాలు : రెండు కోణాలకు ఉమ్మడి శీర్షం, ఉమ్మడి భుజం కలిగి ఆ రెండు కోణాలు ఉమ్మడి భుజానికి చెరోవైపున ఉన్నచో వాటిని ఆసన్న కోణాలు అంటారు.
ఉదా 1:
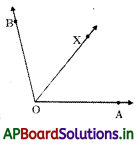
∠AOX మరియు ∠BOXలకు ఉమ్మడి శీర్షము – ‘O’
ఉమ్మడి భుజం – OX
ఉమ్మడి భుజం OXకు ∠AOX మరియు ∠BOX లు చెరొకవైపు కలవు.
కావున ∠AOX మరియు ∠BOX లు ఆసన్న కోణాలు.
ఉదా 2:
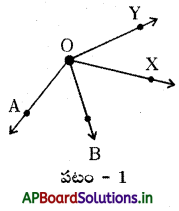
పటం – 1 లో ‘O’ ఉమ్మడి శీర్షం అయితే ∠AOB మరియు ∠XOY లకు ఉమ్మడి భుజం లేదు. కావున ఈ రెండు కోణాలు ఆసన్న కోణాలు కావు.
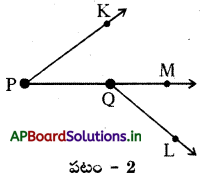
పటం – 2 లో ఉమ్మడి భుజం PM మరియు ∠KPM, ∠MQL లు భుజం PM కు చెరొకవైపు కలవు. కాని రెండు కోణాలకు ఉమ్మడి శీర్చం లేదు.
కావున ∠KPM మరియు ∠MQL లు ఆసన్న కోణాలు కావు.
![]()
→ రేఖీయ కోణాల జత (లేదా) రేఖీయ ద్వయం : రెండు ఆసన్న కోణాల మొత్తం 180° అయినచో వాటిని రేఖీయ కోణాల జత లేదా రేఖీయ ద్వయం అని అంటారు.
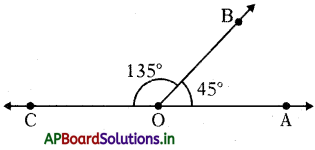
∠AOB మరియు ∠BOC లు ఆసన్న కోణాలు BO మరియు వాని మొత్తం 45° + 135° = 180°.
కావున, ∠AOB మరియు ∠BOC లు రేఖీయ కోణాల జత లేదా రేఖీయ ద్వయం.
ఉదా :
→ శీర్షాభిముఖ కోణాలు : రెండు సరళరేఖలు ఒకదానికొకటి ఖండించుకొన్నప్పుడు, ఆ ఖండన బిందువు వద్ద ఏర్పడిన అభిముఖ (ఆసన్నం కానటువంటి) కోణాలను శీర్షాభిముఖ కోణాలు అని అంటారు.
ఉదా :
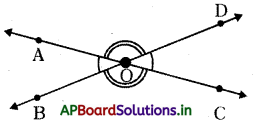
∠AOB, ∠COD లు ఒక జత ∠BOC, ∠AOD లు మరొక జత శీర్షాభిముఖ కోణాలు. శీర్షాభిముఖ కోణాలు ఎప్పటికీ ఆసన్నకోణాల జత కావు. c శీర్షాభిముఖ కోణాలు ఎల్లప్పుడూ సమానము.
→ తిర్యక్ రేఖ : రెండు లేదా అంతకంటే ఎక్కువ సరళరేఖలను విభిన్న బిందువుల వద్ద ఖండించే సరళరేఖను తిర్యక్ రేఖ అంటారు.
ఉదా :
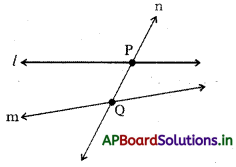
l, m సరళరేఖలను n సరళరేఖ, P మరియు Q అనే వేర్వేరు బిందువుల వద్ద ఖండిస్తున్నది. కావున n తిర్యక్ రేఖ.
→ తిర్యక్ రేఖతో ఏర్పడే కోణాలు, కోణాల జతలు :
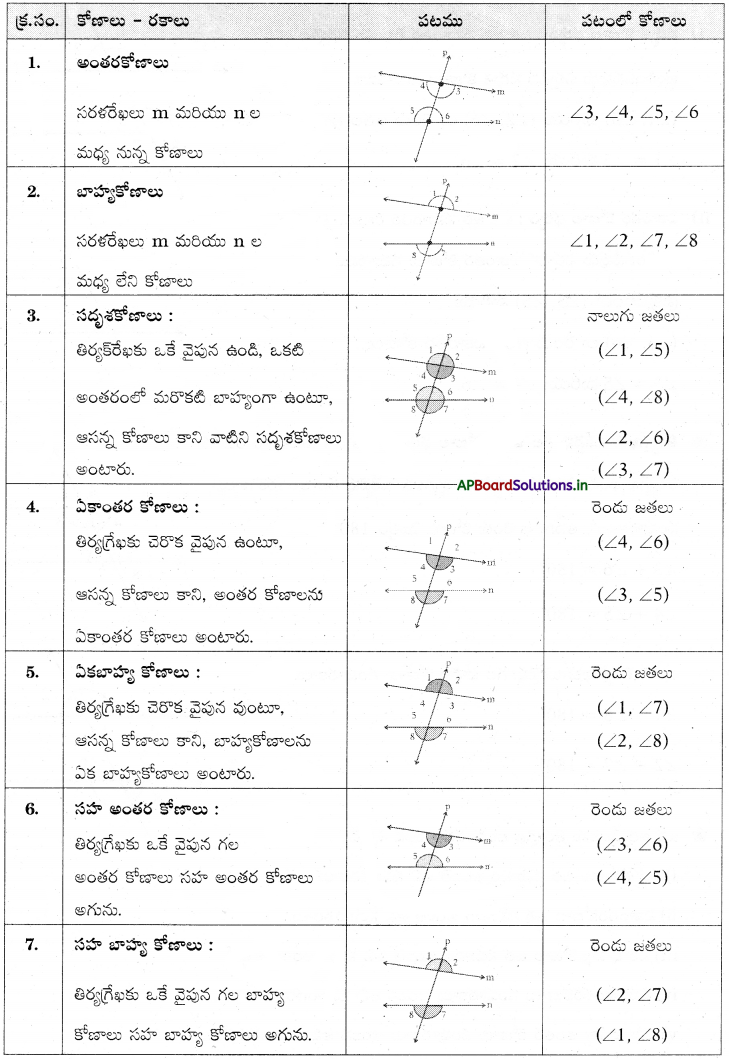
→ సమాంతర రేఖలపై తిర్యగ్రేఖలో ఏర్పడే కోణాల ధర్మాలు :
(i) సదృశ కోణాల ధర్మం : ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన సదృశ కోణాలు సమానము.
(∠1, ∠5) మరియు (∠2, ∠6) లు రెండు జతల సదృశ కోణాలు.
∠1 = ∠5 మరియు 22 = 26.
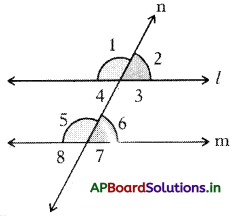
(ii) ఏకాంతర కోణాల ధర్మం : ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన ఏకాంతర కోణాలు సమానము. ప్రక్కపటంలో (∠3, ∠5) మరియు (∠4, ∠6) లు రెండు జతల ఏకాంతర కోణాలు.
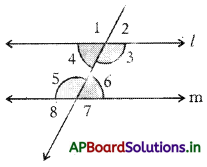
∠3 = ∠5 మరియు ∠4 = ∠6.
→ తిర్యగ్రేఖకు ఒకేవైపు గల అంతరకోణాల ధర్మం : “ఒక జత సమాంతర రేఖలను తిర్యగ్రేఖ ఖండించినపుడు ఏర్పడిన తిర్యగ్రేఖకు, ఒకేవైపు గల అంతరకోణాలు సంపూరకాలు”. అనగా ఆ రెండు కోణాల మొత్తం 180°.
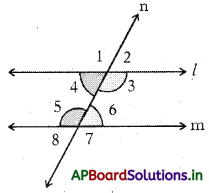
∠3 + ∠6 = 180°
∠4 + ∠5 = 180°
అలాగే తిర్యగ్రేఖకు ఒకేవైపు గల బాహ్య కోణాలు సంపూరకాలు.
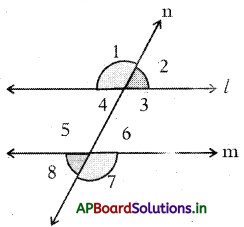
∠1 + ∠8 = 180°
∠2 + ∠7 = 180°
![]()
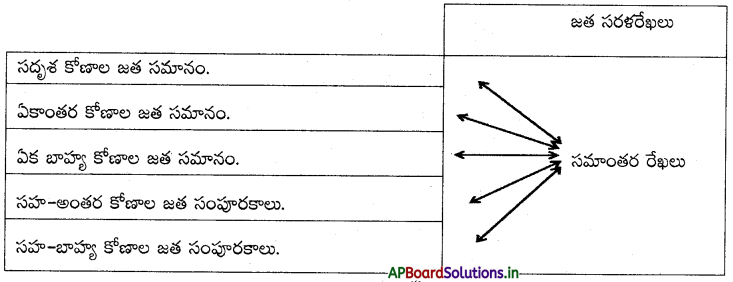
→ ఒక జత రేఖలను తిర్యగ్రేఖ ఖండించడం వలన ఏర్పడే
- సదృశకోణాల జత సమానం అయితే అవి సమాంతరాలు.
- ఏకాంతర కోణాల జత సమానం అయితే అవి సమాంతరాలు.
- ఏక బాహ్య కోణాల జత సమానం అయితే అవి సమాంతరాలు అలాగే
- సహ అంతర కోణాలు సంపూరకాలు అయిన అవి సమాంతరాలు.
- సహ బాహ్య అంతర కోణాలు సంపూరకాలు అయిన అవి సమాంతర రేఖలు.