Students can go through AP Board 7th Class Maths Notes 9th Lesson Algebraic Expressions to understand and remember the concept easily.
AP Board 7th Class Maths Notes 9th Lesson Algebraic Expressions
→ A variable can take various values and its value cannot be fixed. Example : a, b, x, y, z etc., on the other hand a constant has a fixed value. For example 6, 8, -10. etc., are some constants.
→ If every term of an expression is a constant term, then the expression is called a numerical expression.
→ If an expression has at least one algebraic term, then the expression is called an algebraic expression.
→ The terms having the same algebraic factors are like terms and the terms having different algebraic factors are unlike terms.
→ An algebraic expression containing one term is called a monomial. An algebraic expression containing two unlike terms is called a binomial. An algebraic expression containing three unlike terms is called a trinomial.
→ An algebraic expression in which the exponent of the variable is a non-negative integer is called polynomial.
→ In an expression, if the terms are arranged in a manner such that the exponents of the variables are in descending order, then the expression is said to be in standard form.
→ If no two terms of an algebraic expression are alike then, it is said to be in simplified form.
→ The sum of two or more like terms is the sum of the numerical coefficients of all the like terms.
→ The difference between two or more like terms is the difference between the numerical coefficients of the like terms.
→ The value of an expression depends on the different values taken by the variable from which the expression is formed.
![]()
→ Term : Numbers (constants) or variables or combination of both with multiplication or division is a term.
Example : 14, -7, \(\frac{8}{11}\) etc., are numerical terms.
2a, – 5b, 3x2y, \(\frac{3b}{7}\) etc., are variable terms.
→ Expression: An expression is a constant or a. variable or a combination of both using any fundamental operation(s).
Example : 5 + a, 3a -,b, 6, 5x2, 3a + 5b – 6, etc.
→ Numerical expression : If every term of an expression is a constant term, then the expression is a numerical expression.
Example : 14 – 7 + \(\frac{8}{11}\), 5 – 9 + 3 etc.
→ Algebraic expression : If an expression has at least one algebraic term, then the expression is called an algebraic expression.
Example.: 5 + a, 3a – b, 6, 5x2, 3a + 5b – 6, etc.
→ Coefficient : In a term 3xy2,
- 3 is coefficient of xy2
- x is the coefficient of 3y2
- y2 is coefficient of 3x
- 3x is coefficient of y2
- 3y2 is the coefficient of x
- xy2 is the coefficient of 3
Generally in the term 3xy2, 3 is called the numerical coefficient of xy2 and xy2 is the algebraic coefficient of 3.
→ Like terms : Terms having same algebraic factors are called like terms i.e., they differ in numerical coefficients only.
Example : 5x, – 6x, 63x are like terms.
→ Un-like terms : Terms having different algebraic factors are called un-like terms. Example : 5x, – 6x2, -63xy are un-like terms.
→ Types of algebraic expressions: Algebraic expressions are named according to the number of terms in it.
- Monomial : An algebraic expression having only one term is called a Monomial. Example: 3a
- Binomial: An algebraic expression having only two unlike terms is called a Binomial. Example : 3a + 2b
- Trinomial: An algebraic expression having only three unlike terms is called a Trinomial. Example : 3a + 2b – 5c
→ Polynomial: An algebraic expression in which the exponent of each variable is a non¬negative integer is called a polynomial.
Example : 3x2 + 2x – 9, 3x2y – 7y + 2x
5x – 7xy3 + 7, \(\frac{5}{x^{2}}\) + 4xy – 8 are not polynomials, but only algebraic expressions.
Note: All polynomials are algebraic expressions but all algebraic expressions need not necessarily be polynomials.
![]()
→ Addition and subtraction of like terms: To add or subtract like terms we add or subtract their numerical coefficients.
Example : – 3x + 7x = (- 3 + 7)x = 4x also 3x – 8x = (3 – 8)x = – 5x
The sum of two or more like terms is the sum of their numerical coefficients retaining the algebraic factor as it is.
The difference between two or more like terms is the difference between their numerical coefficients retaining the algebraic factor as it is.
→ Simplification of algebraic expressions: If no two terms of an algebraic expression are alike, then it is said to be in its simplified form.
Example: The simplified form of
3x2y – 5xy + 2x2 +5y2 + 8xy – 5x2y is 2x2 – 2x2y + 3xy + 5y2
→ Standard form of an algebraic expression: If in an algebraic expression all the terms are arranged in such a way that the exponents of the terms are in descending order then the expression is said to be in standard form.
Example : Standard form of 3m – 5m2 + 8 is – 5m2 + 3m + 8.
→ Addition and subtraction of algebraic expressions : To add or subtract algebraic expressions we add or subtract their like terms.
It can be done in two ways.
(a) Row method
(b) Column method
Example : To add two or more algebraic expression the like terms of both the expres¬sions are grouped together. The coefficients of like terms are added together and the variable which is common is retained as it is. The unlike terms, are retained as it is and the result obtained is the addition of two or more algebraic expressions.
Example :
Add : 5xy – 3x2 – 12y + 5x, xy – 3x – 12yz + 5x3 and y – 6x2 – zy + 5x3
Answer:
For adding these three algebraic expressions the like terms are grouped together and added as shown below.

→ Subtraction of Algebraic Expressions: To subtract two or more algebraic expressions, it’s a better practice to write the expressions to be subtracted below the expression from which it is to be subtracted from. Like terms are placed below each other. The’ sign of each term which is to be subtracted is reversed and then the resulting expression is added normally.
Example : Subtract x2y – 2x2 – zy + 5 and – 3x2 + 3x3 from y3 + 3x2y – 6x2 – 6zy + 7x3
Answer:
The like terms of the expressions x2y – 2x2 – zy + 5 and – 3x2 + 3x3 are written below the like terms of the expression y3 + 3x2y – 6x2 – 6zy + 7x3.

→ Value of an algebraic expression: To evaluate an algebraic expression means to find the value of the expression when the variable is replaced by a given number. To evaluate an expression, we substitute the given number for the variable in the expression and then simplify the expression using the order of operations.
Example 1 :
Find the value of algebraic expression (p + q + r), if (p = 1), (q = 2) and (r = 3).
Answer:
The given algebraic expression is (p + q + r).
Put the respective values of (p = 1), (q = 2) and (r = 3) in the algebraic expression, and we get:
= 1 + 2 + 3 = 6
![]()
→ Coding and Decoding :
Conversion of information into some symbols and signs is called coding. We can get that information by decoding of those symbols and signs. There are infinite methods of coding and, decoding.*We can check it in different ways.
Let us discuss some methods like symbolic logic, shifting of letters in different patterns, position of letters in alphabetical order.
First we have to prepare one table by assigning numbers to letters in Alphabetical order in both forward and reverse direction. This will help us in decoding of some problems.
Alphabetical number table :
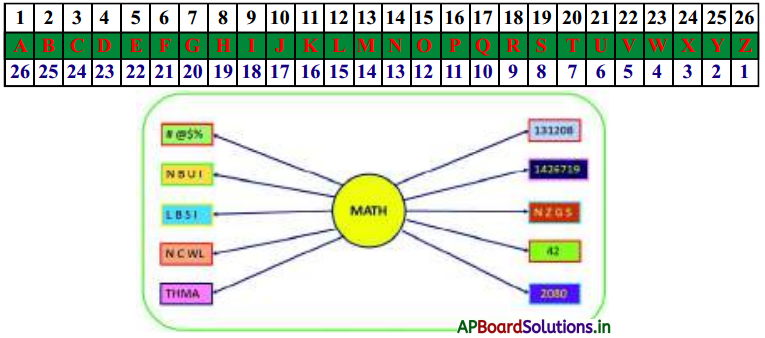
| Method | Example | Explanation |
| 1. Symbolic Logic | In a certain code MATH is written as #@$%, and PAT is written as &@$, then how will be PATH is written in that code? | By comparing each letter with symbol, by writing one below the other,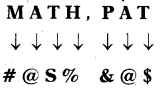 from this, PATH = & @ $% |
| 2. Shifting of letters Forward direction ( + 1 ) | MATH : NBUI, then ROCK:? | In this method, each letter in a word is shifted to 1 position forward in alphabetical order. then, ROCK = SPDL |
| 3. Shifting of letters Forward and Backward direction (-1,+ 1, – 1/ +1 ) | MATH: LBSI,then W I N D : ? | In this method, each letter in a word is shifted to 1 position backward in alphabetical order.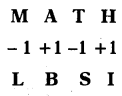 then, W I N D = V J M E |
| 4. Shifting of letters Increasing pattern (+1,+2, + 3,+4) | MATH : NCWL, then FAIR: ? | In this method, each letter in a word is shifted to 1,2,3,4 places in alphabetical order. The logic behind this is ‘ +1’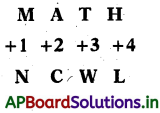 then, FAIR = GCLV |
| 5. Shifting of letters (in different places) | MATH: THMA, then BOOK:? | First write numbers below the given word, then observe the pattern. Follow the same to decode the given word.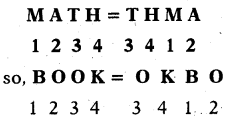 |
| 6. Position of letters: (as per alphabetical order) | MATH: 131208, then NOTE:? | In the above alphabetic number table, the numbers of corresponding letters are taken in forward,
(M =13, A = 1, T = 20, H = 8) so, NOTE = 1415205 |
| 7. Position of letters: (in reverse) | MATH : 1426719, then LIFE:? | The numbers corresponding letters taken in reverse position (M = 14, A= 26, T = 7, H = 19) So, LIFE = 15182122 |
| 8. Position of letters: (same position but in reverse direction) | M A T H : N Z G S, then SONG : ? | Taking the letters from same positions,but in reverse direction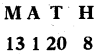 the letters in 13, 1, 20, 8 positions are N Z G S. so, SONG = HLMT |
| 9. Sum of positions (in forward direction) | M A T H: 42, then BEAT:? | Taking sum of positions of letters in forward direction, 13 + 1+20 + 8 = 42 So, BEAT = 2 + 5 + 1+20 = 28 |
| 10. Product of positions | MATH: 2080, then LINE:? | Taking product of positions of letters in forward direction MATH = (13)( 1 )(20)(8) = 2080, So, LINE= (12)(9)(14)(5) = 7560 |