SCERT AP 7th Class Maths Solutions Pdf Chapter 2 Fractions, Decimals and Rational Numbers Review Exercise Questions and Answers.
AP State Syllabus 7th Class Maths Solutions 2nd Lesson Fractions, Decimals and Rational Numbers Review Exercise
Question 1.
Write the following fractions in ascending order.
(i) \(\frac{3}{2}, \frac{5}{2}, \frac{1}{2}, \frac{17}{2}, \frac{9}{2}\)
Answer:
Given \(\frac{3}{2}, \frac{5}{2}, \frac{1}{2}, \frac{17}{2}, \frac{9}{2}\)
Given fractions are like fractions.
So, we should arrange the numerators in ascending order.
\(\frac{1}{2}<\frac{3}{2}<\frac{5}{2}<\frac{9}{2}<\frac{17}{2}\)
Ascending order: \(\frac{1}{2}<\frac{3}{2}<\frac{5}{2}<\frac{9}{2}<\frac{17}{2}\)
(ii) \(\frac{6}{5}, \frac{11}{10}, \frac{19}{5}, \frac{7}{10}, \frac{5}{10}\)
Answer:
Given \(\frac{6}{5}, \frac{11}{10}, \frac{19}{5}, \frac{7}{10}, \frac{5}{10}\)
Given fractions are not like fractions. So, first we have to convert them into like fractions.
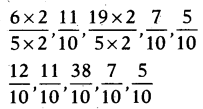
Now arrange them in ascending order according to their numerators.
\(\frac{5}{10}<\frac{7}{10}<\frac{11}{10}<\frac{12}{10}<\frac{38}{10}\)
Ascending order: \(\frac{5}{10}<\frac{7}{10}<\frac{11}{10}<\frac{12}{10}<\frac{38}{10}\)
(iii) \(\frac{8}{3}, \frac{7}{6}, 3 \frac{1}{4}, \frac{5}{3}, \frac{11}{4}\)
Answer:
Given \(\frac{8}{3}, \frac{7}{6}, 3 \frac{1}{4}, \frac{5}{3}, \frac{11}{4}\)
\(\frac{8}{3}, \frac{7}{6}, \frac{13}{4}, \frac{5}{3}, \frac{11}{4}\)
We have to find the LCM of denominators to convert them into equal fraction.
LCM of numerators is 12

Now arrange the like fractions in ascending order according to their numerators.
\(\frac{14}{12}<\frac{20}{12}<\frac{32}{12}<\frac{33}{12}<\frac{39}{12}\)
Ascending order :
\(\frac{14}{12}<\frac{20}{12}<\frac{32}{12}<\frac{33}{12}<\frac{39}{12}\)
![]()
Question 2.
Calculate the following.
(i) \(\frac{3}{5}+\frac{7}{4}\)
Answer:
Given \(\frac{3}{5}+\frac{7}{4}=\frac{12+35}{20}=\frac{47}{20}\)
(ii) \(\frac{5}{6}+\frac{7}{12}\)
Answer:
Given \(\frac{5}{6}+\frac{7}{12}\)
= \(\frac{5 \times 2}{6 \times 2}+\frac{7}{12}\)
= \(\frac{10}{12}+\frac{7}{12}\)
= \(\frac{10+7}{12}=\frac{17}{12}=1 \frac{5}{12}\)
(iii) 1\(\frac{7}{8}-\frac{1}{5}\)
Answer:
Given 1\(\frac{7}{8}-\frac{1}{5}\)

(iv) 4\(\frac{1}{2}\) + 3\(\frac{1}{3}\)
Answer:
Given 4\(\frac{1}{2}\) + 3\(\frac{1}{3}\)

Question 3.
Simplify the following.
(i) \(\frac{1}{4}\) of 3
Answer:
Given \(\frac{1}{4}\) of 3
= \(\frac{1}{4} \times \frac{3}{1}=\frac{3}{4}\)
(ii) \(\frac{5}{8}\) of \(\frac{2}{3}\)
Answer:
Given \(\frac{5}{8}\) of \(\frac{2}{3}\)

(iii) \(\frac{15}{4} \times 2 \frac{1}{7}\)
Answer:
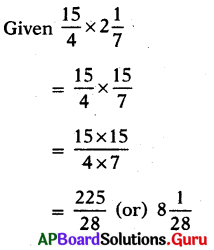
(iv) 3\(\frac{1}{3}\) × 2\(\frac{2}{5}\)
Answer:
Given 3\(\frac{1}{3}\) × 2\(\frac{2}{5}\)
= \(\frac{10}{3} \times \frac{12}{5}\)
= \(\frac{120}{15}=\frac{8}{1}\) = 8
![]()
Question 4.
Calculate the following.
(i) \(\frac{3}{4}\) ÷ 3
Answer:
Given \(\frac{3}{4}\) ÷ 3
= \(\frac{3}{4}\) ÷ \(\frac{3}{1}\)
We know reciprocial of \(\frac{3}{1}\) is \(\frac{1}{3}\)
= \(\frac{3}{4} \times \frac{1}{3}\)
= \(\frac{3}{12}\) (or) \(\frac{1}{4}\)
(ii) 8 ÷ 2\(\frac{1}{7}\)
Answer:
Given 8 ÷ 2\(\frac{1}{7}\)
= 8 ÷ 2\(\frac{15}{7}\)
We know reciprocial of \(\frac{15}{7}\) is \(\frac{7}{15}\)
= 8 × \(\frac{7}{15}\)
= \(\frac{8 \times 7}{15}\)
= \(\frac{56}{15}\) (OR) 3\(\frac{11}{15}\)
(iii) \(\frac{12}{7} \div \frac{2}{7}\)
Answer:
Given \(\frac{12}{7} \div \frac{2}{7}\)
We know reciprocial of \(\frac{12}{7} \div \frac{2}{7}\)
= \(\frac{12}{7} \times \frac{7}{2}\)
= \(\frac{12 \times 7}{7 \times 2}=\frac{84}{14}=\frac{6}{1}\) = 6
(iv) 5\(\frac{1}{2}\) ÷ 2\(\frac{9}{11}\)
Answer:
Given 5\(\frac{1}{2}\) ÷ 2\(\frac{9}{11}\)
= \(\frac{11}{2} \div \frac{31}{11}\)
We know reciprocial of \(\frac{31}{11}\) is \(\frac{11}{31}\)
= \(\frac{11}{2} \times \frac{11}{31}\)
= \(\frac{121}{62}\) (OR) 1\(\frac{59}{62}\)