AP 9th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు

Students can go through AP Board 9th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు to understand and remember the concept easily.

AP Board 9th Class Maths Notes 1st Lesson వాస్తవ సంఖ్యలు

→ వివిధ రకాల సంఖ్యల యొక్క వరుస క్రమము :

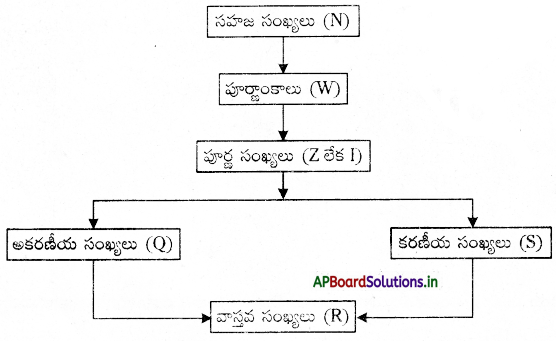
→ సహజ సంఖ్యలు : లెక్కించు సంఖ్యలను సహజ సంఖ్యలు అంటారు. వీటిని N తో సూచిస్తారు.
N = {1, 2, 3, 4, ………..}

→ పూర్ణాంకాలు : అన్ని సహజ సంఖ్యలు మరియు ‘0’ కూడా ఉంటే ఆ సంఖ్యలను పూర్ణాంకాలు అంటారు.
W = {0, 1, 2, 3, ……….}

→ పూర్ణ సంఖ్యలు : పూర్ణాంకాలు మరియు ఋణ సహజ సంఖ్యలను కలిపి పూర్ణ సంఖ్యలంటారు.

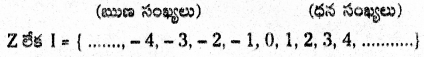
అకరణీయ సంఖ్యలు:
→ p/q రూపంలో రాయగల సంఖ్యలను అకరణీయ సంఖ్యలు అంటారు. ఇక్కడ p, q లు పూర్ణ సంఖ్యలు మరియు q ≠ 0.

→ అకరణీయ సంఖ్యలను ‘Q’ అనే అక్షరంచే సూచిస్తారు.

→ ప్రతీ సహజ సంఖ్య, పూర్ణాంకం మరియు పూర్ణ సంఖ్య ఒక అకరణీయ సంఖ్య అవుతుంది.

→ ఏవైనా రెండు పూర్ణ సంఖ్యల మధ్యన అనంతమైన అకరణీయ సంఖ్యలను ఉంచవచ్చును.
ఉదా:
: 3 < \(\frac{19}{6}, \frac{20}{6}, \frac{21}{6}, \frac{22}{6}, \frac{23}{6}\), ………………< 4

→ ప్రతి పూర్ణసంఖ్య ఒక అకరణీయ సంఖ్య అగును. కానీ ప్రతి అకరణీయ సంఖ్య ఒక పూర్ణసంఖ్య కాదు.

→ సున్నా ఒక అకరణీయ సంఖ్యయే.
ఉదా : \(\frac{0}{2}, \frac{0}{3}, \frac{0}{7}, \frac{0}{13}\), ………………….

→ ఏ రెండు అకరణీయ సంఖ్యల మధ్యనైనా అనంతమైన అకరణీయ సంఖ్యలను ఉంచవచ్చును.
ఉదా – \(\frac{3}{4}<\frac{29}{8}<\frac{71}{16}<\frac{81}{14} \ldots \ldots \ldots<\frac{13}{2}\)

→ ఒక అకరణీయ సంఖ్య యొక్క దశాంశ రూపము అనునది ఆ సంఖ్యలోని లవమును హారముచే భాగించగా ఏర్పడును.
ఉదా : \(\frac{5}{6}\) యొక్క దశాంశ రూపము

∴ \(\frac{5}{6}\) = 0.83 ….. = \(0.8 \overline{3}\)

→ ప్రతి అకరణీయ సంఖ్యను అంతమయ్యే దశాంశంగాను లేదా అంతంకాని దశాంశంగానూ వ్రాయవచ్చును.
ఉదా : \(1 . \overline{62}=\frac{161}{99}\)

→ ఒక కనిష్ఠ రూపంలోని భిన్నం అంతమయ్యే దశాంశ భిన్నం లేదా అంతంలేని ఆవర్తిత దశాంశ భిన్నం కావాలంటే ఆ భిన్నం యొక్క హారాన్ని ప్రధాన కారణాంకాల లబ్దంగా వ్రాసి నియమాన్ని రాబట్టవచ్చును.
ఉదా : \(\frac{13}{32}\) ను అంతమగు దశాంశ భిన్నంగా వ్రాయవచ్చును.

కరణీయ సంఖ్యలు:
→ రూపంలో రాయలేని సంఖ్యలను కరణీయ సంఖ్యలంటారు. ఇక్కడ p, q లు పూర్ణ సంఖ్యలు మరియు q ≠ 0.
ఉదా : √2, √3, √5, ….. మొ||నవి.

→ కరణీయ సంఖ్యలను ‘S’ లేదా Q’ తో సూచిస్తారు.

→ కరణీయ సంఖ్యలు అంతము మరియు ఆవర్తితం కాని దశాంశాలు.

→ క్రీ.పూ. 5వ శతాబ్దంలో పైథాగోరియన్ అను పైథాగరస్ అనుయాయులు మొదటగా కరణీయ సంఖ్యలను కనుగొని వాటికి పేరు పెట్టారు.

→ కరణీయ సంఖ్యలను పైథాగరస్ సిద్ధాంతముననుసరించి సంఖ్యారేఖపై సూచిస్తారు.
ఉదా : √2 ను సంఖ్యారేఖపై సూచించుట.

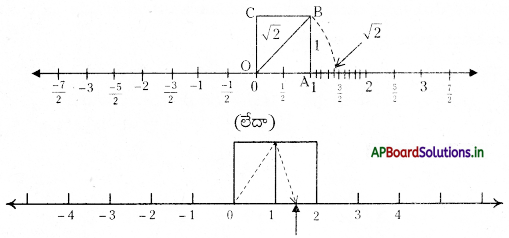
√2 ≅ 1.4142135

→ ‘n’ ఒక సంపూర్ణవర్గం కాని సహజ సంఖ్య అయితే √n ఒక కరణీయ సంఖ్య అవుతుంది.
ఉదా : 2, 3, 5, 7, 8, ……… మొ||నవి సంపూర్ణ వర్గాలు కావు.
∴ √2, √3, √5, √7 మరియు √8 లు కరణీయ సంఖ్యలు.

→ మనం తరచుగా \(\frac{22}{7}\) ను π. విలువకు ఉజ్జాయింపుగా తీసుకుంటాము కాని π ≠ \(\frac{22}{7}\)

→ ఏదైనా ధన పూర్ణసంఖ్య nకు \(\sqrt{n-1}\) ను సంఖ్యారేఖపై సూచించిన తరువాత √n ను సూచించవచ్చును.

→ కరణీయ సంఖ్యలు మరియు అకరణీయ సంఖ్యల సముదాయాన్ని వాస్తవ సంఖ్యలు అని అంటాము.

→ సంఖ్యారేఖపై ప్రతి బిందువుకు సదృశ్యంగా ఏకైక వాస్తవ సంఖ్య ఉంటుంది. అదే విధముగా ప్రతి వాస్తవ సంఖ్యకు సదృశ్యంగా సంఖ్యారేఖపై ఏకైక బిందువు ఉంటుంది.

→ ‘l’ ఒక అకరణీయ సంఖ్య మరియు ‘m’ ఒక కరణీయ సంఖ్య అయితే 1 + m, l-m, lm మరియు \(\frac{l}{m}\) లన్నీ కరణీయ సంఖ్యలే.
ఉదా : 7 మరియు √5 ⇒ 7+ √5, 7 – √5, 7√5 మరియు \(\frac{7}{\sqrt{5}}\) లన్నీ కరణీయ సంఖ్యలే.

→ ab ఒక సంపూర్ణ వర్గం కాకుండునట్లు a, b లు ఏవైనా రెండు ధన అకరణీయ సంఖ్యలయితే \(\sqrt{ab}\) అనునది a, bల మధ్య ఉండే కరణీయ సంఖ్య అవుతుంది.

ఉదా : 7 మరియు 4 లు ఏవైనా రెండు అకరణీయ సంఖ్యలు అనుకొనుము.
7 × 4 = 28 కచ్చిత వర్గము కాదు, కాబట్టి \(\sqrt{28}\) విలువ 7 మరియు 4 ల మధ్యనుండును.
అదే విధంగా 4 < \(\sqrt{28}\) < 7.

→ రెండు కరణీయ సంఖ్యల లబ్దము అకరణీయ సంఖ్య అయిన ఆ రెండు సంఖ్యలు ఒకదానికొకటి అకరణీయ కారణాంకాలు అవుతాయి.
ఉదా : 7√3 మరియు 5√3 లు ఏవైనా రెండు కరణీయ సంఖ్యలైన 7√3 × 5√3 = 7 × 5 × 3 = 105 ఒక అకరణీయ సంఖ్య.

→ కరణీయ సంఖ్యలు సంకలనము, వ్యవకలనము, గుణకారము మరియు భాగహారాల దృష్ట్యా సంవృత ధర్మాన్ని పాటించను.

→ (a ± √b) అను అకరణీయ సంఖ్య యొక్క సాధారణ అకరణీయ కారణాంక రూపము (a ∓ √b) అగును. వీటిని ఒకదానికొకటి అకరణీయ కారణాంకాలు అంటారు.

→ ఘాతాంక న్యాయాలు : a > 0 ఒక ధన వాస్తవ సంఖ్య మరియు m, n లు రెండు అకరణీయ సంఖ్యలు అయితే
(i) a^m. aⁿ = a^m+n
ఉదా : 5⁴ . 5^-3 = 5^{4 + (-3)} = 5¹ = 5

(ii) (a^m)ⁿ = a^mn
ఉదా : (4³)² = 4^3×2 = 4⁶

(iii) \(\frac{a^{m}}{a^{n}}\) = a^m-n అయితే
= 1 ; m = n అయితే
= \(\frac{1}{a^{n-m}}\); m < n అయితే

(iv) a^m. bⁿ = (ab)^m
ఉదా : (-5)³ (2)³ = (-5 × 2)³ = (- 10)³

(v) \(\frac{1}{a^{n}}\) = a^-n
ఉదా : \(\frac{1}{216}=\frac{1}{6^{3}}\) = 6^-3

(vi) a° = 1
\(\left(\frac{-3}{4}\right)^{0}\) = 1

→ a, b లు ఏవైనా రెండు వాస్తవ సంఖ్యలు అయితే

• \(\sqrt{ab}\) = √a . √b
• \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\), b ≠ 0
• (√ a + √b)(√a – √b) = a – b
• (a + √b) (a – √b) = aి – b
• (√a + √b)(√c + √d) = \(\sqrt{\mathrm{ac}}+\sqrt{\mathrm{ad}}+\sqrt{\mathrm{bc}}+\sqrt{\mathrm{bd}}\)
• (√a + √b) = a + 2\(\sqrt{ab}\) + b

→ a, b లు పూర్ణ సంఖ్యలైన \(\frac{1}{\sqrt{a}+b}\) యొక్క హారాన్ని అకరణీయం చేయడానికి లవ, హారాలను √a – b చే గుణించాలి.

→ a > 0 మరియు n > 1 అయితే \(\sqrt[n]{a}\) లేదా a^1/n ను nవ పరిమాణ కరణి అని అంటారు.

→ \(\sqrt[n]{a}\) లో ‘a’ ను రాడికెండ్ అని, \(\sqrt[n]{ }\) ను రాడికల్ అని మరియు ‘n’ ను రాడికల్ పరిమాణం అని అంటాము.

→ కరణి యొక్క ఘాత రూపము a^1/n, రాడికల్ రూపము \(\sqrt[n]{a}\).

ఉదాహరణ – 1:
\(\frac{5}{3}\) మరియు – \(\frac{5}{3}\) లను సంఖ్యారేఖ పై సూచించండి.
జవాబు :
– 2, -1, 0, 1, 2 లను సూచిస్తూ ఒక పూర్ణ సంఖ్యారేఖ గీయండి.

సున్నాకు కుడి మరియు ఎడమల వైపు ప్రతి యూనిట్ ను మూడు సమాన భాగాలుగా చేయండి. ఇందు నుంచి 5 భాగాలను తీసుకోండి. సున్నా నుంచి కుడివైపుగల ఐదవ బిందువు \(\frac{5}{3}\)ను మరియు ఎడమవైపుగల ఐదవ బిందువు –\(\frac{5}{3}\) ను సూచిస్తుంది.

ఉదాహరణ – 2:
కింది వాక్యాలలో సరియైనవి ఏవి ? మీ జవాబును ఒక ఉదాహరణతో సమర్థించండి.
(i) ప్రతి అకరణీయ సంఖ్య ఒక పూర్ణ సంఖ్య అవుతుంది.
జవాబు :
సరికాదు. ఉదాహరణకు \(\frac{7}{8}\) ఒక అకరణీయ సంఖ్య కాని పూర్ణ సంఖ్య కాదు.

(ii) ప్రతి పూర్ణ సంఖ్య ఒక అకరణీయ సంఖ్య అవుతుంది.
జవాబు :
సరియైనది. ఎందుకంటే ఏ పూర్ణ సంఖ్యనయినా \(\frac{p}{q}\) (q ≠ 0) రూపంలో రాయవచ్చు. ఉదాహరణకు – 2 ఒక పూర్ణ సంఖ్య – 2 = \(\frac{-2}{1}=\frac{-4}{2}\) ఒక అకరణీయ సంఖ్య. (ఏదేని పూర్ణసంఖ్య ‘D’ ని \(\frac{b}{1}\) ‘గా రాయవచ్చు.)

(iii) సున్నా ఒక అకరణీయ సంఖ్య.
జవాబు :
సరియైనది. ఎందుకంటే 0 ను \(\frac{0}{2}, \frac{0}{7}, \frac{0}{13}\) గా రాయవచ్చు. (0′ ను \(\frac{0}{x}\) గా రాయవచ్చు. ఇక్కడ ‘x’ పూర్ణసంఖ్య మరియు x ≠ 0)

ఉదాహరణ – 3:
3 మరియు 4 ల మధ్య రెండు అకరణీయ సంఖ్యలను సగటు పద్ధతిలో కనుగొనండి.
జవాబు :
1వ పద్ధతి : a మరియు b ల మధ్య \(\frac{a+b}{2}\) అను అకరణీయ సంఖ్య ఉంటుంది.
ఇక్కడ 2 = 3 మరియు b = 4, (\(\frac{a+b}{2}\) , ‘a’, ‘b’ల సగటు అని, అది ‘a’, ‘b’ల మధ్య ఉండునని మనకు తెలుసు.
కాబట్టి, (\(\frac{3+4}{2}\)) = \(\frac{7}{2}\) అను అకరణీయ సంఖ్య 3 మరియు 4 ల మధ్య ఉంటుంది. 3 < \(\frac{7}{2}\) <4 ఈ పద్ధతిని కొనసాగిస్తే 3 మరియు 4 ల మధ్య మరికొన్ని అకరణీయ సంఖ్యలనుంచవచ్చు.

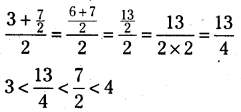
2వ పద్ధతి : మరొక సులభమయిన పద్ధతిని గమనిద్దాం. .. మనం రెండు అకరణీయ సంఖ్యలుంచాలి కాబట్టి 3, 4లను 2 + 1 = 3 హారాలుగా గల అకరణీయ సంఖ్యలుగా రాస్తాము.
అనగా 3 = \(\frac{3}{1}=\frac{6}{2}=\frac{9}{3}\) మరియు
4 = \(\frac{4}{1}=\frac{8}{2}=\frac{12}{3}=\frac{16}{4}\)
కాబట్టి 3 మరియు 4ల మధ్య \(\frac{10}{3}, \frac{11}{3}\) లు రెండు అకరణీయ సంఖ్యలు అవుతాయి.
3 = \(\frac{9}{3}<\left(\frac{10}{3}<\frac{11}{3}\right)<\frac{12}{3}\) = 4
ఇప్పుడు మనం 3, 4 ల మధ్య ఐదు అకరణీయ సంఖ్యలుంచాలి అంటే 3, 4 లను 5 + 1 = 6 హారాలుగా గల అకరణీయ సంఖ్యలుగా రాస్తాము.

అనగా 3 = \(\frac{18}{6}\) మరియు 4 = \(\frac{24}{6}\)
3 = \(\frac{18}{6}<\left(\frac{19}{6}, \frac{20}{6}, \frac{21}{6}, \frac{22}{6}, \frac{23}{6}\right)<\frac{24}{6}\) = 4

ఈ విధంగా 3, 4ల మధ్య అనంతమయిన అకరణీయ సంఖ్యలుంటాయని మనకు తెలుస్తుంది. మరి ఏవైనా రెండు వేరే అకరణీయ సంఖ్యల మధ్య కూడా ఇదే విధంగా లెక్కలేనన్ని అకరణీయ సంఖ్యలుంటాయని చూపవచ్చా ? ప్రయత్నించండి. దీని నుంచి మనం ఏ రెండు అకరణీయ సంఖ్యల మధ్యనైనా అనంతమైన సంఖ్యలో అకరణీయ సంఖ్యలు వ్యవస్థితమవుతాయని చెప్పవచ్చు.

ఉదాహరణ – 4:
\(\frac{7}{16}, \frac{2}{3}\) మరియు \(\frac{10}{7}\) లను దశాంశ భిన్నాలుగా రాయండి
జవాబు :

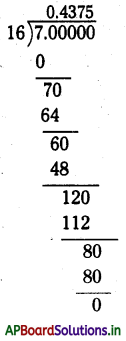
∴ \(\frac{7}{16}\) = 0.4375 అంతమయ్యే దశాంశం

∴\(\frac{10}{7}=1 . \overline{428571}\) అంతంకాని ఆవర్తిత దశాంశం

∴ \(\frac{2}{3}\) = 0.666 = \(0 . \overline{6}\) అంతంకాని ఆవర్తిత దశాంశం

ఉదాహరణ – 5:
3.28 ని \(\frac{p}{q}\) రూపంలో రాయండి. (ఇక్కడ q ≠ 0 మరియు p, q లు పూర్ణ సంఖ్యలు).
జవాబు :

ఉదాహరణ – 6:
\(1 . \overline{62}\)ను \(\frac{p}{q}\) రూపంలో రాయండి. p, q లు పూర్ణసంఖ్యలు మరియు q ≠ 0.
జవాబు :
x = 1.626262 ….. (1) అనుకొనుము.

సమీకరణం (1)ని ఇరువైపులా 100 చే గుణించగా
100x = 162.6262 . . ….. (2)

సమీకరణం (2) నుంచి (1) ని తీసివేయగా

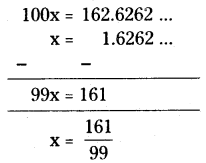
x = \(\frac{161}{99}\)
∴ \(1 . \overline{62}=\frac{161}{99}\)

ఉదాహరణ – 7:
√2 ను సంఖ్యారేఖపై సూచించండి.
జవాబు :
ఒక యూనిట్ భుజముగాగల చతురస్రం OABC ని సంఖ్యారేఖపై 0 వద్ద గీయండి.
పైథాగరస్ సిద్ధాంతం ప్రకారం OB = \(\sqrt{1^{2}+1^{2}}=\sqrt{2}\)

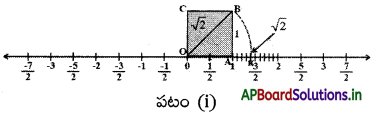
OB = √2 అని మనకు తెలుసు. ఒక వృత్తలేఖినిని ఉపయోగించి 0 కేంద్రంగా OB వ్యాసార్ధంతో సంఖ్యారేఖపై 0 కు కుడివైపున K వద్ద ఖండించునట్లుగా ఒక చాపాన్ని గీయండి.
K అనునది సంఖ్యారేఖపై √2 ను సూచిస్తుంది.

ఉదాహరణ – 8:
√3ను సంఖ్యారేఖపై సూచించండి.
జవాబు :
పటం (i) ను ఒకసారి గుర్తుకు తెచ్చుకోండి.

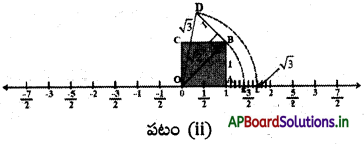
పటం (ii) లో 1 యూనిట్ ప్రమాణంలో BD ని OB కి లంబంగా ఉండే విధంగా గీయండి. 0, D లను కలపండి.

పైథాగరస్ సిద్ధాంతము ప్రకారం
OD = \(\sqrt{(\sqrt{2})^{2}+1^{2}}=\sqrt{2+1}=\sqrt{3}\)

ఒక వృత్తలేఖినిని ఉపయోగించి 0 కేంద్రంగా OD వ్యాసార్ధంతో సంఖ్యారేఖపై 0 కు కుడివైపున ‘L’ వద్ద ఖండించునట్లు ఒక చాపాన్ని గీయండి. ‘L’ అనునది సంఖ్యారేఖపై √3 ను సూచిస్తుంది. ఈ విధంగా ఏదైనా ధనపూర్ణసంఖ్య n కు \(\sqrt{n-1}\) ను సంఖ్యారేఖ పై సూచించిన తరువాత √n ను సూచించవచ్చు.

ఉదాహరణ – 9:
\(\frac{1}{5}\) మరియు \(\frac{2}{7}\)ల మధ్యగల పై రెండు కరణీయ సంఖ్యలు కనుగొనండి
జవాబు :
\(\frac{1}{5}\) = 0.20 అని మనకు తెలుసు.
\(\frac{2}{7}\) = 0.285714
\(\frac{1}{5}\) మరియు \(\frac{2}{7}\)ల దశాంశ రూపాలను పరిశీలించండి.
ఈ రెండింటి మధ్య అనంతమయిన కరణీయ సంఖ్యలు ఉంచవచ్చు.

ఉదాహరణకు …..
0.201201120111 …..
0.24114111411114……
0.25231617181912 ………….
0.267812147512 …..
ఇలాగే \(\frac{1}{5}\) మరియు \(\frac{2}{7}\)ల మధ్య మరో నాలుగు కరణీయ సంఖ్యలు రాయగలవా?

ఉదాహరణ – 10:
3 మరియు 4 ల మధ్యగల ఒక కరణీయ సంఖ్యను రాయండి.
జవాబు :
ab ఒక సంపూర్ణ వర్గం కాకుండునట్లు a, b లు ఏవయినా రెండు ధన అకరణీయ సంఖ్యలయితే \(\sqrt{ab}\) అనునది a, b ల మధ్య ఉండే కరణీయ సంఖ్య అవుతుంది.

∴3 మరియు 4 ల మధ్య కరణీయ సంఖ్య
= \(\sqrt{3 \times 4}\) = √3 × √4
= √3 × 2 = 2√3

ఉదాహరణ – 11:
కింది లబ్దాలు కరణీయ సంఖ్యలు అవుతాయో లేక అకరణీయ సంఖ్యలవుతాయో తెలపండి.
(i) (3 + √3) + (3 – √3)
జవాబు :
(3 + √3) + (3 – √3)
= 3 + √3 + 3 – √3
= 6, ఒక అకరణీయ సంఖ్య.

(ii) (3 + √3) (3 – √3)
జవాబు :
(3 + √3) (3 – √3)
(a + b) (a – b) = a² – b² అని మనకు తెలుసు.
(3+ √3) (3 – √3) = 3² – (√3)²
= 9 – 3 = 6,
ఒక అకరణీయ సంఖ్య.

(iii) \(\frac{10}{2 \sqrt{5}}\)
జవాబు :
\(\frac{10}{2 \sqrt{5}}=\frac{10 \div 2}{2 \sqrt{5} \div 2}=\frac{5}{\sqrt{5}}=\frac{\sqrt{5} \times \sqrt{5}}{\sqrt{5}}\) = √5

(iv) (√2 + 2)²
జవాబు :
(2 + 2)² = (√2)² + 2.√2.2 + 2²
= 2 + 4√2 + 4 = 6 + 4√2, కరణీయ సంఖ్య.

ఉదాహరణ-12:
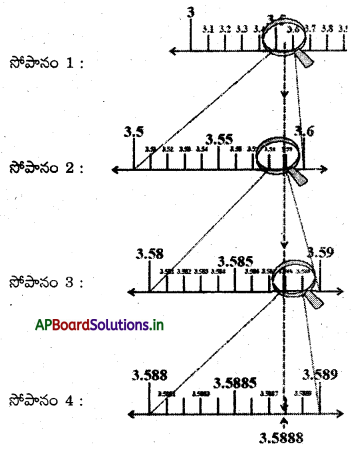
\(3.5 \overline{8}\)ను 4 దశాంశ స్థానాల వరకు క్రమానుగత వర్ధన పద్ధతిలో సంఖ్యారేఖపై చూపించండి.
జవాబు :
క్రమానుగత వర్ధన పద్ధతిని 3.5888 ని గుర్తించండి.

ఉదాహరణ – 13:
(i) 5√2
(ii) \(\frac{5}{\sqrt{2}}\)
(iii) 21 + √3
(iv) π + 3లు
కరణీయ సంఖ్యలవుతాయేమో చూడండి.
జవాబు :
√2 = 1.414 …, √3 = 1.732 …, π, = 3.1415…. అని మనకు తెలుసు.
(i) 5√2 = 5(1.414 …) = 7.070 ….

(ii) \(\frac{5}{\sqrt{2}}=\frac{5}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}=\frac{5 \sqrt{2}}{2}=\frac{7.070}{2}\)
= 3.535 … (i నుంచి)

(iii) 21 + √3 = 21 + 1.732 = 22.732 ….

(iv) π + 3 = 3.1415 …. + 3 = 6.1415

q అకరణీయ సంఖ్య. S కరణీయ సంఖ్యలయితే q + s, q – s, as మరియు \(\frac{q}{s}\) (s ≠ 0) లన్నీ కరణీయ సంఖ్యలే.
ఇవన్నీ అంతము మరియు ఆవర్తితం కాని దశాంశాలు. కాబట్టి ఇవి కరణీయ సంఖ్యలు.

ఉదాహరణ – 14:
5√3 + 7√5. ను 3√5 – 7√3 నుండి తీసివేయండి.
జవాబు :
(3√5 -7√3) – (5√3 + 7√5)
= 3√5 – 7√3 – 5√3 – 7√5
= -4√5 – 12√3
= – (4√5 + 12√3)

ఉదాహరణ – 15:
6√3ను 13√3 తో గుణించండి.
జవాబు :
6√3 x 13√3 = 6 x 13 x √3 x √3
= 78 x 3 = 234
వర్గమూలాలకు సంబంధించిన కొన్ని ధర్మాలు కింద ఇవ్వబడినవి.
a, b లు ఏవైనా రెండు వాస్తవసంఖ్యలు అయితే

• \(\sqrt{ab}\) = √a√b
• \(\sqrt{\frac{a}{b}}=\frac{\sqrt{a}}{\sqrt{b}}\); అయితే b ≠ 0
• (√a + √b) (√a – √b) = a – b
• (a + √b) (a – √b) = a² – b
• (√a + √b) (√c + √d) = \(\sqrt{a c}+\sqrt{a d}+\sqrt{b c}+\sqrt{b d}\)
• (√a + √b)² = a + 2\(\sqrt{ab}\) + b

ఈ ధర్మాలనుపయోగించే వివిధ సందర్భాలను ఇప్పుడు మనం చూద్దాం.

ఉదాహరణ – 16:
కింది సమాసాలను సూక్ష్మీకరించండి.
(i) (3 + √3) (2 + √2)
జవాబు :
(3 + √3) (2 + √2)
= 6+ 3√2 + 2√3 + √6

(ii) (2 + √3) (2 – √3),
జవాబు :
(2 + √3) (2 – √3) = 2² – (√3)²
= 4 – 3 = 1

(iii) (√5 + √2)
జవాబు :
(√5 + √2)²
= (√5)² + 2√5√2 + (√2)²
= 5 + 2√10 + 2 = 7 + 2/10

(iv) (√5 – √2) (√5 + √2)
జవాబు :
(√5 – √2) (√5 + √2)
= (√5)² – (√2)² = 5 – 2 = 3

ఉదాహరణ – 17:
\(\frac{1}{4+\sqrt{5}}\) యొక్క హారాన్ని అకరణీయం చేయండి.
జవాబు :
(a + √b) (a – √b) = a² – b అని మనకు తెలుసు. \(\frac{1}{4+\sqrt{5}}\) యొక్క లవహారాలను 4 – √5 తో గుణించగా

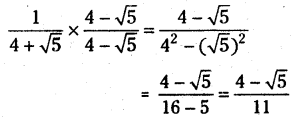
ఉదాహరణ – 18:
\(\frac{1}{7+4 \sqrt{3}}\) యొక్క హారాన్ని అకరణీయం చేయండి.
జవాబు :

ఉదాహరణ – 19:
\(\frac{1}{7+4 \sqrt{3}}+\frac{1}{2+\sqrt{5}}\)ను సూక్ష్మీకరించండి.
జవాబు :
7 + 4√3 యొక్క అకరణీయ కారణాంకం 7 – 4√3 మరియు 2 + √5 యొక్క అకరణీయ కారణాంకం 2 – √5.

= 7 – 4√3 – 2 + √5 = 5 – 4√5 + √5

ఉదాహరణ – 20:
సూక్ష్మీకరించండి.
(i) 2^2/3 . 2^1/3
జవాబు :
2^2/3 . 2^1/3 = 2^{\(\left(\frac{2}{3}+\frac{1}{3}\right)\)} = 2^3/2 = 2¹ = 2

(ii) (5^1/7)⁴
జవాబు :
(5^1/7)⁴ = 5^4/7

(iii) \(\frac{3^{\frac{1}{5}}}{3^{\frac{1}{3}}}\)
జవాబు :

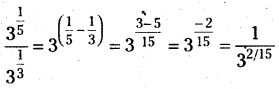
(iv) 7^1/17 . 11^1/17
జవాబు :
7^1/17 . 11^1/17 = (7 × 11)^1/17 = 77^1/17