AP Board 10th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు Ex 1.3

SCERT AP 10th Class Maths Textbook Solutions Chapter 1 పూర్ణ సంఖ్యలు Ex 1.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు Exercise 1.3

ప్రశ్న1.
కింది అకరణీయ సంఖ్యలను దశాంశ రూపంలో రాయండి. ఇందులో ఏవి అంతమయ్యే దశాంశాలో, ఏవి అంతంకాని ఆవర్తన దశాంశాలో తెలపండి.
(i) \(\frac{3}{8}\)

(ii) \(\frac{229}{400}\)

(iii) 4 \(\frac{1}{5}\)

(iv) \(\frac{2}{11}\)

(v) \(\frac{8}{125}\)
సాధన.
(i) \(\frac{3}{8}\)

\(\frac{3}{8}\) = 0.375 అంతమయ్యే దశాంశము.
(లేదా)
2వ పద్ధతి :
\(\frac{3}{8}=\frac{3}{2^{3}}=\frac{3 \times 5^{3}}{2^{3} \times 5^{3}}=\frac{3 \times 125}{(2 \times 5)^{3}}\) = \(\frac{375}{10^{3}}\) = 0.375
∴ \(\frac{3}{8}\) = 0.375 అంతమయ్యే దశాంశము.

(ii) \(\frac{229}{400}\)

∴ \(\frac{229}{400}\) = 0.5725 అంతమయ్యే దశాంశము.
400

(లేదా) 2వ పద్ధతి :
\(\frac{229}{400}=\frac{229}{2^{4} \times 5^{2}}=\frac{229 \times 5^{2}}{2^{4} \times 5^{4}}=\frac{5725}{10^{4}}\) = 0.5725
∴ \(\frac{229}{400}\) = 0.5725 అంతమయ్యే దశాంశము.

(iii) 4 \(\frac{1}{5}\)
4 \(\frac{1}{5}\) = \(\frac{21}{5}\) = 4.2 అంతమయ్యే దశాంశము.
(లేదా)

2వ పద్ధతి :
\(4 \frac{1}{5}=\frac{21}{5}=\frac{21 \times 2}{5 \times 2}=\frac{42}{10}\) = 4.2 అంతమయ్యే దశాంశము.

(iv) \(\frac{2}{11}\)

∴ \(\frac{2}{11}\) = 0.18181. …… = \(0 . \overline{18}\)
అంతంకాని ఆవర్తన దశాంశము.

(v) \(\frac{8}{125}\)

\(\frac{8}{125}\) = 0.064 అంతమయ్యే దశాంశము.

(లేదా)
2వ పద్ధతి :
\(\frac{8}{125}=\frac{8}{5^{3}}=\frac{8 \times 2^{3}}{5^{3} \times 2^{3}}=\frac{64}{(10)^{3}}\) = 0.064

∴ \(\frac{8}{125}\) = 0.064 అంతమయ్యే దశాంశము.

ప్రశ్న2.
భాగహార ప్రక్రియ లేకుండానే క్రింది అకరణీయ సంఖ్యలలో వేటిని అంతమయ్యే దశాంశాలుగా రాయగలమో, వేటిని అంతం కాని ఆవర్తన దశాంశాలుగా రాయగలమో తెలపండి.
(i) \(\frac{13}{3125}\)

(ii) \(\frac{11}{12}\)

(iii) \(\frac{64}{455}\)

(iv) \(\frac{15}{1600}\)

(v) \(\frac{29}{343}\)

(vi) \(\frac{23}{2^{3} 5^{2}}\)

(vii) \(\frac{129}{2^{2} 5^{7} 7^{5}}\)

(viii) \(\frac{9}{15}\)

(ix) \(\frac{36}{100}\)

(x) \(\frac{77}{210}\)
సాధన.
(i) \(\frac{13}{3125}\)

\(\frac{13}{3125}=\frac{13}{5^{5}}=\frac{13}{2^{0} \times 5^{5}}\)

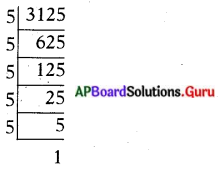
హారం (q) = 2ⁿ × 5^m రూపంలో కలదు.
∴ \(\frac{13}{3125}\) అంతమయ్యే దశాంశం.
.
(ii) \(\frac{11}{12}\)

\(\frac{11}{12}=\frac{11}{2^{2} \times 3}\)

హారం (q) = 2ⁿ × 5^m రూపంలో లేదు.
∴ \(\frac{11}{12}\) అంతంకాని ఆవర్తన దశాంశము.

(iii) \(\frac{64}{455}\)

\(\frac{15}{1600}=\frac{3 \times 5}{2^{6} \times 5^{2}}=\frac{3}{2^{6} \times 5^{1}}\)
హారం (q) = 2ⁿ × 5^m రూపంలో లేదు.
∴ \(\frac{64}{455}\) అంతంకాని ఆవర్తన దశాంశము.

(iv) \(\frac{15}{1600}\)

హారం (q) = 20 x 5m రూపంలో కలదు.
∴ \(\frac{15}{1600}\) అంతమయ్యే దశాంశము.

(v) \(\frac{29}{343}=\frac{29}{7^{3}}\)
హారం (q) = 2ⁿ × 5^m రూపంలో లేదు.
∴ \(\frac{29}{343}\) అంతంకాని ఆవర్తన దశాంశము.

(vi) \(\frac{23}{2^{3} \cdot 5^{2}}\)
హారం (q) = 2ⁿ × 5^m రూపంలో కలదు.
\(\frac{23}{2^{3} \cdot 5^{2}}\) అంతమయ్యే దశాంశము.

(vii) \(\frac{129}{2^{2} \cdot 5^{7} \cdot 7^{5}}\) అంతంకాని ఆవర్తన దశాంశము.
హారం (q) = 2ⁿ × 5^m రూపంలో లేదు.

(viii) \(\frac{9}{15}\)
\(\frac{9}{15}=\frac{3 \times 3}{3 \times 5}=\frac{3}{5}=\frac{3}{2^{0} \times 5^{1}}\)
హారం (q) = 2ⁿ × 5^m రూపంలో కలదు.
∴ \(\frac{9}{15}\) అంతమయ్యే దశాంశము.

(ix) \(\frac{36}{100}=\frac{2 \times 2 \times 3 \times 3}{10^{2}}\)
\(\frac{2^{2} \times 3^{2}}{2^{2} \times 5^{2}}=\frac{3^{2}}{5^{2}}=\frac{9}{2^{0} \times 5^{2}}\)
హారం (q) = 2ⁿ × 5^m రూపంలో కలదు.
∴ \(\frac{36}{100}\) అంతమయ్యే దశాంశము.

(x) \(\frac{77}{210}=\frac{7 \times 11}{2 \times 5 \times 7 \times 3}=\frac{11}{2 \times 5 \times 3}\)

హారం (q) = 2ⁿ × 5^m రూపంలో లేదు.
∴ \(\frac{77}{210}\) అంతం కాని ఆవర్తన దశాంశము.

ప్రశ్న3.
సిద్దాంతం 1.3 ను అనుసరించి కింది అకరణీయ సంఖ్యల యొక్క దశాంశ రూపాన్ని తెలపండి.
(i) \(\frac{13}{25}\)
(ii) \(\frac{15}{16}\)
(iii) \(\frac{23}{2^{3} \cdot 5^{2}}\)
(iv) \(\frac{7218}{3^{2} \cdot 5^{2}}\)
(v) \(\frac{143}{110}\)
సాదన.
(i) \(\frac{13}{25}\)
\(\frac{13}{25}=\frac{13}{5^{2}}=\frac{13 \times 2^{2}}{5^{2} \times 2^{2}}\)

= \(\frac{13 \times 4}{(5 \times 2)^{2}}=\frac{52}{10^{2}}\) = 0.52

(ii) \(\frac{15}{16}\)

\(\frac{15}{16}=\frac{3 \times 5}{2^{4}}=\frac{3 \times 5 \times 5^{4}}{2^{4} \times 5^{4}}=\frac{3 \times 5 \times 625}{(2 \times 5)^{4}}\)

= \(\frac{9375}{(10)^{4}}\) = 0.9375

(iii) \(\frac{23}{2^{3} \cdot 5^{2}}\)

\(\frac{23}{2^{3} \cdot 5^{2}}=\frac{23 \times 5}{2^{3} \cdot 5^{2} \times 5}=\frac{115}{2^{3} \times 5^{3}}=\frac{115}{10^{3}}\) = 0.115

(iv) \(\frac{7218}{3^{2} \cdot 5^{2}}\)

\(\frac{7218}{3^{2} \cdot 5^{2}}=\frac{2 \times 3^{2} \times 401}{3^{2} \times 5^{2}}=\frac{2 \times 401 \times 2^{2}}{5^{2} \times 2^{2}}\)

= \(\frac{2 \times 401 \times 4}{10^{2}}=\frac{3208}{10^{2}}\) = 32.08

(v) \(\frac{143}{110}\)
\(\frac{143}{110}=\frac{11 \times 13}{2 \times 5 \times 11}=\frac{13}{10}\) = 1.3

ప్రశ్న4.
కింద కొన్ని వాస్తవసంఖ్యల దశాంశరూపాలు ఇవ్వబడినవి. ప్రతి సందర్భంలోనూ ఇవ్వబడిన సంఖ్య అకరణీయమో, కాదో తెలపండి. ఆ సంఖ్య అకరణీయమై ఉండి \(\frac{p}{q}\) రూపంలో రాయగలిగితే q యొక్క ప్రధాన కారణాంకాలను గూర్చి నీవు ఏమి చెప్పగలవు ?
(i) 43.123456789
(ii) 0.120120012000120000…
(iii) \(43 . \overline{123456789}\)
సాధన.
(i) 43.123456789 అంతమయ్యే దశాంశము. కావున. అకరణీయము.
\(\frac{p}{q}\) రూపంలో రాయగలము.
q = 2ⁿ × 5^m రూపంలో ఉంటుంది.
m, n లు రుణేతర పూర్ణసంఖ్యలు.
q యొక్క ప్రధాన కారణాంకాలు 2 లేదా 5 లేదా 2, 5 లు.

(ii) 0.120120012000120000…….. అంతం
కావడం లేదు లేదా ఆవర్తనము కావడం లేదు:
కావున అకరణీయము కాదు.
∴ \(\frac{p}{q}\) రూపంలో రాయలేము.

(iii) \(43 . \overline{123456789}\) అంతంకాని ఆవర్తన – దశాంశము.
కావున అకరణీయ సంఖ్య.
∴ \(\frac{p}{q}\) రూపంలో రాయవచ్చును.
q = 2ⁿ x 5^m x 3^r x 7^s x 11^t ……. యొక్క ప్రధాన కారణాంకాలలో 2, 5 లు ఉండవు.
లేదా 2, 5లతో పాటు ఇతర ప్రధానకారణాంకాలు ఉంటాయి.