AP Board 10th Class Maths Solutions Chapter 1 వాస్తవ సంఖ్యలు InText Questions

SCERT AP 10th Class Maths Textbook Solutions Chapter 1 పూర్ణ సంఖ్యలు InText Questions Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 1st Lesson వాస్తవ సంఖ్యలు InText Questions

ఇవి చేయండి:

ప్రశ్న 1.
a = bq + r అయ్యే విధంగా ధనపూర్ణ సంఖ్యలు a మరియు b లకు అనుగుణంగా q మరియు r ల విలువలను కనుగొనుము. (పేజీ నెం. 3)
(i) a = 13, b = 3
(ii) a = 8, b = 80
(iii) a = 125, b = 5
(iv) a = 132, b= 11
సాధన.
(i) a = 13, b = 3

∴ 13 = 3(4) + 1
ఇది a = bq + r
రూపంలో ఉంది. ఇచ్చట q = 4, r = 1.2

(ii) a = 80, b = 8 అని తీసుకొనవలెను.

∴ 80 = 8(10) + 0 ను
a = bq + r తో పోల్చగా
q = 10; r = 0

iii) a = 125, b = 5

∴ 125 = 5(25) + 0 దీనిని 125
a = bq + r తో పోల్చగా .
q = 25; r = 0 అగును

(iv) a = 132, b = 11

∴ 132 = 11(12) + 0 దీనిని
132 a = bq + r తో పోల్చగా
q = 12; r = 0 అగును

ప్రశ్న 2.
యూక్లిడ్ భాగహార న్యాయాన్ని ఉపయోగించి క్రింది వాటి యొక్క గ.సా.భాను కనుగొనుము. (పేజీ నెం. 4)
(i) 50 మరియు 70
(ii) 96 మరియు 72
(iii) 300 మరియు 550
(iv) 1860 మరియు 2015
సాధన.
యూక్లిడ్ భాగహార న్యాయం ప్రకారం ఇచ్చిన సంఖ్యల యొక్క గ.సా.భా కనుగొనాలంటే (a, b) లకు వాటిని a = bq + r రూపంలో వ్రాసి ఆ తదుపరి b = rs + t మరియు r = tu + v … రూపంలో వ్రాసి చివరకు శేషం ‘0’ వచ్చునంత వరకు (అనగా K = LM + 0 రూపం వరకు) చేయాలి. అపుడు ‘L’ అనునది a, b ల యొక్క గ.సా.భా అగును.

i) 50 మరియు 70
a = 70, b = 50 వీటిని a = bq + r రూపంలో వ్రాయగా
70 = 50 (1) + 20
50 = 20(2) + 10
20 = 10 (2) + 0
∴ 50, 70 ల గ.సా.భా = 10

(ii) 96 మరియు 72 ఇచ్చట a = 96; b = 72 వీటిని
a = bq + r రూపంలో వ్రాయగా
96 = 72(1) + 24
72 = 24 (3) + 0
కావున 96, 72ల గ.సా.భా = 24

(iii) 300 మరియు 550; a = 550; b = 300
వీటిని a = bq + r రూపంలో వ్రాయగా
550 = 300 (1) + 250
300 = 250 (1) + 50
250 = 50(5) + 0
∴ 300, 550 ల గ.సా.భా = 50

(iv) 1860 మరియు 2015
a = 2015, b = 1860 వీటిని a = bq + r రూపంలో వ్రాయగా,
2015 = 1860(1) + 155
1860 = 155(12) + 0
కావున 2015, 1860 ల గ.సా.భా = 155

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
పై “ఇవి చేయండి’ లోని q మరియు / ల స్వభావం ఏమిటి ? (పేజీ నెం. 3)
సాధన.
ఇవి చేయండిలో ఇవ్వబడిన ప్రతి a, b విలువలకు p మరియు r పూర్ణాంకాలు మరియు ఏకైకాలు అనగా ప్రతి a, b విలువలకు a = bq + r అయ్యే విధంగా q, r లకు సంబంధించి ఒకే ఒక విలువ చొప్పున వ్యవస్థితమగును.

ప్రశ్న 2.
1.2 మరియు 0.12ల గ.సా.భాను మీరు కనుగొనగలరా? మీ జవాబును సమర్ధించండి. (పేజీ నెం. 4)
సాధన.
1.2 మరియు 0.12ల గ.సా.భా కనుగొనగలము. 1.2 = 0.12(10) + 0; 1.2, 0.12లు పూర్ణాంకాలు కానప్పటికి వాటి గ.సా.భాను భాగహార పద్దతిన కనుగొనవచ్చు.
ఉదా : 1.2లీ Pepsi bottle ను, 0.12లీ. మరొక చిన్న’ water bottle నింపుటకు తీసుకొనవలసిన మరొక కొలపాత్ర గరిష్ట ఘ||ప = దాని గ.సా.భాయే.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
యూక్లిడ్ భాగహార న్యాయంలోని a = bq + r లో r = 0 అయిన a, b మరియు q మధ్య సంబంధం ఏమిటి ? (పేజీ నెం. 6)
సాధన.
a = bq + r నందు r = 0 అయిన a = bq అగును. అనగా \(\frac{a}{b}\) = q. అంటే ‘a’ ని ప నిశ్శేషంగా భాగిస్తుందని అర్థం.
∴ ‘a’ కు b ఒక కారణాంకం మరియు q కూడా మరొక కారణాంకం అగును.

ఇవి చేయండి:

ప్రశ్న 1.
2310 ను ప్రధాన కారణాంకాల లబ్దంగా రాయండి. ఈ సంఖ్యను నీ స్నేహితులు ఏవిధంగా కారణాంకాల లబ్ధంగా రాశారో చూడండి. నీవు చేసినట్లుగానే వారు కూడా చేశారా? చివరి ఫలితాన్ని, నీ స్నేహితుల ఫలితంతో సరిచూడుము. దీని కొరకు 3 లేదా 4 సంఖ్యలను తీసుకొని ప్రయత్నించుము. నీవు ఏమి గమనిస్తావు ? (పేజీ నెం. 7)
సాధన.

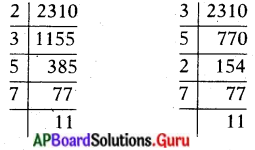
2310 = 2 × 3 × 5 × 7 × 11
2310 = 3 × 5 × 2 × 7 × 11

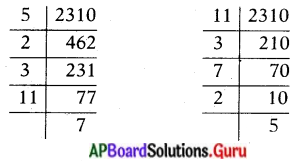
2310 = 5 × 2 × 3 × 11 × 7
2310 = 11 × 3 × 7 × 2 × 5
2310 ని వేర్వేరు విధాలుగా ప్రధాన కారణాంకాల లబంగా రాసినప్పుడు ప్రధాన కారణాంకాల క్రమం మారిందే కాని ప్రధాన కారణాంకాలు మారలేదు. అనగా 2310ని ప్రధాన కారణాంకాల లంగా ఒకే విధంగా రాయవచ్చును.

ప్రశ్న 2.
ఇవ్వబడిన సంఖ్యల జతల యొక్క క.సా.గు మరియు గ.సా.భా లను ప్రధాన కారణాంక పద్ధతి ఆధారంగా కనుగొనుము. (పేజీ నెం. 8)
(i) 120, 90
(ii) 50, 60
(iii) 37, 49
సాధన.
(i) 120, 90
120, 90 వీటిని ప్రధాన కారణాంకాల లబ్ధ పద్ధతిలో వ్రాయగా
120 = 2 × 2 × 2 × 3 × 5 = 2³ × 3¹ × 5¹
90 = 2 × 3 × 3 × 5 = 2¹ × 3² × 5¹
గ.సా.కా = ఉమ్మడి (సామాన్య) కారణాంకాల కనిష్ఠ ఘాతాల లబ్దం
∴ 120, 90 లలో గల ఉమ్మడి ప్రధాన కారణాంకాలు = 2, 3, 5
2, 3, 5 లలో కనిష్ఠ ఘాతాలు = 2¹, 3¹, 5¹
∴ గ.సా.కా = 2 × 3 × 5 = 30
120, 90 ల గ.సా.కా = 30
క.సా.గు = అన్ని ప్రధాన కారణాంకాల గరిష్ఠ ఘాతాల లబ్దం 120, 90 లలో గల అన్ని ప్రధాన కారణాంకాలు = 2, 3, 5
2, 3, 5 ల గరిష్ఠ ఘాతాలు = 2³, 3², 5¹ .
∴ 120, 90 ల క.సా.గు = 2³ × 3² × 5¹
= 8 × 9 × 5 = 360
120, 90 ల క.సా.గు = 360.

(ii) 50, 60
50, 60 వీటిని ప్రధాన కారకాలు లజ్జ పద్దతిలో వ్రాయగా
50 = 2 × 5 × 5 = 2¹ × 5² = [2¹] × 5²
60 = 2 × 2 × 3 × 5 = 2² × 3¹ × [5¹]
50, 60 లలో గల ఉమ్మడి ప్రధాన కారణాంకాలు = 2, 5 2, 3 ల యొక్క కనిష్ఠ ఘాతాంకాల లబ్దం = 2 × 5 = 10
∴ 50, 60 ల గ.సా.కా = 10
50, 60 లలో గల అన్ని ప్రధాన కారణాంకాలు = 2, 3, 5
2, 3, 5ల ఘాతాలలో గరిష్ఠ ఘాతాలు = 2², 3, 5²
∴ 2, 3, 5 ల గరిష్ఠ ఘాతాల-లబ్ధం = 2² × 3 × 5² = 300
∴ 50, 60 ల క.సా.గు = వాటి యొక్క అన్ని ప్రధాన కారణాంకాల గరిష్ఠ ఘాతాల లబ్దం = 300.

(iii) 37, 49
37, 49 లను ప్రధాన కారణాంకాల లబ్ధ పద్ధతిలో వ్రాయగా
37 = 37 × 1; 49 = 7² × 1
37, 49 లలో గల సామాన్య కారణాంకం = 1
∴ 1 యొక్క కనిష్ఠ ఘాతాంకం కూడా ఒకటే కావున 37, 49ల గ.సా. కా = 1 మరియు
37, 49ల యొక్క అన్ని ప్రధాన కారణాంకాలు = 37, 1, 7
37, 1, 7 ల యొక్క గరిష్ట ఘాతాలు = 37¹, 1¹, 7²
∴ 37, 7 ల యొక్క గరిష్ఠ ఘాతాల లబ్ధం = 37 × 7² = 1813
∴ 37, 49 ల క.సా.గు = 1813.

ప్రయత్నించండి:

ప్రశ్న 1.
‘n’ మరియు ‘m’ ఏవేని సహజ సంఖ్యలకు 3ⁿ × 4^m యొక్క ఫలిత సంఖ్య ) లేదా 5 తో అంతం కాదని చూపుము. (పేజీ నెం. 8)
సాధన.
3ⁿ × 4^m = 3ⁿ × (2²)^m
= 3ⁿ × 2^2m a
= 3ⁿ × 2^m × 2^m
అనగా పై లబ్దంలో 2, మరియు 3 అనే ప్రధాన కారణాంకాలు మాత్రమే గలవు. కాని ఒక సంఖ్య ‘0’ లేదా ‘5’ తో అంతం కావలెనన్న దాని ప్రధాన కారణాంకాలలో 5 ఖచ్చితంగా ఉండాలి.
కాని 3ⁿ × 4^m ఫలిత సంఖ్య యొక్క ప్రధాన కారణాంకాలలో 5 లేదు. కావున దాని ఫలిత సంఖ్య ‘0’ లేదా ‘5’ తో అంతం కాదు.

ఇవి చేయండి:

ప్రశ్న 1.
కింది అంతమొందే దశాంశాలను అకరణీయ సంఖ్యలుగా (\(\frac{p}{q}\), q# 0 మరియు p, q లు సాపేక్ష ప్రధానాంకాలు) రాయండి. (పేజీ నెం. 10)
(i) 15.265
(ii) 0.1255
(iii) 0.4
(iv) 23.34
(v) 1215.8
సాధన.
(i) 15.265 = \(\frac{15265}{10^{3}}=\frac{5 \times 43 \times 71}{2^{3} \times 5^{3}}\)
= \(\frac{3053}{200}\)

(ii) 0.1255 = \(\frac{1255}{10^{4}}=\frac{5 \times 251}{2^{4} \times 5^{4}}=\frac{251}{2000}\)

(iii) 0.4 = \(\frac{4}{10}=\frac{2 \times 2}{5 \times 2}=\frac{2}{5}\)

(iv) 23.34 = \(\frac{2334}{10^{2}}=\frac{2 \times 3 \times 389}{2^{2} \times 5^{2}}\)
= \(\frac{1167}{50}\)

v) 1215.8 = \(\frac{12158}{10}=\frac{2 \times 6079}{2 \times 5}\)
= \(\frac{6079}{5}\)

ప్రశ్న 2.
కింది అకరణీయ సంఖ్యలు P రూపంలో ఉన్నాయి. ఇందులో q యొక్క రూపం 2ⁿ5^m మరియు ఇందులో n, m లు రుణేతర పూర్ణ సంఖ్యలు అయిన వీటిని దశాంశ రూపాలలోనికి మార్చండి. (పేజీ నెం. 11)
సాధన.
(i) \(\frac{3}{4}\)
= \(\frac{3}{4}=\frac{3}{2^{2}}=\frac{3 \times 5^{2}}{2^{2} \times 5^{2}}=\frac{3 \times 25}{(10)^{2}}=\frac{75}{100}\) = 0.75

(ii) \(\frac{7}{25}\)
\(\frac{7}{25}=\frac{7}{5^{2}}=\frac{7 \times 2^{2}}{5^{2} \times 2^{2}}=\frac{28}{100}\) = 0.28

(iii) \(\frac{51}{64}\)
\(\frac{51}{64}=\frac{3 \times 17}{2^{6}}=\frac{3 \times 17 \times 5^{6}}{2^{6} \times 5^{6}}=\frac{796875}{10^{6}}\) = 0.796875

(iv) \(\frac{14}{25}\)
= \(\frac{14}{5^{2}}=\frac{14 \times 2^{2}}{5^{2} \times 2^{2}}=\frac{14 \times 4}{10^{2}}\)
= \(\frac{56}{100}\) = 0.56

(v) \(\frac{80}{100}\)
= \(\frac{80}{2^{2} \times 5^{2}}\)
= 0.80 = 0.8

ప్రశ్న 3.
కింది అకరణీయ సంఖ్యలను దశాంశాలుగా రాయండి. భాగఫలంలో ఆవర్తనం చెందే అంకెల సమూహాన్ని కనుగొనండి. (పేజీ నెం. 11)
(i) \(\frac{1}{3}\)
(ii) \(\frac{2}{7}\)
(iii) \(\frac{5}{11}\)
(iv) \(\frac{10}{13}\)
సాధన.
(i) \(\frac{1}{3}\)
\(\frac{1}{3}\) = 0.3333 …….. = \(0 . \overline{3}\)
భాగఫలంలో ఆవర్తనం చెందే అంకెల సమూహం = 3.

(ii) \(\frac{2}{7}\)

\(\frac{2}{7}\) = 0.285714285 …..
ఆవర్తనం చెందే అంకెల సమూహం = 285714

(iii) \(\frac{5}{11}\)

\(\frac{5}{11}\) = 0.454545…
ఆవర్తనం చెందే అంకెల సమూహం = 45

iv) \(\frac{10}{13}\)

\(\frac{10}{13}\) = \(0 . \overline{769230}\)
ఆవర్తనం చెందే అంకెల సమూహం = 769230

ప్రవచనం:

ప్రశ్న 1.
p అనేది ఒక ప్రధానసంఖ్య మరియు a ఒక ధన పూర్ణ సంఖ్య అయితే “a² ను p నిశ్శేషంగా భాగిస్తే : ను p నిశ్శేషంగా” భాగిస్తుంది. (పేజీ నెం. 13)
నిరూపణ :
‘a’ అనేది ఒక ధన పూర్ణ సంఖ్య అయితే ఈ యొక్క ప్రధాన కారణాంకాల లబ్ధంను క్రింది విధంగా రాయవచ్చును.
a = p₁, p₂, …. , P_n, ఇందులో p₁, p₂, ….., p_n లు ప్రధానాంకాలు మరియు వేర్వేరుగా ఉండనవసరం లేదు.
అందుచే a² = (p₁, p₂., ….. P_n) (p₁ P₂, …………… P_n) = p₁², p₂²……….p_n². a² ను p నిశ్శేషంగా భాగించునని ఇవ్వబడినందున అంకగణిత ప్రాథమిక సిద్ధాంతంను అనుసరించి a² యొక్క ఒక ప్రధాన కారణాంకాల, లబ్ధం p₁, p₂, ….., p_n అగును. కావున p అనేది p₁, p₂, ….. P_n లలో ఒకటిగా వుంటుంది. ఇప్పుడు p₁, p₂, ……. P_n లలో p ఒకటిగా ఉన్నందున, p, a ను కూడా నిశ్శేషంగా భాగిస్తుంది.

ఇవి చేయండి:

ప్రశ్న 1.
p = 2, p = 5 మరియు a² = 1, 4, 9, 25, 36, 49, 64 మరియు 81 అయిన పైన నిరూపించిన ‘ ప్రవచనంను ఈ విలువలకు సరిచూడండి. (పేజీ నెం. 14)
సాధన.
p = 2 తీసుకొందాం.
i) a² = 1 అయిన a = 1
a² = 1 ని p = 2 నిశ్శేషంగా భాగించదు.
a = 1 ని p = 2 నిశ్శేషంగా భాగించదు.

(ii) a² = 4 అయిన a = 2
a² = 4 ని p = 2 నిశ్శేషంగా భాగిస్తుంది.
a = 2 ని p = 2 నిశ్శేషంగా భాగిస్తుంది.

(iii) a² = 9 అయిన a = 3
a² = 9 ని p = 2 నిశ్శేషంగా భాగించదు.
a = 3 ని p = 2 నిశ్శేషంగా భాగించదు.

(iv) a² = 25 అయిన a = 5
a² = 25 ని p = 2 నిశ్శేషంగా భాగించదు.
a = 5ని p = 2 నిశ్శేషంగా భాగించదు.

(v) a² = 36 అయిన a = 6
a² = 36 ని p = 2 నిశ్శేషంగా భాగిస్తుంది.
a = 6 ని p = 2 నిశ్శేషంగా భాగిస్తుంది.

(vi) a² = 49 అయిన a = 1
a² = 49 ని p = 2 నిశ్శేషంగా భాగించదు.
a = 7 ని p = 2 నిశ్శేషంగా భాగించదు.

(vii) a² = 64 అయిన a = 8
a² = 64 ని p = 2 నిశ్శేషంగా భాగిస్తుంది.
a = 8 ని p = 2 నిశ్శేషంగా భాగిస్తుంది.

(viii) a² = 81 అయిన a = 9
a² = 81 ని p = 2 నిశ్శేషంగా భాగించదు.
a = 9 ని p = 2 నిశ్శేషంగా భాగించదు.

p = 5 తీసుకొందాం a² విలువ 1, 4, 9, 36, 49, 64, 81 అయినప్పుడు a² ను p = 5 నిశ్శేషంగా భాగించదు. మరియు aను కూడా p = 5 నిశ్శేషంగా భాగించదు.

a² = 25 అయినప్పుడు a² ను p = 5 నిశ్శేషంగా భాగిస్తుంది మరియు a = 5 ను కూడా p = 5 నిశ్శేషంగా భాగిస్తుంది.

ఆలోచించి, చర్చించి, రాయండి:

ప్రశ్న 1.
y = a^x లో y, a మరియు X ల స్వభావమేమిటి ? y యొక్క విలువ ఇచ్చినప్పుడు దాని అనురూప x విలువను ఎల్లప్పుడూ కనుగొనగలమా ? మీ సమాధానాన్ని సమర్థించండి. (పేజీ నెం. 17)
సాధన.
y = a^x నందు y విలువ ఎల్లప్పుడూ ధనాత్మకమే.
X విలువ ‘0’ అయిన y విలువ 1 అగును.
x విలువ ధనాత్మకమైన y విలువ 1 లేదా అంతకంటే ఎక్కువుండును.
x విలువ రుణాత్మకమైన y విలువ 1 కంటే తక్కువుండును. కాని ‘0’ కంటే ఎక్కువుండును.
y విలువ ఇచ్చినపుడు దాని అనురూప x – విలువను సూటిగా ఎల్లపుడూ సూటిగా కనుగొనలేము. గ్రాఫ్ సహాయంతో
రమారమి (సుమారు) విలువను కనుగొనవచ్చును.

ప్రశ్న 2.
2¹ = 2, 4¹ = 4, 8¹ = 8 మరియు 10¹ = 10 అని మీకు తెలుసు. వీటి నుండి log₂ 2, log₄ 4, log₈ 8 మరియు log₁₀ 10 విలువలు ఏమై ఉంటాయి ? దీని నుండి మీరు ఏమి సాధారణీకరణం చేస్తారు ? (పేజీ నెం. 18)
సాధన.
a^x = N అయితే log_a N = X అని తెలుసు,
2¹ = 2 ను సంవర్తమాన రూపంలో వ్రాయగా log₂ 2 = 1 4
4¹ = 4 ను సంవర్గమాన రూపంలో వ్రాయగా log₄ 4 = 1
8¹ = 8 ను సంవర్గమాన రూపంలో వ్రాయగా log₈ 8 =1
10¹ = 10 ను సంవర్తమాన రూపంలో వ్రాయగా log₁₀ 10 = 1
అనగా ఏదైనా ఒకటి కంటే పెద్దదైన సహజ సంఖ్య యొక్క సంవర్గమాన విలువ (అదే భూమికి) 1 అగును. దీనిని సూత్రీకరించి log_a a = 1 గా సాధారణీకరిస్తాం.

ప్రశ్న 3.
log₁₀0 వ్యవస్థితం అవుతుందా ? (పేజీ నెం. 18)
సాధన.
log₁₀ 0 వ్యవస్థితం కాదు. ఎందుకనగా a^x = 0 అయ్యేటట్లు (a > 1) x విలువ వ్యవస్థితం కాదు కావున log₁₀ 0 వ్యవస్థితం కాదు. కావున సంవర్గమానాలు అనేవి కేవలం ధన వాస్తవ సంఖ్యలకు మాత్రమే పరిమితం చేస్తాం.

ప్రశ్న4.
7 = 2^x అయితే x = log₂ 7 అని మనకు తెలుసు. అయితే 2^{log₂ 7} యొక్క విలువ ఎంత ? మీ సమాధానాన్ని మరికొన్ని ఉదాహరణలతో సమర్ధించండి. (పేజీ నెం. 21) పై దాని నుండి a^{log_a N} ను ఏ విధంగా సాధారణీకరిస్తారు?
సాధన.
7 = 2^x అయిన x = log₂ 7 = log₂ 7
x = log₂ 7 విలువను 2″ నందు ప్రతిక్షేపించగా 2^x = 2^{log₂ 7} = 7 (దత్తాంశము నుండి)
7 = 2^x అయిన 2^{log₂ 7} = 7 అగును.
ఉదా :
(1) 5 = 3^y అయితే y = log₃ 5 అయిన 3^{log₃ 5} విలువ ఎంత ?
5 = 3^y
∴ సంవర్తమాన రూపం ప్రకారం y = log₃ 5 ఈ విలువను 3^y = 5 నందు ప్రతిక్షేపించగా 3^{log₃ 5} = 5

(2) 10 = 9^x అయిన x = log₉ 10 అయిన 9^{log₉ 10} విలువ ఎంత?
9^x = 10 (దత్తాంశం) దీని యందు x విలువ ప్రతిక్షేపిద్దాం 9^{log₉ 10} = 10 అయితే 9^{log₉ 10} = 10 అగును. పైదాని నుండి a^x = N అయిన log_a N = X అగును
∴ alog_a N = N అగును b^{log_b M} = M గా సాధారణీకరిస్తాం.

ఇవి చేయండి:

ప్రశ్న 1.
కింది సమీకరణాలలోని భూములను ఏ ఘాతాంకాలకు పెంచాలో రాయండి. (పేజీ నెం. 18)
(i) 7 = 2^x
(ii) 10 = 5^b
(iii) \(\frac{1}{81}\) = 3^c
(iv) 100 = 10^z
(v) \(\frac{1}{257}\) = 4^a
సాధన.
(i) 7 = 2^x
7 = 2^x నందు
x = 0 అయిన 2^x = 1 అగును
x = 1 అయిన 2^x = 2 అగును
x = 2 అయిన 2^x = 4 అగును
x = 3 అయిన 2^x = 8 అగును
అనగా x విలువ 2 పైబడి 3కు దగ్గరగా ఉండును. కాని ‘X’ యొక్క ఖచ్చిత విలువను నిర్ధారించలేము. అయితే పై (x, 2^x) విలువలను గ్రాఫ్ పై గుర్తించి 2^x = 7 అగునట్లు x విలువ ఉజ్జాయింపుగా తెలుసుకోవచ్చును.

(ii) 10 = 5^b నందు
b = 0 అయిన 5^b = 1 అగును. అదేవిధంగా
b = 1 అయిన 5^b = 5 అగును మరియు
b = 2 అయిన 5^b = 25 అగును.
కావునా 5^b = 10 అగునట్లు ‘b’ యొక్క ఖచ్చిత విలువను నిర్ధారించలేము.

(iii) \(\frac{1}{81}\) = 3^c నందు
c = 0 అయిన 3^c = 1 మరియు
c = – 2 అయిన 3^c = \(\frac{1}{9}\) మరియు
c = – 3 అయిన 3^c = \(\frac{1}{27}\) మరియు
c = – 4 అయిన 3^c = \(\frac{1}{81}\) అగును.
\(\frac{1}{81}\) = 3^c అనగా c = – 4 కావలెను.

(iv) 100 = 10^z నందు
z = 0 అయిన 10^z = 1
z = 1 అయిన 10^z = 10 అగును
z = 2 అయిన 10^z = 100 అగును
100 అగునట్లు 10^z నందు z = 2 గా తీసుకోవలెను.

(v) \(\frac{1}{257}\) = 4^a
a = 0 అయిన 4^a = 1
a = – 1 అయిన 4^a = \(\frac{1}{4}\)
a = – 2 అయిన 4^a = \(\frac{1}{16}\)
a = – 3 అయిన 4^a = \(\frac{1}{64}\)
a = – 4 అయిన 4^a = \(\frac{1}{256}\) అగును.
కాని \(\frac{1}{257}\) అగునట్లు ‘a’ విలువను ఖచ్చితంగా నిర్ధారించలేము.

ప్రశ్న 2.
కింది లబ్దాల సంవర్గమానాలను రెండు సంస్థమానాల. మొత్తంగా రాయండి. (పేజీ నెం. 19)
(i) 35 × 46
(ii) 235 × 437
(iii) 2437 × 3568
సాధన.
(i) 35 × 46 సూత్రం
log_a mn = log_a m + log_a n ప్రకారం
log (35 × 46) = log 35 + log 46
(ఏ ఆధారానికైనా)

(ii) 235 × 437
log (235 × 437) = log 235 + log 437

(iii) 2437 × 3568
log (2437 × 3568)
= log (2437) + log (3568)

ప్రశ్న 3.
కింది వాటి సంవర్గమానాలను రెండు సంవర్గమానాల భేదంగా రాయండి. (పేజీ నెం. 20)
(i) \(\frac{23}{34}\)
(ii) \(\frac{373}{275}\)
(iii) 4525 ÷ 3734
(iv) 5055 ÷ 3303
సాధన.
(i) \(\frac{23}{34}\) [log_a m= log_a m – log_a n]
log \(\frac{23}{34}\) = log 23 – log 34

(ii) log \(\frac{373}{275}\) = log 373 – log 275
(ఏ ఆధారానికైనా)

(iii) log \(\frac{4525}{3734}\) = log 4525 – log 3734

iv) log \(\frac{5055}{3303}\) = log 5055 – log 3303

ప్రశ్న 4.
log_a xⁿ = n log_a x ను ఉపయోగించి కింది ఘాతసంఖ్యల సంవర్గమానాలను మార్చి రాయండి. (పేజీ నెం. 21)
(i) log₂ 7²⁵
(ii) log₅ 8⁵⁰
(iii) log 5²³
(iv) log 1024
సాధన.
(i) log₂ 7²⁵ = 25 log₂ 7
(ii) log₅ 8⁵⁰= 50 log₅ 8
(iii) log 5²³ = 23 log 5
(iv) log 1024 = log 2¹⁰ = 10 log 2

ప్రయత్నించండి:

ప్రశ్న 1.
కింది వాటిని ఘాతరూపంలో వ్రాసి తద్వారా చరరాశులను నిర్ణయించండి. (పేజీ నెం. 18)
(i) log₂ 32 = x
(ii) log₅ 625 = y
(iii) log₁₀ 10000 = z
iv) log₇ \(\frac{1}{343}\) = – a
సాధన.
సూత్రం : log_a N = x యొక్క ఘాతరూపం a^x = N అగును.

(i) log₂ 32 = x యొక్క ఘాతరూపం 2^x = 32 = 2⁵
∴ x = 5

(ii) log₅ 625 = y యొక్క ఘాతరూపం 5^y = 625 = 5⁴
∴ 5^y = 5⁴
⇒ y = 4

(iii) log₁₀ 10000 = z యొక్క ఘాతరూపం
10^z = 10000 = 10⁴
10^z = 10⁴
⇒ z = 4

iv) log₇ = – a యొక్క ఘాతరూపం
7^{– a} = \(\frac{1}{343}\)
7^{– a} = \(\frac{1}{7^{a}}=\frac{1}{343}=\frac{1}{7^{3}}\)
∴ \(\frac{1}{7^{\mathrm{a}}}=\frac{1}{7^{3}}\)
⇒ a = 3 అగును.

ప్రశ్న 2.
కింది వాటి విలువలను కనుగొనండి. (పేజీ నెం. 21)
(i) log₂ 32
(ii) log_c √c
(iii) log₁₀ 0.001
(iv) \(\log _{\frac{2}{3}} \frac{8}{27}\)
సాధన.
(i) log₂ 32 = log₂ 2
= 5 log₂ 2
= 5(1) = 5

(ii) log_c √c = log_c c^{\(\frac{1}{2}\)}
= \(\frac{1}{2}\) log_c c
= \(\frac{1}{2}\) (1) = \(\frac{1}{2}\)

(iii) log₁₀ 0.001 = log₁₀ \(\frac{1}{1000}\)
= log₁₀ 10^-3
= – 3 log₁₀ 10
= – 3(1) = – 3.

(iv) \(\log _{\frac{2}{3}} \frac{8}{27}\) = \(\log _{\frac{2}{3}}\left(\frac{2}{3}\right)^{3}\)
= \(3 \log _{\frac{2}{3}} \frac{2}{3}\) = 3(1) = 3.

ఉదాహరణలు:

ప్రశ్న 1.
q ఏదైనా ఒక పూర్ణసంఖ్య అయినప్పుడు, ప్రతి ధన సరి పూర్ణ సంఖ్య 2q రూపంలో మరియు ప్రతి ధన బేసి పూర్ణ సంఖ్య 24 + 1 రూపంలో ఉంటుందని చూపుము. (పేజీ నెం. 5)
సాధన.
a ఒక ధనపూర్ణ సంఖ్య మరియు b = 2 అనుకుందాం.
అపుడు a = 2q + r (భాగహార న్యాయం ప్రకారం)
∴ ప్రతీ పూర్ణసంఖ్య q ≥ 0 కు r విలువ 0 లేదా 1 అవుతుంది. ఎందుకనగా 0 ≤ r < 2 కావున a = 2q + 0 లేదా a = 2q + 1 అగును.
‘a’ అనేది 2q + 0 రూపంలో ఉంటే అది సరి పూర్ణ సంఖ్య అగును.
a అనేది 2q + 1 రూపంలో ఉంటే అది సరి పూర్ణసంఖ్య కాదు. కావున ఖచ్చితంగా అపుడు బేసి సంఖ్య అగును. కావున ప్రతీ బేసి సంఖ్య a = 2q + 1 రూపంలో ఉండును.

ప్రశ్న 2.
q ఏదైనా ఒక పూర్ణ సంఖ్య అయినప్పుడు, ప్రతి ధన బేసి సంఖ్య 4q + 1 లేదా 4q + 3 రూపంలో ఉంటుందని చూపుము. (పేజీ నెం. 5)
సాధన.
a ఏదైనా ఒక ధన బేసి పూర్ణసంఖ్య అనుకుందాం. a మరియు b = 4 పై యూక్లిడ్ భాగహార శేష విధిని అనువర్తింపజేయగా 0 ≤ r < 4 కావున శేషం ‘0’ లేదా ‘1’ లేదా ‘2’ లేదా ‘3’ అవుతాయి. వీటి ఆధారంగా ‘a’ యొక్క ‘విలువలు 4q + 0 లేదా 4q + 1 లేదా 4q + 2 లేదా 4q + 3 కావచ్చును. వీటిలో 4q, 4q + 2 లు , ‘2’ చే నిశ్శేషంగా భాగింపబడును. కావున అవి సరిసంఖ్యలు అనగా అవి బేసి సంఖ్యలు కానేరవు.
∴ అందువల్ల బేసి సంఖ్య ‘a’ యొక్క రూపం = 4q + 1 లేదా 4q + 3 అగును.

ప్రశ్న 3.
n ఒక సహజసంఖ్యగా గల సంఖ్య 4ⁿ తీసుకోండి. n యొక్క ఏ విలువకైనా 4ⁿ విలువ గల సంఖ్య “సున్న’ అంకెతో అంతమౌతుందో, లేదో సరిచూడండి. (పేజీ నెం. 7)
సాధన.
n సహజసంఖ్యగా గల సంఖ్య 4ⁿ విలువగల సంఖ్య సున్నతో అంతం కావాలంటే అది ‘5’ చే నిశ్శేషంగా భాగించబడాలి. అంటే 4ⁿ సంఖ్య యొక్క ప్రధాన కారణాంకాల లబ్ధంలో 5 ఒక ప్రధాన సంఖ్యగా ఉండాలి. కాని ఇది సాధ్యం కాదు. ఎందువలన అనగా 4ⁿ = (2)²ⁿ. అందుచే 4ⁿ యొక్క ప్రధాన కారణాంకాల లబ్దంలో లేనందున, n ఏ సహజ సంఖ్య విలువకైననూ 4ⁿ అనే సంఖ్య ‘సున్న’తో అంతముకానేరదు.

ప్రశ్న 4.
12 మరియు 18ల యొక్క ర… మను క.సా.గులను ప్రధాన కారణ వస్తు ” పద్దు ” కనుగొనుము. (పేజీ నెల. 7)
సాధన.
12, 18 లను ప్రధాన కారణాంకాల లబ్ధ పద్ధతిలో విడదీయగా
12 = 2 × 2 × 3 = 2² × 3¹
18 = 2 × 3 × 3 = 2¹ × 3² అగును.
గ.సా.కా అనగా ఇచ్చిన సంఖ్యల యొక్క సామాన్య ప్రధాన కారణాంకాల కనిష్ఠ ఘాతాల లబ్ధం.
∴ 12, 18 ల యందు గల సామాన్య ప్రధాన కారణాంకాలు = 2, 3
∴ 12, 18 లలో 2, 3 ల యొక్క కనిష్ఠ ఘాతాలు _ = 2¹, 3¹
∴ 12, 18 ల గ.సా.కా = వాటి కనిష్ఠ ఘాతాల • లబ్ధం = 2¹ x 3¹ = 6
అదే విధంగా క.సా.గు అనగా –
ఇచ్చిన సంఖ్యల యొక్క ప్రధాన కారణాంకాలన్నింటి యొక్క గరిష్ఠ ఘాతాల లబ్దం.
12, 18 ల యొక్క అన్ని ప్రధాన కారణాంకాలు = 2, 3
12, 18 లలో 2, 3 ల యొక్క గరిష్ఠ ఘాతాలు = 2², 3²
12, 18 ల క.సా.గు = గరిష్ఠ ఘాతాల లబ్దం .. = 2² × 3² = 4 × 9 = 36.

ప్రశ్న 5.
నిర్వచింపబడిన సిద్ధాంతాల ఆధారంగా, భాగహారం చేయకుండానే క్రింది అకరణీయ సంఖ్యలు అంతమయ్యే దశాంశాలో, అంతం కాని ఆవర్తన దశాంశాలో తెలపండి. (పేజీ నెం. 12)
(i) \(\frac{16}{125}\)
(ii) \(\frac{25}{32}\)
(iii) \(\frac{100}{81}\)
(iv) \(\frac{41}{75}\)
సాధన.
\(\frac{16}{125}=\frac{16}{5 \times 5 \times 5}=\frac{16}{5^{3}}\)
(అంతమయ్యే దశాంశం)

(ii) \(\frac{25}{32}=\frac{25}{2 \times 2 \times 2 \times 2 \times 2}=\frac{25}{2^{5}}\)
(అంతమయ్యే దశాంశం)

(iii) \(\frac{100}{81}=\frac{100}{3 \times 3 \times 3 \times 3}=\frac{100}{3^{4}}\)
(అంతం కాని ఆవర్తన దశాంశం)

iv) \(\frac{41}{75}=\frac{41}{3 \times 5 \times 5}=\frac{41}{3 \times 5^{2}}\)
(అంతం కాని ఆవర్తన దశాంశం)

ప్రశ్న 6.
కింది అకరణీయ సంఖ్యలను భాగహారం చేయకుండానే దశాంశ రూపంలో రాయండి. (పేజీ నెం. 12)
(i) \(\frac{35}{50}\)
(ii) \(\frac{21}{25}\)
(iii) \(\frac{7}{8}\)
సాధన.
(i) \(\frac{35}{50}\)
= \(\frac{7 \times 5}{2 \times 5 \times 5}=\frac{7}{2 \times 5}=\frac{7}{10^{1}}\) = 0.7

(ii) \(\frac{21}{25}\)
= \(\frac{21}{5 \times 5}=\frac{21 \times 2^{2}}{5 \times 5 \times 2^{2}}\)
= \(\frac{21 \times 4}{5^{2} \times 2^{2}}=\frac{84}{10^{2}}\) = 0.84

(iii) \(\frac{7}{8}\)
= \(\frac{7}{2 \times 2 \times 2}=\frac{7}{2^{3}}=\frac{7 \times 5^{3}}{\left(2^{3} \times 5^{3}\right)}\)
= \(\frac{7 \times 125}{(2 \times 5)^{3}}=\frac{875}{(10)^{3}}\) = 0.875

ప్రశ్న 7.
√2 ను కరణీయ సంఖ్య అని నిరూపించండి. (పేజీ నెం. 14)
సాధన.
ఈ నిరూపణ ‘విరోధాభాసం’ (పరోక్ష పద్దతి) ద్వారా చేయుచున్నందున మనం నిరూపించవలసిన ఫలితానికి విరుద్ధంగా √2 అనేది ఒక అకరణీయ సంఖ్య అని భావిద్దాం .

ఇది అకరణీయం అయితే, r మరియు S అనే రెండు పూర్ణ సంఖ్యలు (s ≠ 0) √2 = \(\frac{a}{b}\) అయ్యేటట్లు వ్యవస్థితం అవుతుంది.

ఒకవేళ r మరియు S లకు 1 కాకుండా ఏదైనా సామాన్య కారణాంకం ఉంటే, ఆ సామాన్య కారణాంకం చేత భాగిస్తే మనకు √2 = \(\frac{a}{b}\), ఇందులో a మరియు b లు పరస్పర ప్రధానాంకాలుగా వస్తుంది. దీని నుండి b√2 = a అవుతుంది.

ఇరువైపులా వర్గం చేసి, క్రమంలో అమర్చగా, మనకు 2b² = a² వస్తుంది. అంటే a² ను 2 భాగిస్తుంది.

ఇప్పుడు ప్రవచనం – 1ను బట్టి a² ను 2 భాగించినందున a ను కూడా ఇది భాగిస్తుంది. అందుచే, మనం తిరిగి a = 2c, c అనేది ఒక పూర్ణసంఖ్యగా రాయవచ్చు. ఇందులో ‘a’ విలువను ప్రతిక్షేపించగా, మనకు 2b² = 4c² అంటే b² = 2c² వస్తుంది. అంటే b² ను 2 భాగిస్తుంది మరియు bని 2 భాగిస్తుంది. (ప్రవచనం – 1లో p = 2). అందువలన a మరియు b లకు 2 ఒక సామాన్య కారణాంకం అయినది.

a, b లు పరస్పర ప్రధానాంకాలు మరియు 1 తప్ప వీటికి ఎటువంటి ఉమ్మడి కారణాంకాలు లేనందున మనం ప్రతిపాదించిన ‘√2 అనేది అకరణీయం అనే భావన విరుద్ధతకు దారి తీస్తుంది. అందుచే √2 అనేది ” కరణీయ సంఖ్యగా నిరూపించవచ్చును.

ప్రశ్న 8.
5 – √3 ని ఒక కరణీయ సంఖ్య అని నిరూపించండి. (పేజీ నెం. 15)
సాధన.
మనం నిరూపించాల్సిన భావనకు విరుద్ధంగా, 5 – √3 ని ఒక అకరణీయ సంఖ్యగా ఊహించండి.
అంటే 5 – √3 = \(\frac{a}{b}\) ఇందులో a, b లు పరస్పర ప్రధానాంకాలు మరియు b ≠ 0.
కావున 5 – \(\frac{a}{b}\) = √3
సమీకరణంను తారుమారు చేస్తే, మనకు √3 = 5 – \(\frac{a}{b}=\frac{5 b-a}{b}\) అని వస్తుంది.
a, b లు పూర్ణ సంఖ్యలు కావున మనకు 5 – \(\frac{a}{b}\) ఒక అకరణీయ సంఖ్య అవుతుంది. కావున √3 కూడా, అకరణీయ సంఖ్యయే అగును. ఇది అసత్యం.
ఎందుకంటే √3 అనేది ఒక కరణీయ సంఖ్య.
ఈ భావన ఏర్పడటానికి, మనం ఊహించిన ప్రతిపాదన 5 – √3 ఒక అకరణీయ సంఖ్య అనే భావన తప్పు. అంటే ఇది ఒక విరోధాభాసం.
∴ 5 – √3 అనేది కరణీయ సంఖ్య అని మనం చెప్పవచ్చును.

ప్రశ్న 9.
3√2 అనేది ఒక కరణీయ సంఖ్య అని నిరూపించండి.(పేజీ నెం. 15)
సాధన.
మనం నిరూపించవలసిన భావనకు విరుద్ధంగా 3√2 అనేది ఒక అకరణీయ సంఖ్యగా ఊహించండి. a, bలు పరస్పర ప్రధాన సంఖ్యలు మరియు b ≠ 0 అయ్యేటట్లు 3√2 = \(\frac{a}{b}\) అవుతుంది.
క్రమంలో అమర్చగా, మనకు √2 = \(\frac{a}{3 b}\) అని వస్తుంది.
ఇందులో 3, a మరియు b లు పూర్ణసంఖ్యలు కావున \(\frac{a}{3 b}\) అనేది ఒక అకరణీయ సంఖ్య. అందుచే √2 కూడా ఒక అకరణీయ సంఖ్య అవుతుంది. ఇది అసత్యం. ఎందుకంటే √2 ఒక కరణీయ సంఖ్య అనే సత్యానికి విరుద్ధభావన అందుచే ఇది ఒక విరోధాభాసం. కావున మనం 3√2 అనేది కరణీయ సంఖ్య . అని చెప్పవచ్చును.

ప్రశ్న 10.
√2 +√3 అనేది ఒక కరణీయ సంఖ్య అని నిరూపించండి. (పేజీ నెం. 15)
సాధన.
√2 + √3 అనేది ఒక అకరణీయ సంఖ్య అని ఊహించండి.
√2 + √3 = 2, ఇందు a, b లు పూర్ణసంఖ్యలు మరియు b = 0 అని తీసుకోండి.
కావున, √2 = \(\frac{a}{b}\) – √3 అగును. ఇరువైపులా వర్గం చేయగా, మనకు
2 = \(=\frac{a^{2}}{b^{2}}\) + 3 – 2\(\frac{a}{b}\) √3 వచ్చును
క్రమంలో అమర్చగా.
2\(\frac{a}{b}\) √3 = \(=\frac{a^{2}}{b^{2}}\) + 3 – 2 = \(=\frac{a^{2}}{b^{2}}\) + 1
అంటే √3 = \(\frac{a^{2}+b^{2}}{2 a b}\)
a, b లు పూర్ణసంఖ్యలు కావున, \(\frac{a^{2}+b^{2}}{2 a b}\) ఒక అకరణీయ సంఖ్య. ఇదేవిధంగా √3 కూడా ఒక అకరణీయ సంఖ్య అవుతుంది. ఇది అసత్యం. ఎందుకంటే √3 అనేది ఒక కరణీయ సంఖ్య అనే సత్యానికి విరుద్ధభావన. ఇది ఒక విరోధాభాసం. కావున √2 + √3 అనేది ఒక కరణీయసంఖ్య అగును.

ప్రశ్న 11.
log \(\frac{343}{125}\) ను విస్తరించండి. (పేజీ నెం. 21)
సాధన.
log_a \(\frac{x}{y}\) = log_a x – log_a y అని మనకు తెలుసు.
∴ log \(\frac{343}{125}\) = log 343 – log 125
= log 7³ – log 5³
= 3 log 7 – 3 log 5
= 3[log 7 – log 5]

రెండవ పద్ధతి :
log \(\frac{343}{125}\) = log \(\left[\frac{7}{5}\right]^{3}\)
log_a xⁿ = n log_a x అని మనకు తెలుసు.
దీని నుండి
log \(\left[\frac{7}{5}\right]^{3}\) = 3 log \(\frac{7}{5}\)
= 3[log 7 – log 5]

ప్రశ్న 12.
2 log 3 + 3 log 5 – 5 log 2 ను ఒకే సంవర్గమానంగా రాయండి. (పేజీ నెం. 22)
సాధన.
2 log 3 + 3 log 5 – 5 log 2 ను ఒకే సంవర్గమానంగా వ్రాయుట.
2 log 3 + 3 log 5 – 5 log 2
= log 3² + log 5³ – log 2⁵
= log 9 + log 125 – log 32
= log (9 × 125) – log 32 [∵ log m + log n = log mn]
= log 1125 – log 32
= log 125 [∵ log m – log n = logm)

ప్రశ్న 13.
3^x = 5^{x – 2} సమీకరణాన్ని సాధించండి. (పేజీ నెం. 22)
సాధన.
3^x = 5^{x – 2} సంవర్గమాన రూపంలో వ్రాయగా
x log₁₀ 3 = (x – 2) log₁₀ 5
⇒ x log₁₀ 3 = x log₁₀ 5 – 2 log₁₀ 5
⇒ 2 log₁₀ 5 = x log₁₀ 5 – x log₁₀ 03
= x [log₁₀ 5 – log₁₀ 3]
∴ x = \(\frac{2 \log _{10} 5}{\log _{10} 5-\log _{10} 3}\)

ప్రశ్న 14.
2 log 5 + \(\frac{1}{2}\) log 9 – log 3 = log x అయితే x విలువను కనుగొనండి. (పేజీ నెం. 22)
సాధన.
2 log 5 + \(\frac{1}{2}\) log 9 – log 3 = log x అయిన ,x విలువ కనుగొనుట.
log x = 2 log 5 + \(\frac{1}{2}\) log 9 – log 3
= log 5² + log 9^{\(\frac{1}{2}\)} – log 3
= log 25 + log √ 9 – log 3
= log 25 + log 3 – log3
log x = log25
∴ log x = log25
⇒ x = 25 అగును.