AP Board 10th Class Maths Solutions Chapter 10 క్షేత్రమితి Exercise 10.3

SCERT AP 10th Class Maths Textbook Solutions Chapter 10 క్షేత్రమితి Exercise 10.3 Textbook Exercise Questions and Answers.

AP State Syllabus 10th Class Maths Solutions 10th Lesson క్షేత్రమితి Exercise 10.3

ప్రశ్న 1.
ఒక ఇనుప స్థూపాకార స్థంభము 2.8. మీటర్ల ఎత్తు, 20 సెం.మీ వ్యాసము కల్గియున్నది. దానిపై 42 సెం.మీ. ఎత్తు గల శంఖువు ఆకార భాగమున్నది. ఒక ఘనపు సెం.మీ. ఇనుము యొక్క బరువు 7.5 గ్రాములు అయితే ఆ ఇనుప స్థంభము యొక్క బరువు ఎంత?
సాధన.
ఇచ్చినవి : స్థూపం యొక్క వ్యాసార్ధం (r) = \(\frac{d}{2}\)
⇒ r = \(\frac{20}{2}\) = 10 సెం.మీ. ఎత్తు (h) = 2.8 మీ.
= 2.8 × 100 సెం.మీ. = 280 సెం.మీ.
శంఖువు యొక్క వ్యాసార్ధం r = \(\frac{d}{2}\)
= \(\frac{20}{2}\) = 10 సెం.మీ.
ఎత్తు (h) = 42 సెం.మీ.

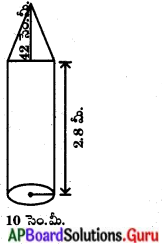
∴ ఇనుప స్థూపాకార స్థంభం యొక్క ఘనపరిమాణం = స్థూపం యొక్క ఘనపరిమాణం + శంఖువు ఆకార ఘనపరిమాణం
= πr²h + \(\frac{1}{3}\) πr²h
= (\(\frac{22}{7}\) × 10 × 10 × 280) + (\(\frac{1}{3}\) x \(\frac{22}{7}\) × 10 × 10 × 42)
= 88000 + 4400 = 92400 సెం.మీ³.
∴ 1 సెం.మీ³కు 7.5 గ్రా. చొప్పున ఇనుప స్థూపాకార స్థంభం యొక్క బరువు = 92400 × 7.5 = 693000 గ్రా.లు.
= \(\frac{69300}{1000}\) కి.గ్రా.
= 693 కి.గ్రాలు.

ప్రశ్న 2.
ఒక అర్ధగోళము యొక్క సమతల ఉపరితలముపై క్రమవృత్తాకార శంఖువు ఆకార భాగము యొక్క వృత్తాకార భూభాగము కలుపబడి యున్నట్లు ఒక ఆటవస్తువు ఉన్నది. శంఖువు ఆకార భాగము యొక్క భూవ్యాసార్ధము 7 సెం.మీ. మరియు దాని ఘన పరిమాణము అర్ధగోళాకార భాగము యొక్క ఘన 3 పరిమాణమునకు, రెట్లు ఉన్నది. శంఖువు ఆకార భాగము యొక్క ఎత్తు, మరియు ఆటవస్తువు యొక్క ఉపరితల వైశాల్యమును రెండు దశాంశ స్థానములకు సవరించి కనుగొనుము. (π = 3\(\frac{1}{7}\))
సాధన.

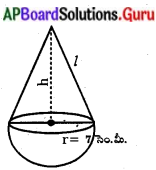
ఇచ్చినవి :
శంఖువు ఆకార పాదభాగ / అర్ధగోళం
యొక్క వ్యాసార్ధం = 7 సెం.మీ.
లెక్క ప్రకారం,
శంఖువు ఘనపరిమాణం = \(\frac{3}{2}\) × అర్ధగోళ ఘనపరిమాణం
⇒ \(\frac{1}{3}\) πr²h = \(\frac{3}{2}\) × \(\frac{2}{3}\) πr³
⇒ \(\frac{h}{3}\) = r (లేదా) \(\frac{h}{3}\) = 7
⇒ h = 21 సెం.మీ.
∴ శంఖువు ఆకార భాగం ఎత్తు (h) = 21 సెం.మీ.
ఆట వస్తువు యొక్క ఉపరితల వైశాల్యం = శంఖువు ఉపరితల/వక్ర వైశాల్యం + అర్ధగోళం ఉపరితల/వక్ర వైశాల్యం
= πrl + 2πr²
[∵ l = \(\sqrt{\mathrm{r}^{2}+\mathrm{h}^{2}}=\sqrt{7^{2}+21^{2}}=\sqrt{490}\) = 7√10]
= πr (l + 2r)
= \(\frac{22}{7}\) × 7 (7√10 + 2 × 7)
= 22 (7 × 3.162 + 14) [∵ √10 = 3.162]
= 22[22.134 + 14] = 22 × 36.134
= 794.948 చ.సెం.మీ. = 795 చ.సెం.మీ.

ప్రశ్న 3.
7 సెం.మీ భుజముగా గల ఘనము నుండి ఏర్పరచ గలిగే క్రమవృత్తాకార శంఖువు ఆకార వస్తువు యొక్క గరిష్ఠ ఘనపరిమాణము ఎంత ?
సాధన.

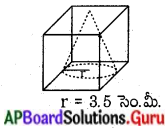
ఇచ్చినవి :
ఘనం యొక్క భుజం పొడవు = శంఖువు యొక్క ఎత్తు (h) = 7 సెం.మీ.
శంఖువు వ్యాసార్ధం (r) = 3.5 సెం.మీ.
[∵ r = \(\frac{\mathrm{d}}{2}=\frac{7}{2}\) = 3.5]
∴ ఘనంలో ఏర్పర్చగలిగే క్రమ వృత్తాకార శంఖువు ఆకార వస్తువు యొక్క గరిష్ఠ పరిమాణం (V) = \(\frac{1}{3}\) πr²h
= \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3.5 × 3.5 × 7
= \(\frac{22 \times 12.25}{3}=\frac{269.5}{3}\)
= \( 89.8 \overline{3}\)
V = 89.83 ఘ. సెం.మీ.

ప్రశ్న 4.
ఒక స్థూపాకార తొట్టె 5 సెం.మీ. వ్యాసార్ధము మరియు 9.8 సెం.మీ. పొడవును కల్గి నీటితో పూర్తిగా నింపబడి యున్నది. అర్ధగోళముపై నిటారుగా నిలుపబడిన క్రమ వృత్తాకార శంఖువు ఆకారములో యున్న ఘనాకార వస్తువు దానిలో ముంచబడినది. అర్ధగోళము యొక్క వ్యాసార్ధము 3.5 సెం.మీ. అర్ధగోళము బయట ఉన్న శంఖువు ఎత్తు 5 సెం.మీ. అయినచో తోట్టెలో మిగిలియున్న నీటి ఘనపరిమాణమును కనుగొనుము. (π = \(\frac{22}{7}\) గా తీసుకొనుము).
సాధన:

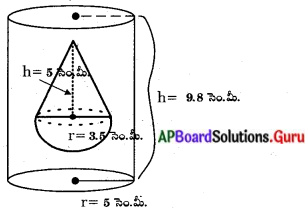
ఇచ్చినవి :
పై పటం నుండి స్థూపాకార తొట్టె యొక్క వ్యాసార్ధం = 5 సెం.మీ.
ఎత్తు = 9.8 సెం.మీ.
అర్ధగోళంపై నిటారుగా నిలబడిన శంఖువు ఎత్తు (b) = 5 సెం.మీ.
వ్యాసార్ధం (r) = 3.5 సెం.మీ.
స్థూపాకార తొట్టెలో మిగిలియున్న నీటి ఘనపరిమాణం = స్థూపాకార తొట్టె ఘనపరిమాణం – (శంఖువు ఆకార మరియు అర్ధగోళాకారాల ఘనపరిమాణాల మొత్తం)
= πr²h – [\(\frac{1}{3}\) πr₁²h₁ – \(\frac{2}{3}\) πr₂²h₂]
= (\(\frac{22}{7}\) × 5 × 5 × 9.8) – (\(\frac{2}{3}\) × \(\frac{22}{7}\) × 3.5 × 3.5 × 5 + × × (3.5)³)
= 770 – [64.16 + 89.83]
= 770 – (153.9)
= 770 – 154 [∵ 153.9 = 154]
= 616 ఘ. సెం.మీ.

ప్రశ్న 5.
ప్రక్క పటములో చూపిన విధముగా ఒక ఘనాకార 4 సెం.మీ. స్థూపము యొక్క రెండు చివరల నుండి 3 సెం.మీ శ్రీ వ్యాసార్ధము, 4 సెం.మీ ఎత్తు కల్గిన సమానముగా ఉన్న రెండు శంఖాకార భాగములు తొలగించబడినవి. స్థూపము యొక్క ఎత్తు 10 సెం.మీ., దాని వ్యాసం 7 సెం.మీ. అయినచో మిగిలిన భాగము యొక్క ఘనపరిమాణము ఎంత ?

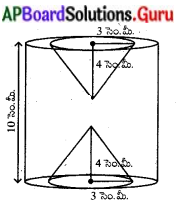
సాధన.
ఇచ్చినవి :
పై పటం నుండి ఘనాకార స్థూపం యొక్క ఎత్తు (h) = 10 సెం.మీ.
వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}=\frac{7}{2}\) = 3.5 సెం.మీ.
ఘనాకార స్థూపం నుండి తొలగింపబడిన శంఖువుల వ్యాసార్ధం (r) = 3 సెం.మీ.
ఎత్తు (h) = 4 సెం.మీ.
∴ ఘనాకార స్థూపం రెండు చివరల నుండి రెండు సమాన ఘనపరిమాణం గల రెండు శంఖువులను తోలగించగా మిగిలిన భాగం యొక్క ఘనపరిమాణం = ఘనాకార స్థూప ఘనపరిమాణం – 2 x శంఖువు ఘనపరిమాణం
= πr²h – [2 × \(\frac{1}{3}\) πr₁²h₁]
= \(\frac{22}{7}\) × 3.5 × 3.5 × 10 – [2 × \(\frac{1}{3}\) × \(\frac{22}{7}\) × 3 × 3 × 4]
= 110 × 3.5 – \(\frac{528}{7}\)
= 385 – 75.4 = 309.571 ఘ. సెం.మీ.

ప్రశ్న 6.
స్థూపాకార బీకరులో కొంత భాగము నీటితో నింపబడినది. బీకరు వ్యాసము 7 సెం.మీ. దానిలో 1.4 సెం.మీ. వ్యాసము కల్గిన గోళాకార చలువరాళ్ళు ఎన్ని వేస్తే దానిలో నీటి మట్టము 5.6 సెం.మీ. మేరకు పెరుగును ?
సాధన.

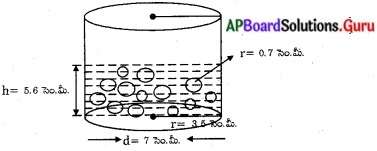
ఇచ్చినవి :
పై పటం నుండి స్థూపాకార బీకరు వ్యాసార్ధం (r) = \(\frac{\mathrm{d}}{2}=\frac{7}{2}\) = 3.5 సెం.మీ.
బీకరులో గోళాకార చలువరాళ్ళు వేస్తే దానిలోని నీటి మట్టం (h) = 5.6 సెం.మీ.
గోళాకార చలువరాళ్ళ వ్యాసార్ధం = \(\frac{\mathrm{d}}{2}\)
= \(\frac{1.4}{2}\) = 0.7 సెం.మీ.
∴ నీటి మట్టం బీకరులో 5.6 సెం.మీ.లు పెరగవలెనంటే దానిలో వేయవలసిన గోళాకార చలువరాళ్ళ సంఖ్య = (నీటి ఘనపరిమాణం) / (గోళం ఘనపరిమాణం)
= \(\frac{\pi r^{2} h}{\frac{4}{3} \pi r_{1}^{3}}\)
(‘.. నీరు పోసిన బీకరు స్థూపాకారంలో ఉంది)
= \(\frac{r^{2} h}{\frac{4}{3} r_{1}^{3}}=\frac{3.5 \times 3.5 \times 5.6}{\frac{4}{3} \times 0.7 \times 0.7 \times 0.7}\)

= \(\frac{\frac{35}{10} \times \frac{35}{10} \times \frac{56}{10} \times 3}{4 \times \frac{7}{10} \times \frac{7}{10} \times \frac{7}{10}}\)
4×7 x 10:17
= 5 × 5 × 2 × 3 = 25 × 6 = 150.

ప్రశ్న 7.
15 సెం.మీ. × 10 సెం.మీ. × 3.5 సెం.మీ కొలతలు కల్గిన దీర్ఘఘనములో 0.5 సెం.మీ. వ్యాసార్ధము మరియు 1.4 సెం.మీ. లోతుతో శంఖువు ఆకారం గల మూడు గోతులు తీసి పెన్ను స్టాండుగా మార్చారు. పెస్టాండ్ లోని కొయ్య ఘనపరిమాణము ఎంత ?

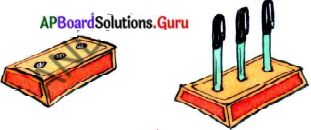
సాధన.
ఇచ్చినవి : 15 సెం.మీ. × 10 సెం.మీ. × 3.5
సెం.మీ.లు కొలతలు గల దీర్ఘఘనం ఘనపరిమాణం (V₁) = l × b × h (పొడవు × వెడల్పు × ఎత్తు)
= 15 × 10 × 3.5 = 525 ఘ. సెం.మీ.
శంఖువు ఆకార గోతుల వ్యాసార్థం (r) = 0.5 సెం.మీ.
లోతు (ఎత్తు) (h) = 1.4 సెం.మీ.
∴ 3 శంఖువు ఆకార గోతుల ఘనపరిమాణాల మొత్తం (V₂) = 3 × \(\frac{1}{3}\) πr²h
= πr²h
= \(\frac{22}{7}\) × 0.5 × 0.5 × 1.4
= 4.4 × 0.25
= 1.1 ఘ. సెం.మీ.
∴ పెన్ను స్టాండులోని కొయ్య ఘనపరిమాణం = మొత్తం కొయ్య ఘనపరిమాణం – 3 శంఖువుల గోతుల ఘనపరిమాణాల మొత్తం
= V₁ – V₂
= 525 – 1.1
= 523.9 ఘ. సెం.మీ.